План-схема уроку з математики "Числові вирази, рівності, нерівності"для учнів 5 класу.

Тема 1.	Натуральні числа.
Урок 13.	Числові вирази, рівності, нерівності.	5-Б клас	24.09.18
Класна робота	Перевірка виконання домашнього завдання: правила за § 4, с. 25-27: 1) що називають числовим виразом? 2) що називають числовою рівністю? 3) що називають числовою нерівністю? 4) якими бувають рівності та нерівності? 5) як порівнюють багатоцифрові числа? 6) як записують подвійну нерівність? перевірка завдань № 119, 121, 123, с. 30. Аналіз виконання учнями творчого завдання: № 127*(3), с. 31. Узагальнюючий відео-урок «Порівняння натуральних чисел». Практичне застосування знань: № 108, 116. Розв’язування складної нестандартної задачі: № 128, с.31.
Домашнє завдання	Довчити правила § 4, с. 25-27. Розв’язати № 109, № 117, № 129. Принести транспортир.

 

 

 

№ 108

Умова:

Запишіть числовий вираз та обчисліть його значення:
1) сума числа 152 та добутку чисел 45 і 21;
2) різниця суми чисел 245 і 197 та числа 45;
3) добуток суми чисел 452 і 148 та числа 12;
4) частка числа 625 та різниці чисел 100 і 75.

 Відповідь:

1) 152 + 45 • 21 = 152 + 945 = 1097: 
2) (245 + 197) - 45 = 442 - 45 = 397; 
3) (452 + 148) • 12 = 600 • 12 = 7200; 
4) 625 : (100 - 75) = 625 : 25 = 25.

№ 116

Умова:

На координатному промені (мал. 63) назвіть число, що розміщується: 1) на 5 одиниць лівіше від числа 5; 
2) на 4 одиниці правіше від числа 5; 3) між числами 5 і 12. Запишіть відповідні числові нерівності.

 Відповідь:

1) 5 - 5 = 0; точка 0; 0 < 5; 
2) 5 + 4= 9; точка 9; 9 > 5;
3) 5 < 8 < 12; точка 8; можуть бути і точки: 6; 7; 9; 10; 11.

 

№ 128

Умова:

Ганнуся купила 2 морозива та 1 тістечко і заплатила 35 грн/4 грн 50 к. Якби вона купила 1 морозиво та 2 тістечка, то заплатила б 40грн/6 грн. Скільки коштує морозиво і скільки коштує тістечко?

 Розв’язання:

2018

1) 35 + 40 = 75 (грн) — заплатила б Ганнуся за 3 морозива і 3 тістечка.
3) 75 : 3 = 25 (грн) — заплатила Ганнуся за 1 морозиво і 1 тістечко.
4) 35 - 25 = 10 (грн) — коштує морозиво. 
5) 40 - 25 = 15 (грн) — коштує тістечко.

Відповідь. Морозиво коштує 10 грн, а тістечко – 25 грн.

 

Розв’язання:

2013

1) 4 грн 50 к. = 450 к.; 6 грн = 600 к.
2) 450 + 600 = 1050 (к.) — заплатила б Ганнуся за 3 морозива і 3 тістечка.
3) 1050 : 3 = 350 (к.) — заплатила Ганнуся за 1 морозиво і 1 тістечко.
4) 450 - 350 = 100 (к.) — коштує морозиво. 
5) 350 - 100 = 250 (к.) — коштує тістечко.

Відповідь. Морозиво коштує 1 грн, а тістечко 2 грн 50 к.

 

Д/з

№ 129

Умова:

Старовинна задача. Торговець продав одному покупцеві 10 яблук, 5 груш і 3 лимони за 1 карбованець 10 копійок, другому покупцеві за тією самою ціною він продав 10 яблук, 3 груші і 1 лимон за 78 копійок, а третьому — 2 груші і 1 лимон за 22 копійки. Скільки коштують окремо яблуко, груша і лимон?

 

Розв’язання:

 

1) 1 карбованець 10 копійок = 110 к.

2) З перших двох покупців, яким торговець продав 20 яблук, 8 груш і 4 лимонів, він заробив 110 + 78 = 188 (к.).

3) Тоді за 5 яблук, 2 груші і 1 лимон торговець заробив 188 : 4 = 47 (к.).

4) Оскільки 2 груші і 1 лимон коштують 22 к., то 5 яблук коштують 47 - 22 = 25 (к.).

5) Отже, 1 яблуко коштує 25 : 5 = 5 (к.).

6) Тоді 3 яблука і 1 лимон коштують 78 — 10•5 = 28 (к.).

7) А 1 груша коштує 28 - 22 = 6 (к.).

8) Нарешті, 1 лимон коштує 22 - 2 • 6 = 10 (к.).
 

Відповідь. Яблуко коштує 5 к., груша — 6 к., а лимон — 10 к.

 

 

 

Д/з

№ 109

Умова:

Запишіть числовий вираз та обчисліть його значення:
1) сума добутку чисел 28 і 15 та числа 120;
2) добуток числа 35 та різниці чисел 506 і 468.

 

Відповідь:

1) 28 • 15 + 120 = 420 + 120 = 540; 
2) 35 • (506 - 468) = 35 • 38 = 1330.

№ 117

Умова:

На координатному промені (мал. 64) назвіть число, що розміщується:
1) на 4 одиниці правіше від числа 6;
2) між числами 6 і 11.
Запишіть відповідні числові нерівності.

  

Відповідь:

1) 6 + 4 = 10: точка 10; 10 > 6;
2) 6 < 8 < 11; точка 8; можуть бути і точки: 7; 9; 10.

Установити  відповідність між іменованими числами, що виражені різними одиницями виміру, так, щоб вони були рівними:

1. 27 кг 9 г;      А. 2079 кг;
2. 270 кг 90 г; Б. 27009 г;
3. 279 ц ;         В. 27 т 90 г;
4. 20 ц 79 кг;   Г. 2 т 7 кг 9 г;

                     Д. 27 т 900 кг.

 

 

Установити відповідність між нерівностями та цифрами, які можна в них поставити замість «*», щоб нерівності були вірними:

 

1.    50 6*5 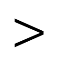50 685;                         А. 0;
2.    30 99* 999 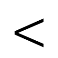30 992 000;           Б. 9;
3.    6 001 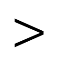600*;                               В. не можна

                                                            вставити

                                                                  жодну

                                                                  цифру;

4.    485 *10 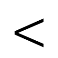485 410;                     Г. 0; 1;

                                                      Д. 0; 1; 2; 3.