Порадник для швидкого рахунку "Швидкий рахунок"

Пліщинська

загальноосвітнья школа І–ІІІ ступенів

 

 

 

 

 

 

 

 

2017

 

Укладач

Ніщук Ніна Іванівна,  вчитель математики, старший вчитель

 

 

 

 

Математика це наука яка захоплює. Сьогодні пропоную розглянути прийоми усних обчислень, які допоможуть прискорити і зробити більш зрозумілою процедуру математичних розрахунків, зроблених усно.

Точні обчислення без застосування спеціальних пристроїв істотно економлять час, дозволяють постійно тренувати свою пам’ять і, що приховувати, викликають інтерес у людей, що не наділені такими здібностями.

У більшості людей виникають труднощі при усному множенні двозначних чисел на однозначні. А про складні арифметичні розрахунки і говорити нічого.

Які ж способи найбільш ефективні, щоб навчитися якомога швидше усно множити двозначні числа?

Розглянемо традиційні методи, перевірені десятиліттями способи множення двозначних чисел, які не втрачають своєї актуальності.

 

Зміст

1. Цікавий спосіб множення "на пальцях"

1.1. Таблиця множення на 9

1.2. Множення на 6, 7 і 8

2. Графічні способи множення

2.1. Японський спосіб множення

2.2. Як множили єгиптяни?

2.3. Селянський спосіб множення

2.4. Староруський прийом множення двох чисел.

2.5. Індійський метод або метод решітки Аль-Хорезми

2.6. Спосіб " ПІРАМІДА "

2.8. Спосіб звернення та зсуву

3. Деякі способи швидкого множення

3.1. Множення натуральних чисел

3.2. Множення на 5

3.3. Множення на 4

3.4. Множення чисел на 11

3.5. Множення на 9, 99, 999

3.6. Множення на 15.

3.7. Способи множення на 25

3.8. Множення двозначних чисел, що закінчуються цифрою 5

3.9. Піднесення до квадрату числа, близького до 50

3.10. Множення двох чисел, близьких до 100

3.11. Множення чисел, що наближені до 100

3.12. Множення методом Ферроля

3.13. При множенні чисел з нулем в середині

3.14. Для множення двозначного числа на 101

1. Цікавий спосіб множення "на пальцях"

1.1. Таблиця множення на 9

Чи потрібно вчити таблицю множення? Діти цього, як правило, терпіти не можуть. І правильно роблять. Ні до чого її вчити! Але не поспішайте обурюватися. Ніхто не стверджує, що таблицю не потрібно знати. Її винахід приписують Піфагору, але, швидше за все, великий математик лише надав закінчену, лаконічну форму того, що вже було відомо. На розкопках стародавньої Месопотамії археологи знайшли глиняні таблички з сакраментальним: “2·2”. Люди давно користуються цією надзвичайно зручною системою обчислень і відкрили безліч способів, які допомагають осягнути внутрішню логіку і красу таблиці множення, зрозуміти – а не тупо, механічно зазубрити.

Математика – це наука «думаючого мозку» і вчити її потрібно, враховуючи, що існує безліч схем і алгоритмів для розв’язування того чи іншого питання.

У стародавньому Китаї таблицю починали вчити з множення на 9. Так простіше, і не в останню чергу тому, що множити на 9 можна “на пальцях”.

Розглянемо цей спосіб. Покладемо обидві руки на стіл долонями вниз. Позначимо перший зліва палець – 1, другий – 2 і т.д., як це показано. Щоб помножити довільне число від 1 до 9 на 9, подивимось на руки.

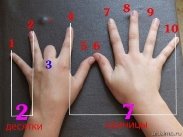Припустимо, що потрібно знайти добуток 9·3. Згинаємо палець, який відповідає числу, на яке множимо число 9 (тобто третій), рахуємо пальці до загнутого пальця (в нашому випадку – це 2), потім рахуємо пальці після загнутого пальця (в нашому випадку – 7). Пальці до загнутого означають десятки, після загнутого одиниці, тому отримали число 27.

1.2. Множення на 6, 7 і 8

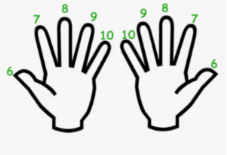Розглянемо спосіб, як помножити два числа від 6 до 10. Операція множення проводиться за такою схемою. Подумки пронумеруйте пальці рук наступним чином: повертаємо кисті рук лодонями до себе і позначимо кожен палець руки від 6 до 10  починаючи з мізинця.

Розглянемо множення 7·8.

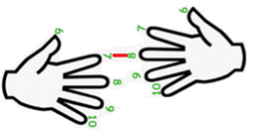Для цього з’єднаємо палець №7 лівої руки з пальцем №8 правої. А тепер порахуємо пальці: кількість пальців під з’єднанням (у нашому випадку 5) — це десятки.

Кількість пальців лівої руки, що залишилися зверху (разом з зєднанням), множимо на пальці, що залишилися зверху (разом з зєднанням) правої руки — це і буде число одиниць (3·2=6). Отже добуток чисел 7 і 8 дорівнює 56.

Якщо при множенні «одиниць» у результаті маємо число більше 9, то додаємо його десятки до попередніх десятків.

Це лише один з найпростіших прийомів “пальцевого” множення. Їх багато. “На пальцях” можна оперувати числами до 10 000!

У “пальцевої” системи є бонус: її можна сприймати як веселу гру. Охоче займаючись обчисленнями, отримуємо масу позитивних емоцій і в результаті швидко починаємо виконувати всі операції усно, без допомоги пальців.

2. Графічні способи множення

2.1. Японський спосіб множення

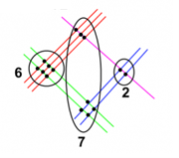Щоб множити багатоцифрові числа, пальців не достатньо, тому використовують графічний спосіб. Одним з таких є японський.

Розглянемо приклад 32·21.

На аркуші паперу по черзі малюємо лінії, кількість яких визначається за множниками прикладу.

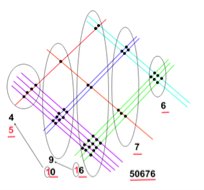Для множника 32 проводимо: 3 червоні лінії і трохи нижче – 2 сині. А для 21 перпендикулярно вже накресленним, проводимо спочатку 2 зелені, потім – 1 малинову. ВАЖЛИВО: лінії першого числа малюються в напрямку з верхнього правого кута в нижній лівий, другого числа – з нижнього правого, у верхній лівий. Потім рахуємо кількість точок перетину у кожній з трьох областей (на малюнку області позначені у вигляді кіл). Отже, в першій області (область сотень) – 6 точок, у другій (область десятків) – 7 точок, у третій (область одиниць) – 2 точки. Отже добуток  32·21 дорівнює 672.

Розберемо інший приклад: 123·412

Побудуємо лінії числа 123: 1 червону лінію і трохи нижче – 2 сині, і далі – 3 зелені. Потім числа 412: перпендикулярно вже накресленим, проводимо спочатку 4 фіолетових, потім 1 помаранчеву і 2 блакитних. За аналогією до попереднього прикладу, обводимо області перетинів колами. Всього їх вийшло 5, тому в результаті маємо п’ятизначне число. Знайдемо його: у першій області 4 точки перетину, у другій – 10, у третій – 16, в четвертій – 7 і в п’ятій – 6. Ті області, де кількість точок вийшло однозначною, складності не викликають, тому почнемо розбирати третю область, де 16 точок перетину: від числа 16 до цієї області залишаємо тільки останню цифру, тобто 6, все інше (тобто число 1) переносимо в сусідню область справа наліво, отже в третій області залишилося число 6, а в другій тепер до наявного числа 9 треба додати перенесену одиницю. Отже, у другій області тепер маємо число 10, і знову залишаємо 0 в другій області, а 1 перенесемо в першу. У першій стало на 1більше, тобто 5. Складемо цифри (переписуємо отриманий результат зліва направо) і одержимо число 50676, тобто  123·412=50676.

За допомогою цього способу можна множити будь-які числа, адже це просто, просто рахуєш точки перетину ліній.

Найважливіше - це правильно відокремити частини та переносити десятки.

2.2. Як множили єгиптяни?

Значення чисел, які використовувались у давнині, були більш або менш придатні для запису результату обрахунку. А ось виконувати дії з їхньою допомогою було дуже складно, особливо це стосувалось дії множення. Вихід з цієї ситуації знайшли єгиптяни, тому цей спосіб отримав назву єгипетський. Вони замінили множення на будь - яке число подвоєнням, тобто додаванням число з самим собою.

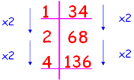Наприклад:    34·5=170

Єгиптяни замінили множення на будь-яке число -  подвоєннямм. Так як 5 = 4 + 1, то для отримання результату  залишилось додати числа, які стоять в правому стовбці напроти чисел 4 і 1, тобто  136 + 34 = 170.

2.3. Селянський спосіб множення

В Росії серед селян деяких губерній був розповсюдженій спосіб, який не потребував знань всієї таблиці множення. Треба було лише вміти множити та ділити на 2. Цей спосіб отримав назву селянського (існує думка, що він бере початок з єгипетського).

Розділимо множники вертикальною лінією. Принцип цього способу полягає у тому, що ми лівий множник (відносно вертикальної лінії) ділимо на 2 і результат записуємо під даним множником. Правий множник множимо на 2 і результат записуємо під цим ним. Усі ці дії ми робимо поки у лівому стовпчику не вийде 1. Якщо ж ми ділимо і у нас залишається остача, то ми її відкидаємо, і записуємо число без остачі. Остання важлива дія у цьому способі, це викреслити ті рядки у яких зліва парне число. Потім додаємо не викреслені числа правого стовпчика.

Розглянемо приклад 45·37. Напишемо числа на аркуші і розділимо їх вертикальною лінією. Ліве число ділимо на 2, відкидаючи залишок, поки не отримаємо одиницю. Праве – множимо до тих пір, поки число рядків в стовпчику не зрівняли. Потім викреслюємо з ПРАВОГО стовпчика всі ті числа, навпроти яких у ЛІВОМУ стовпчику вийшов парний результат (у нашому випадку 37 + 148 + 296 + 1184 = 1665).

Отже, 45·37 = 1665.

2.4. Староруський прийом множення двох чисел.

Суть цього прийому полягає у тому, що один множник збільшували у двоє, а другий зменшували у двоє, поки один з них не дорівнював одиниці (другий множник – степінь числа 2).

Наприклад, 27 помножити на 16. Один співмножник ставим на початку одного стовпчика і подвоювали, а другий – на початку другого стовпчика і відповідно ділили навпіл доти, поки не отримали 1:

27                       16

54                       8

108                     4

216                     2

432                     1

2.5. Індійський метод або метод решітки Аль-Хорезми

Видатний арабський математик та астроном Абу Абдалах Мухаммед Бен Мусса аль - Хорезми у своїй книзі "Книга про індійські обчислення" вчений описав спосіб, який придуманий у Стародавній Індії, а пізніше названий „методом решітки”.

Для множення багатоцифрових чисел скористаюсь таким алгоритмом:

1. Накреслити таблицю n×n, в якій n клітинки по довжині та n по ширині.
2. Записати перший множник по довжині над таблицею, а інший по ширині справа від таблиці.
3. У клітинка запишемо результат множення даних чисел, на їх перетині відокремимо десятки та одиниці діагоналлю. Отримані цифри складемо по діагоналі, і отриманий результат можна прочитати по стрілці.

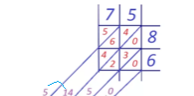
Розглянемо множення 75 та 86.

         6    4    5   0                                    

Хід виконання дій такий:

- малюємо прямокутник 2 на 2 (в нашому випадку двоцифрові числа)

- потім квадратні клітинки ділимо по діагоналі

- зверху таблиці записуємо число 75

- справа від таблиці записуємо число 86

- тепер в кожний квадратик впишемо добуток чисел - співмножників, розміщених на перетині стрічки та стовпчика, десятки вище діагоналі, одиниці нижче.

- результат записуємо внизу таблиці.

Отже, 75·86 = 6450                    

Аналогічно множимо трицифрове число на двоцифрове: 312·45.

1     4     0     4    0          

312·45 = 14040.     

 2.6. Спосіб " ПІРАМІДА "

Розглянемо множення числа 351 на число 248 за таким алгоритмом:

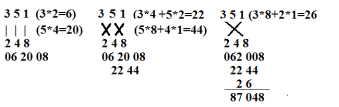1. Спочатку ми овинні записати це множення в стовпчик, потім треба помножити усі числа які стоять один під одним, виділяючи під кожний результат по 2 знака.

2. Після цієї дії просто множимо навхрест сусідні цифри. Разом пишемо зі зсувом на один знак вліво під результатом одного кроку.

3. Рохсуваємо крок хреста на 1 позицію. Під нього попадають тільки крайні цифри. Далі записуємо їхній добуток під результатом попереднього кроку зі зсувом на 1 знак вліво.

Для чисел більшої значності схема виглядає аналогічно.

 

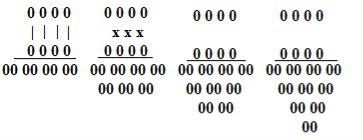
2.8. Спосіб звернення та зсуву

Виявляється, для цього досить розвернути один з множників навколо своєї молодшої цифри (переписати в оберненому порядку) і зсувати їх в такому вигляді один відносно другого, знаходячи суми добутків сусідів по вертикалі. Цей спосіб так и називається — спосіб зсуву, а працює він наступним чином.

Приклад. 35·54 перетворимо як 53·54

Проводимо розрахунки:                                                                                                    

 

 

 

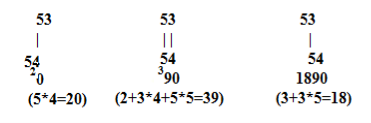
Не забудьте, що вибраний вами множник повертають навколо самої молодшої цифри!

3. Деякі способи швидкого множення

Існують маловідомі математичні прийоми, що дозволяють швидко і ефективно виконувати усно множення складних чисел.

3.1. Множення натуральних чисел

Для швидкого множення натуральних чисел можна використовувати розподільний та сполучний закони відносно додавання чи віднімання.

Розглянемо застосування цих законів.

9·419=9· (400+10+9)=9·400+9·10+9·9=3600+90+81=3771

7·194=7· (200–6)=7·200–7·6=1400–42=1358

Найбільш легким способом, як швидко навчитися усно множити великі числа, є перемножування десятків і одиниць. Спочатку множаться десятки двох чисел, потім по черзі одиниці і десятки. Чотири отриманих числа додаються.

Для використання цього методу важливо вміти запам’ятовувати результати множення і складати їх усно.

Розглянемо множення 38 на 57, для цього необхідно:

1. Розкладемо множники на суму двох доданків (30+8)·(50+7);
2. 30·50 = 1500 – запам’ятати цей результат;
3. 30·7 + 50·8 = 210 + 400 = 610 – запам’ятати цей результат;
4. (1500 + 610) + 8·7 = 2110 + 56 = 2166

Застосовуючи сполучний закон, легко обчислювати добутки чисел, якщо одне з них парне, а інше легко приводиться до числа з нулями (у нашому випадку 125):
32·125 це 16·250 це 8·500 це 4·1000 = 4000

Тобто одне з них зменшуємо у 2 рази, а інше збільшуємо у 2 рази. При цьому отримуємо рівність: 32·125=16·250=8·500=4·1000 = 4000.

Якщо ж це не так важко, то чому б не навчитися таким обрахункам.

3.2. Множення на 5
Для більшості людей множення на 5 не складає труднощів для невеликих чисел. Щоб швидко порахувати великі числа, помножені на 5 потрібно взяти це число і розділити на 2. Якщо результат – ціле число, то додайте до нього 0 в кінці, якщо немає, відкиньте залишок і додайте 5 в кінці:
1248·5 = (1248/2) _ (0 або 5) = 624_ (0 або 5) = 6240 (результат ділення на 2 ціле число)
4469·5 = (4469/2) _ (0 або 5) = (2234.5) _ (0 або 5) = 22345 (результат ділення на 2 число з залишком)

Або щоб помножити число на 5, треба його помножити спочатку на 10, а потім поділити на 2.

Наприклад :

138·5 = ( 138·10 ) : 2 = 1380 : 2 = 690

548·5 = ( 548·10 ) : 2 = 5480 : 2 = 2740

Щоб помножити число на 5, 25 чи 125 можна поділити його на 2, 4, 8 відповідно і в результаті помножити на 10, 100, 1000. Наприклад:

46·5=46:2·10=230

48·25=48:4·100=1200

32·125=32:8·1000=4000.

Якщо множник не ділиться націло на 2, 4, 8 , то ділення буде з остачею. Тому частку слід помножити на 10, 100, 1000, а остачу на 5, 25, 125. Наприклад:

53·5=26·10+1·5=265

43·25=10·100+3·25=1000+75=1075

66·125=8·1000+2·125=8000+250=8250

3.3. Множення на 4
Це дуже проста і, з першого погляду, очевидна фішка множення будь-якого числа на 4 – щоб просто помножити будь-яке число на 4, потрібно помножити його на 2, а потім знову помножити на 2:
67·4 = 67·2·2 = 134·2 = 268

214·4 = (214·2)·2 = 428·2 = 856

537·4 = (537·2)·2  = 1074·2 = 2148

Або 58·4 = (58·2) + (58·2) = (116) + (116) = 232

3.4. Множення чисел на 11

Припустимо, нам потрібно помножити 12 на 11. Візьмемо двозначне число, яке потрібно помножити на 11 і уявимо між його двома цифрами місце, на яке запишемо суму його цифр: 1+2 =3. Одержимо число132, тобто 13·11=132.

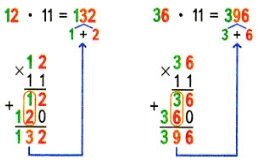Аналогічно, 36·11=396, оскільки 3+6=9.

Щоб помножити на 11 число, сума цифр якого 10 чи більше 10, треба подумки розсунути цифри цього числа, поставити поміж них суму цих цифр, та до першої цифри додати 1, а другу і останню (третю) цифру залишити без зміни.

59·11 = 649 (суму двоцифрового числа (5 + 9 = 14) перекидаємо одиницю вліво (5 + 1 = 6), так як сума більша 9. Цифру 4 записуємо в середину).
78·11 = 7 (7 + 8) 8 = 7 (15) 8 = 858;

94·11 = 9 (9 + 4) 4 = 9 (13) 4 = 1034.

79·11 = 869 (7_ (7 +9) _9 ;   (7 +1) _6_9)

Припустимо, нам потрібно помножити 124 на 11. Візьмемо число, яке потрібно помножити на 11 і уявимо між його першою і останньою цифрами місце, на яке запишемо суму його цифр починаючи з права на ліво: 2+4 =6 (сума одиниць і десяток числа 124) потім 1+2 =3 (сума десяток і сотень числа 124). Одержимо число1364, тобто 124·11=1364.

Аналогічно, 3765·11=41415

Щоб помножити двоцифрове число на 111, слід справа наліво записати послідовно останню цифру числа (тобто цифру з розряду одиниць), далі суму цифр числа, знову суму цифр числа і першу його цифру. Якщо сума цифр більша ніж 9, то записуємо цифру одиниць, а кожного наступного результату додаємо 1. Наприклад:

42·111==4662.

68·111==7548

Цікаві результати отримаємо в аналогічних добутках.

1·1 = 1
11·11 = 121
111·111 = 12321
1111·1111 = 1234321
11111·11111 = 123454321
111111·111111 = 12345654321
1111111·1111111 = 1234567654321
11111111·11111111 = 123456787654321
111111111·111111111 = 12345678987654321

Щоб помножити двоцифрове число на , можна спочатку його помножити на а, а потім на 11.

Щоб двохзначне число помножити на 22, 33, 44, 55, 66, 77, 88, 99, треба  цей множник подати у вигляді добутку однозначного числа на 11. Спочатку виконуємо множення на однозначне число, а потім на 11:

123·55=(123·5) ·11=615·11=6765

15· 33 = 15 · 3 · 11 = 45 · 11 =  495

23·  66 = 23· 6 · 11 = 138· 11= 1518

3.5. Множення на 9, 99, 999

Щоб помножити число на 9, 99, 999 можна до числа дописати стільки нулів, скільки дев’яток у другому множнику, а від результату відняти число. Наприклад:

286·9=2860–286=2860–300+14=2574

23·99=2300–23=2300–23=2277

18·999=18000–18=17982

3.6. Множення на 15.

Якщо число парне, то до числа додати його половину і приписуємо нуль:

38·

Якщо число не парне, то менше парне множимо на 15 і добавляємо 15: 3

1715=16.

Використовуючи дію множення на 15 розглянемо множення на 16.

1416=14

1916=19

Використовуючи дію множення на 15 розглянемо множення на 14.

1714=17

1814=18

3.7. Способи множення на 25

Щоб число помножити на 25, потрібно його помножити на 100 та поділити на 4. Розглянемо множення чисел 64

64

Та можна дію ділення на 4 розбити на дію ділення двічі на 2

Розглянемо добуток 348·25 = (348 · 100) : 4 = (34800 : 2) : 2 = 17400 : 2 = 8700

Можна скористатися і таким способом, якщо дане число не кратне 4, Щоб число помножити на 25, потрібно поділити його на 4, тоді остачу множимо на 25 і дописуємо до результату

Розглянемо добуток  66

Як наслідком з способу множення на 25, є множення на 26, тобто множимо на 25 і до результату додаємо саме число.

14= 350+14 = 364.

А також множення на 24, тобто множимо на 25 і від результату віднімаємо саме число.

1424 = 1425 –14 = 350 – 14 = 336.

3.8. Множення двозначних чисел, що закінчуються цифрою 5

Щоб помножити числа, запис яких закінчується цифрою 5 потрібно:

1. Помножити десяток першого числа та на 1 більший десяток другого числа.
2. Множимо одиниці цих чисел.
3.  По черзі записуємо добутки.

Розглянемо добуток 75·25.

Оскільки 7·3 (на 1 більше ніж десяток другого числа) =21 і 5·5=25, тоді 75·25=2125.

Як частковий випадок даного способу може бути піднесення чисел, що закінчуються цифрою 5 до квадрату.

Щоб піднести до квадрату число 85, яке закінчується цифрою 5 множимо число десятків 8 на наступне за ним число 8·9 = 72 і приписуємо 25

Отже, 85² = 7225.

Аналогічно 25² = 625, адже 2·3 = 6;   

Можна використати і інший спосіб, Щоб піднести до квадрату двозначне число, що закінчується на 5, то множимо першу цифру числа на саму себе плюс одиниця і додаємо в кінці 25.
Розглянемо число 45 в квадраті

45² = 4·(4 + 1) _25 = 2025

І іще один спосіб піднесення до степеня числа, що закінчується цифрою 5. Щоб помножити двоцифрове число, що закінчується на 5 саме на себе, слід його спочатку округлити до десятків з надлишком, а потім з недостачею, результати округлень перемножити і до добутку додати 25.

Розглянемо квадрат числа 85

85² = 90·80+25=7200+25=7225

3.9. Піднесення до квадрату числа, близького до 50

Виконуємо такі дії:

1. Віднімаємо з даного числа 25.
2. Дописуємо до різниці двоцифровим число квадрат надлишку до 50 (недостачі до 50).

Розглянемо квадрати чисел 58 та 48.

58² = 3364 (58 – 25 =33, 8² = 64, де 8 надлишок).

48² = 2304 (48 – 25 = 23, 2² = 4 (запишемо двоцифровим числом 04), де 2 недостача).

3.10. Множення двох чисел, близьких до 100

Позначимо ці числа: х = 100 – а  та  у = 100 – b, тоді

ху = (100 – а)(100 – b) = 100² – 100b – 100 а + аb = 100(100 – а – b) + аb = 100(х – b) + аb = 100(у – а) + аb.

Наприклад помножимо числа 93 та 92:

93·92 = (100  – 7)(100 – 8) = 8556

93 – 8 = 85 або 92 – 7 = 85, тоді 7·8 = 56, записуємо результат до різниці дописуємо добуток.

99·92 = (100 – 1)(100 – 8) = 9108

99 – 8 = 91 або 92 – 1 = 91, тоді 1·8 = 8, оскільки число в результаті чотиризначне, то добавляємо нуль.

Потрібно знайти їх різницю з сотнею (це 6 і 7). Тоді від першого числа відняти різницю з сотнею другого і записати попереду (94 – 7=87). Далі дописуємо добуток різниць (6.

Або обчислення по формулі (а+в)(а–в) = а²–в²

Нехай потрібно виконати усно множення 52·48.  Подумки перетворюємо ці множники на (50 + 2) · (50 – 2) і  використовуємо вказану формулу  (50 + 2)(50 - 2) = 50² – 2² = 2500 – 4 = 2496.

Подібним чином виконують і в інших випадках, коли один множник зручно представити в вигляді суми двох чисел, а другий в виді різниці тих же чисел

69·71 = (70 – 1)(70 + 1) = 4900 – 1 = 4899

84·76 = (80 + 4)(80 – 4) = 80² – 4² = 6400 – 16 = 6384

Аналогічно множимо трицифрові числа, чотирицифрові числа і т.д.

3.11. Множення чисел, що наближені до 100

Нехай необхідно помножити 96 на 92, у яких доповнення до 100–4 і 8 відповідно. Віднімаємо від першого множника доданок другого множника (96–8=88), або від другого множника доданок першого (92–4=88), цей результат буде першими цифрами шуканого добутку, а останніми цифрами буде добуток цих доповнень (4·8=32), тобто 96·92=8832. Наприклад:

95·94==8920

Це правило можна застосувати під час множення чисел близьких до 1000.

3.12. Множення методом Ферроля

Також часто зустрічаються завдання на розклад числа. Тому розглянемо розклад числа. 

Нехай маємо двохзначне число , де  a кількість десятків, b-одиниць, тому =10a+b. Аналогічно, =100a+10b+c, де a,b,c кількість сотень, десятків, одиниць відповідно. Так можна розписати будь-яке натуральне число.

Що це нам дає? Знаючи це, можна навчитися легко (усно) множити (трицифрові, чотирицифрові...) числа, знаючи таблицю множення і вміти додавати невеликі числа.

Розглянемо множення двоцифрових чисел.

·=(10a+b)(10c+d)=bd+10 (ad+cb)+100 ac.

Розглянемо добуток чисел 53·68, кількість одиниць:  3·8=24, 4 одиниці і 2 піде до десятків, десятків: 5·8+3·6=40+18=58, 58+2=60, 0 – десятків і 6 сотень, сотень: 5·6=30, 30+6=36, 6 сотень і 3 тисячі. Тому, 53·68=3604.

Аналогічно виконується множення чисел 37·48, оскільки

1.              8·7=56, записуємо 6 пам’ятаємо 5,
2.              8·3+4·7+5=57, записуємо 7 пам’ятаємо 5,
3.              4·3+5=17, записуємо 17.

Отже, 37·48=1776.

Методом Ферроля легко множити числа від 10 до 20 . наприклад:

12·14=168, оскільки

1.              2·4=8,
2.              1·2+4·1=6
3.              1·1=1

Так само можна множити і трицифрове число на двоцифрове. Наприклад:

125·23=2875, оскільки

1.              3·5=15, записуємо 5 пам’ятаємо 1,
2.              (3·2+5·2)+1=17, записуємо 7, пам’ятаємо 1,
3.              (3·1+2·2)+1=8, записуємо 8,
4.              2·1=2, записуємо 2.

Розглянемо множення трицифрових чисел.

·=(100a+10b+c)(100d+10e+f)=cf+10(bf+ec)+100(af+be+dc)+1000(ae+bd)+10000cf.

Розглянемо добуток чисел 462·759, кількість одиниць:  2·9=18, 8 – одиниць,1 піде до десятків, десятки:  6·9+2·5=64, 64+1=65,  десятків 5 і 6 піде до сотень, сотень: 4·9+6·5+2·7=36+30+14=80, 80+6=86, 6 сотень 8 піде до тисяч, тисяч: 4·5+6·7=20+42=62, 62+8=70, 0 тисяч і 7 піде до  десятків тисяч, десятків тисяч: 4·7=28, 28+7=35, 5 десятків тисяч і 3 сотні тисяч. Отже, 462·759=350658.

Я наслідок є множення будь-яких двозначних чисел, якщо сума добутків десятків і одиниць та навпаки одноцифрове число

13·12=156 (множимо десятки 1·1=1 множимо  одиниці 3·2=6, потім перемножуємо одиниці на десятки і навпаки і добутки додаємо 1·2+3·1=5. Це число записуємо між цифрами добутків десятків і одиниць 156)

А також, множення будь-яких двозначних чисел, якщо сума добутків десятків і одиниць та навпаки двоцифрове число

34·26= ( перемножуємо десятки з десятками і одиниці з одиницями даних чисел 3·2=6, 6·4=24, потім перемножуємо одиниці на десятки і навпаки і добутки додаємо 4·2=8 і 3·6=18, тоді 18+8=26. Далі додаємо 2 до розряду десятків 6+2=8, число 6 до розряду десятків добутку одиниць 24+60=84. Допишемо отримані числа 884)

3.13. При множенні чисел з нулем в середині

=10712

=11448

11235

3.14. Для множення двозначного числа на 101

Треба просто записати число два рази: 34·101 = 3434.

Щоб помножити число на 1001, треба приписати до нього три нулі і додати вихідне число.

53·1001 = 53000 + 53 = 53053

461·1001=461000 +461=461461