Порівняння альтернативних алгоритмів розв'язання задачі.

Порівняння альтернативних алгоритмів розв'язання задачі

Що таке алгоритм розязування задач у Python?Алгоритм - це набір інструкцій для виконання певної задачі. Способів розв'язання задачі може бути багато, і кожен з алгоритмів має певну ефективність. Важливо не лише отримувати результативний розв'язок задачі, але й робити це максимально ефективно. Залежно від обраної стратегії, алгоритму рішення - можна це завдання виконувати швидше або повільніше. 

Порівняння альтернативних алгоритмів розв'язування задач. Порівняння альтернативних алгоритмів розв'язування задач - це процес вибору оптимального способу розв'язування задачі на основі властивостей алгоритмів та вхідних даних. При розробці програм може бути кілька можливих способів розв'язування задач, кожен з яких має свої переваги та недоліки.

Порівняння альтернативних алгоритмів розв'язування задач. У процесі порівняння альтернативних алгоритмів розв'язування задач можна звернути увагу на наступні параметри:- Часову складність: час, необхідний для виконання алгоритму при різних вхідних даних. Часова складність може бути вимірювана виконанням фрагментів коду в реальному часі, або математично - оцінюванням кількості операцій, виконуваних алгоритмом, які залежать від обсягу вхідних даних.- Просторову складність: обсяг пам'яті, необхідний для виконання алгоритму. Просторова складність може оцінюватися кількістю змінних, масивів або об'єктів, що використовуються в алгоритмі, в тому числі кількість байтів, що потрібні для збереження кожного з них.- Ефективність: співвідношення між часовою та просторовою складностями. Алгоритм, який має меншу часову та просторову складності при такому ж ефекті, вважається більш ефективним.

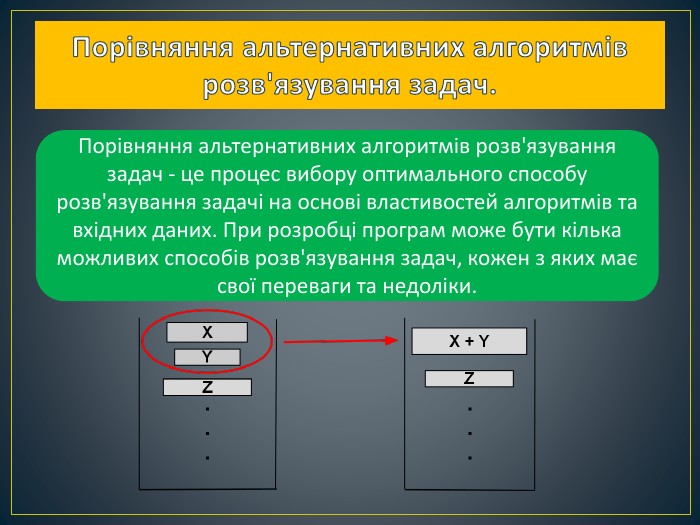
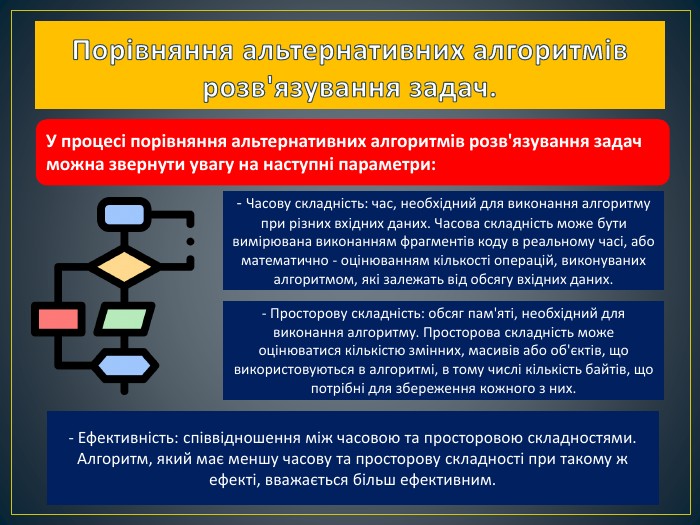
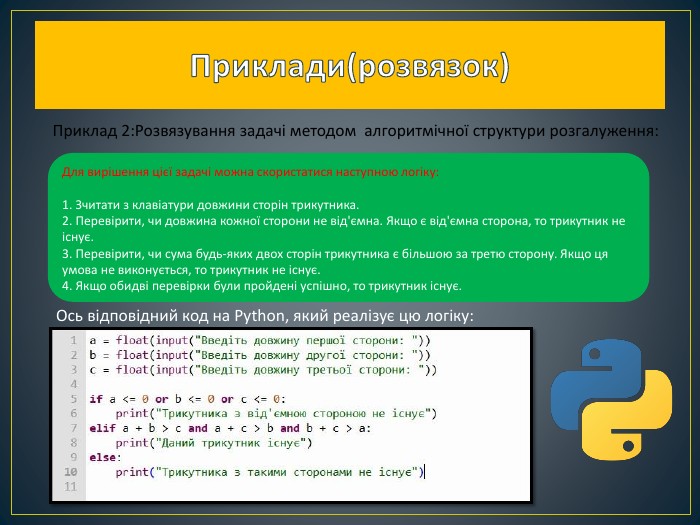
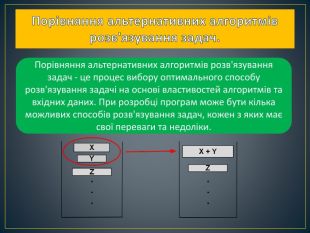
Порівняння альтернативних алгоритмів розв'язування задач. Продовження…- Надійність: здатність алгоритму працювати правильно та запобігати помилкам при різних вхідних даних. Різні алгоритми можуть здійснювати помилки при обробці певних видів даних або певних сценаріїв роботи програми. При проведенні порівняння альтернативних алгоритмів розв'язування задач на основі вищезазначених параметрів можна зробити висновок про найбільш оптимальний варіант. У процесі порівняння можуть виявлятися нові способи розв'язування задач, що можуть бути більш ефективними. Крім того, буває корисним перевіряти різні алгоритми при різних обсягах вхідних даних, щоб визначити ті, які дають найкращі показники в ході роботи програми.

Порівняння альтернативних алгоритмів розв'язування задач. Кожен алгоритм має свої переваги та недоліки, тому вибір правильного алгоритму залежить від розміру даних, типу даних, точності, ефективності та інших факторів. Тому, щоб вирішити задачу класифікації за допомогою машинного навчання в Python, необхідно вивчити кілька альтернативних алгоритмів та порівняти їх, щоб вибрати оптимальний для конкретних умов та завдань. Зазвичай час, необхідний алгоритмом, поділяється на три типи: -Найкращий варіант – мінімальний час, необхідний виконання програми. -Середній – середній час, необхідний виконання програми. -У найгіршому випадку – максимальний час, необхідний виконання програми.

Порівняння альтернативних алгоритмів розв'язування задач.Існують три основні (базові) алгоритмічні структури: слідування (лінійна), розгалуження та повторення, за допомогою поєднання яких може бути представлено логічну структуру будь-якого алгоритму. Пригадаємо

Приклади Задача 1. На вході маємо довжини сторін трикутника. Якщо даний трикутник може існувати, то на екрані виведеться повідомлення «Даний трикутник, існує», в іншому випадку «Трикутника з таки сторонами не і снує». Приклад 1: Розвязування задачі методом алгоритмічної структури повторення:1. Спочатку введемо довжини сторін трикутника та задамо початковий стан для змінної trykutnik_isnue:2. Після цього, запустимо цикл while, який буде продовжуватися, доки введені значення сторін не будуть у відповідності з умовою існування трикутника:

Приклади(розвязок)Кінцевий код програми:

Приклад 2: Розвязування задачі методом алгоритмічної структури розгалуження: Приклади(розвязок)Для вирішення цієї задачі можна скористатися наступною логіку:1. Зчитати з клавіатури довжини сторін трикутника.2. Перевірити, чи довжина кожної сторони не від'ємна. Якщо є від'ємна сторона, то трикутник не існує.3. Перевірити, чи сума будь-яких двох сторін трикутника є більшою за третю сторону. Якщо ця умова не виконується, то трикутник не існує.4. Якщо обидві перевірки були пройдені успішно, то трикутник існує. Ось відповідний код на Python, який реалізує цю логіку:

Приклади(розвязок)Задача 2. Клієнт банку поклав на депозит в банк 1000 гривень на n – ну кількість років. Річний відсоток становить 25%. Треба порахувати скільки грошей отримає користувач наприкінці періоду. Приклад 1: Розвязування задачі методом алгоритмічної структури повторення: У цій програмі ми використовуємо цикл `while`, щоб пройти через кожен рік депозиту. Кожного року ми додаємо відсотки до початкової суми депозиту за допомогою формули для простих процентів, де `depozit` - є початковою сумою депозиту, `ps` - є річним процентом, а `n` - є кількістю років депозиту. Після цього, в циклі збільшуємо значення `i` на 1, щоб перейти до наступного року. Нарешті, ми виводимо отриману суму за допомогою функції `print`.

Приклади(розвязок)Приклад 2: Розвязування задачі методом алгоритмічної структури слідування: У цьому коді змінні ` depozit `, `ps` і `n` встановлені відповідно до умови задачі. Значення `s` обчислюється за формулою складних процентів, яку ми використовували раніше. Результат обчислення виводиться на екран за допомогою функції `print`.

Дякую за увагу!