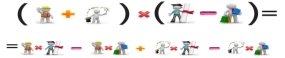Посібник для уроків алгебри ІІ семестр 7 класу (оновлений)
Дана розробка може бути використана як додаток до уроків алгебри у ІІ семестрі 7 класу, як роздатковий матеріал учням. Укладена згідно Комбінованої системи М.П. Гузика
Тема №4. Многочлени
Урок №1

Многочлени
Світ математики – це немовби багатоповерхова
будівля, причому ідеї кожного поверху зв’язані як між
собою, так і з тими, що знаходяться вище і нижче.
Г. Харді
Питання
- Многочлен.
- Дії над многочленами.
- Розкладання многочленів на множники.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §2, пункти 8 – 13, стор. 54 – 88.
|
||
|
1.1 |
Многочленом називають суму кількох одночленів. |
|
|
1.2 |
Многочлен, який є сумою одночленів стандартного вигляду, серед яких немає подібних членів, називають многочленом стандартного вигляду. |
|
|
1.3 |
Степенем многочлена стандартного вигляду називають найбільший із степенів одночленів, які утворюють даний многочлен. |
|
|
1.4 |
Подібні доданки многочлена називаються подібними членами многочлена. |
|
|
||
|
2.5 |
Щоб додати (відняти) многочлени, достатньо записати їх суму (різницю), розкрити дужки та звести подібні члени. |
|
|
2.6 |
|
|
|
2.7 |
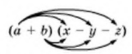
Щоб помножити многочлен на многочлен, досить кожний член одного многочлена помножити на кожний член іншого многочлена й одержані добутки додати.
|
|
|
||
|
3.8 |
Розкласти многочлен на множники означає подати його як добуток кількох многочленів. |
|
|
3.9 |
Щоб розкласти многочлен на множники способом винесення спільного множника за дужки, потрібно визначити спільний множник для усіх членів, а потім на основі розподільної властивості множення записати одержаний вираз у вигляді добутку. |
|
|
3.10 |
Щоб розкласти многочлен на множники способом групування, слід члени многочлена згрупувати так, щоб кожна група мала спільний множник. Після винесення в кожній групі спільного множника за дужки повинен утворитись спільний множник для всіх груп, який знову потрібно винести за дужки. |
|
Урок №2
«Мислить той, кому ставлять розумні запитання»
Народна творчість
Фронтальне опрацювання матеріалу
Многочлен. Подібні члени многочлена та їх зведення
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.4 блоку № 4.
- Усно дай відповідь на питання:
- Що називають многочленом?
- Який многочлен називається многочленом стандартного вигляду?
- Що називають степенем многочлена?
- Що таке подібні члени многочлена?
-
Що називають одночленом?
- Розглянь схему, розміщену на стор. 54 підручника.
- Усно виконай вправу 292, стор. 56 підручника.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово виконай вправи, стор. 56 – 57 підручника:
293 (1, 3, 4), 296, 298, 299, 304 (2, 4).
Урок №3
«Немає нічого небезпечнішого за підступного
ворога, але немає нічого отруйнішого від удаваного друга»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Додавання і віднімання многочленів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.5 блоку № 4.
- Усно дати відповідь на питання:
- Що називають многочленом?
- Який многочлен називається многочленом стандартного вигляду?
- Що називають степенем многочлена?
- Що таке подібні доданки многочлена?
- Як додати або відняти многочлени?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
2.1. Розгляньте правила зведення подібних доданків і запам’ятайте їх:
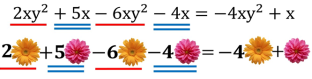
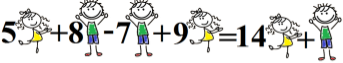
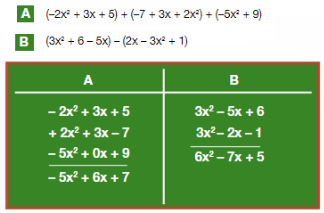
2.2. Виконати усно вправу, яка знаходиться за посиланням https://learningapps.org/6541699.
Завдання 3.
Письмово виконати вправи, стор. 59 – 60 підручника: 306, 307 (1, 3); 308 (1, 3), 311 (2, 4), 313 (3).
Завдання 3.
Складіть число, яке складається:
-
з
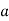 сотень,
сотень, 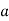 десятків та
десятків та 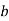 одиниць;
одиниць;
-
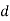 тисяч,
тисяч, 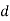 десятків та
десятків та 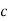 одиниць.
одиниць.
Уроки №4, 5
«Тоді лише пізнається
цінність часу, коли він утрачений»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Множення одночлена і многочлена
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.6 блоку №4.
- Усно дай відповідь на питання:
- Що називають многочленом?
- Який многочлен називається многочленом стандартного вигляду?
- Що називають степенем многочлена?
- Що таке подібні доданки многочлена?
- Як додати або відняти многочлени?
- Як помножити одночлен на многочлен?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
«Вгадай, хто це»
2.1. Спростіть вираз:
1) ![]() ;
;
2) ![]()
3) ![]()
4) -![]()
2.2. Спростіть вираз:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
|
|
|
|
|
|
|
|
|
|
|
г |
с |
к |
а |
с |
р |
у |
л |
а |
Завдання 3.
Письмово виконати вправи, стор. 66 – 67 підручника: 355 (1, 3, 5, 7, 9, 11); 357 (2, 4, 6, 8); 361 (1, 3, 5), 364, 374.
Завдання 4.
Гра на уважність.
Потрібно за 1 хв. знайти на малюнку 3 комашки сонечко і 3 усміхнених обличчя дитини.

Завдання 5.
5.1. Сьогодні ми дізнаємось про сім чудес України. Перші два чуда знаходяться у столиці України – Києві. Це Києво-Печерська лавра та Софія Київська.
5.2. Розгадайте кросворд, прочитайте ключове слово і ви дізнаєтеся назву міста у якому знаходиться ще одне з чудес України.
- Що зміниться у одночлена, якщо його помножити на (–1)?
- Як називається другий степінь ?
- Як називається добуток кількох рівних множників?
- Як називають суму кількох одночленів?
- Наслідком якого закону є правило множення многочлена на одночлен?
-
Який показник степеня отримаємо у виразі
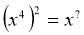 .
.
-
Який знак потрібно поставити замість ☼, щоб рівність була вірною
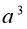 ☼
☼ 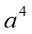 =
= 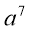 ?
?
- Що утворюють два тотожно рівних вирази, сполучені знаком рівності?
- Який коефіцієнт отримаємо, якщо зведемо подібні 23а4 – 12 а4 ?
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3. Із виразів, що містяться в стовпцях А і Б Таблиці 1 складіть правильні рівності, отримайте чотири двоцифрових числа. Утворені числа розмістіть у порядку зростання і за допомогою Таблиці 2 прочитайте закодоване слово.
Таблиця 1.
|
№п/п |
А |
Б |
№п/п |
|
1 |
(3а + с) 2а |
6х5 – 8х4 + 10х3 2 |
1 |
|
2 |
2х3 (3х2 – 4х + 5) |
– 6а5 + 8а4 4 |
2 |
|
3 |
(– а + ас)с2 |
6а2 + 2ас 1 |
3 |
|
4 |
–2а3(3а2 – 4а) |
– ас2 + ас3 3 |
4 |
Таблиця 2.
|
13 |
21 |
34 |
42 |
|
ХЕ |
РС |
ОН |
ЕС |
5.4. Одна сторона прямокутника в 4 рази більша за другу. Якщо меншу сторону збільшити на 3 см, то площа прямокутника збільшиться на 24см2. Знайдіть сторони прямокутника.
5.5. Складіть, будь-ласка, слово із букв, що визначають правильний варіант вашої відповіді і прочитайте назву міста.
- При якому т справедлива рівність а16 ат = а32 :
О. 2. Х. 16. Т. 1?
- Спростіть вираз (2а + 3в) + (7в – 3а) – (8а – 6в) .
Н. 13а – 4в. О. –9а + 16в. И. 7а – 16в.
- Знайдіть показник результату (а6 : а3)3.
Т. 9. У. 6. Б. 12.
- Розв’яжіть рівняння 2х2·х = – 2.
Х. 0. А. 1. И. – 1.
- При якому р справедлива рівність (а10)2 · (а5)4 = ар ?
Н. 40. О. 21. Я. 400.
5.6. Для зустрічі з сьомим дивом України вам потрібно розв’язати рівняння і розгадати зашифроване слово. Розмістіть відповіді до рівнянь у порядку спадання.
а) 3(2х – 5) + 7(3х – 4) = 3х + 77 б) 5(4 – 7х) – 3(5х + 1) = х – 85
в) 5(8у – 1) – 7(4у + 1) + 8(7 – 4у) = 19
г) 7(6z – 1) + 5(7 – 12z) + 3(1 + 2z) = 23
Шифр. 5 – У; 2 – М; 1,25 – А; ![]() – НЬ.
– НЬ.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Запишіть у вигляді многочлена число, яке складається з b сотень, b десятків і a одиниць.
-
Спростіть вираз

-
Запишіть у стандартному вигляді многочлен
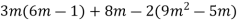
та знайдіть його значення, якщо ![]() .
.
-
Розв’яжіть рівняння:
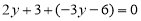 .
.
-
Розв’яжіть рівняння:
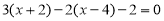 .
.
Уроки №7, 8
«Як хто посіє в юності, так пожне в старості»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Множення двох многочленів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 2.7 блоку № 4.
- Усно дати відповідь на питання:
- Що називається многочленом?
- Який многочлен називають многочленом стандартного вигляду?
- Що називають степенем многочлена стандартного вигляду?
- Що називається подібними членами многочлена?
- Як додати або відняти многочлени?
- Як помножити одночлен на многочлен?
-
Як помножити многочлен на многочлен?
- Виконати усно вправи, запропоновані вчителем у презентації.
- Запишіть у блок і запам’ятайте правило множення многочленів за допомогою символів.
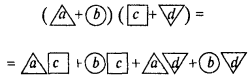
Завдання 2.
2.1. Виконати множення усно:
-
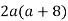 ;
;
-

-
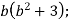
-
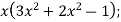
-
 ;
;
-
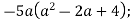
-
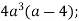
-
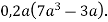
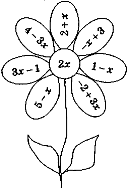
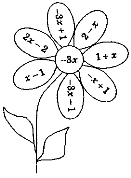
2.2. Помножити одночлен, записаний всередині квітки, на многочлени, які записані на її пелюстках.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи, стор. 72 – 73 підручника: 392 (1, 3, 7, 9, 11); 394 (2, 4); 396 (1); 398 (1, 3, 5).
Завдання 4.
Письмово виконати вправи, стор. 74 – 75 підручника: 401 (2, 4), 406, 410, 412 (1, 5), 416.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 5.
- «Дивись не помились» – дописати розв’язування вправи:
- « Знайди помилку»
![]()
Урок №9
«Хороша любов є та, яка є
істинною, міцною і вічною»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Розкладання многочлена на множники. Винесення спільного множника за дужки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 4.
- Усно відповісти на питання:
- Що називають многочленом?
- Як додати або відняти многочлени?
- Як помножити одночлен на многочлен?
- Як помножити многочлен на многочлен?
- Що означає розкласти многочлен на множники?
- Які є способи розкладання многочлена на множники?
- Як розкласти многочлен на множники способом винесення спільного множника за дужки?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розгляньте приклади 1, 2, 4 стор.77 – 78 підручника.
- Користуючись розглянутими прикладами, письмово виконайте вправи, стор.79 – 81 підручника: 433 (1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21); 435; 439 (1, 3, 5); 443 (1, 3, 5); 447 (1, 3, 5); 449 (2, 4).
- Клас ділиться на 3 групи.

Урок №10, 11
«Для всього свій час, і година своя кожній
справі під небом: час мовчати і час говорити»
Книга Еклезіаста 3: 1, 7
Фронтальне опрацювання матеріалу
Розкладання многочлена на множники способом групування
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 4.
- Усно відповісти на питання:
- Що називають многочленом?
- Як додати або відняти многочлени?
- Як помножити одночлен на многочлен?
- Як помножити многочлен на многочлен?
- Що означає розкласти многочлен на множники?
- Які є способи розкладання многочлена на множники?
- Як розкласти многочлен на множники способом винесення спільного множника за дужки?
-
Як розкласти многочлен на множники способом групування?
- Усно розв’язати вправи:
-
Позначте спільний множник для виразів
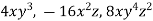 :
:
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажіть способи групування членів многочлена: а)
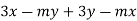 ; б)
; б) 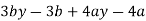 .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Знайдіть помилку у розв’язанні прикладів і наведіть правильну відповідь:
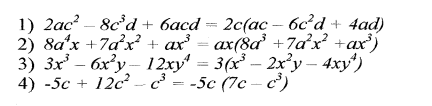
Завдання 3.
Знайдіть у правій колонці відповіді на приклади, записані у лівій колонці:
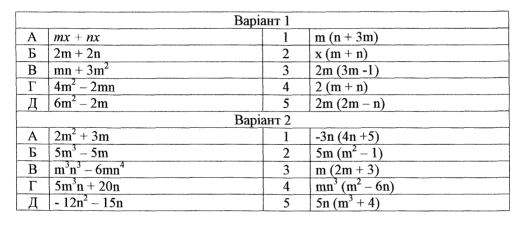
Завдання 4.
Письмово розв’язати вправи, стор. 85 – 86 підручника: 476 (1, 3, 7), 482 (1, 2).
Завдання 5.
Розкладіть многочлен на множники:
Завдання 6.
Усно виконати вправи, запропоновані вчителем у презентації.
Завдання 7.
Усно виконати вправи:
![]()
![]()
Завдання 8.
8.1. Письмово виконати вправи:


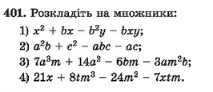
8.2. Робота в групах над завданням, запропонованим вчителем у презентації.
Урок №12
«Життя вимірюється не кількістю зроблених
вдихів і видихів, а кількістю тих моментів,
коли від щастя захоплює дух»
Фільм «Метод Хітча»
Фронтальне опрацювання матеріалу
Урок – квест «Вперед за козацькими скарбами»
Розкладання многочлена на множники
І. Робота над засвоєнням понять, термінів і правил
Слово «квест» означає: спортивно-інтелектуальне змагання, основою якого є послідовне виконання заздалегідь підготовлених завдань командами або окремими гравцями. Наш урок-квест буде тематичним, він буде проходити під гаслом «Вперед за козацькими скарбами!» І провести його мені допоможуть відомі вам із дитинства веселі та кмітливі козаки. Саме вони розповіли мені про козацькі скарби заховані на острові Хортиця.
Але спочатку познайомимося з правилами уроку-квесту.
Ви будете виконувати завдання, щоб мандрувати запропонованим маршрутом. Кожне правильно виконане завдання є ключем до наступного етапу подорожі. Виконавши спільними зусиллями усі завдання, ви знайдете козацькі скарби.
І пам’ятайте, що козацький скарб – не простий, і знайти його зможуть лише ті, хто має козацький дух, гострий розум та неабияку спритність.
Завдання 1.
- Повторити тези блоку №4.
- Карта острова перед вами на екрані, але щоб пройти на Січ, потрібно перевірити чи готові ви до подорожі. Дайте відповідь на питання:
- Що означає розкласти многочлен на множники?
- Скільки способів розкладання многочлена на множники ви знаєте?
- Як розкласти многочлен на множники способом винесення множника за дужки ?
- Як розкласти многочлен на множники групування?
Ви справились з 1-им завданням і отримуєте ключ від Січі.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Щоб дізнатись наступний етап маршруту, треба розгадати козацький кросворд.
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
Як називається представник вільних озброєних людей, які боронили Україну?
Як називається основна відзнака гетьманської влади та кошового отамана на Січі?
Хто в козацькому війську відповідав за написання важливих документів?
Яка улюблена страва козаків?
На якій ріці розташований острів Хортиця?
Хто очолював Військо Запорізьке?
Завдання 3.
Ви маєте нове завдання, щоб отримати наступну підказку щодо нашого маршруту, потрібно розв’язати таку головоломку.. На екрані буде висвітлено розв’язки і яка буква відповідає певному розв’язку. Розв’язавши всі завдання ви отримаєте нову підказку Розв’язки виконуємо у зошиті.
|
3a²-6a³= |
|
(x-y)²-3x(x-y)= |
|
6a-12c-ap+2cp= |
|
(a -2b)-3a(a-2b)= |
|
x³-14x²-2x+28= |
|
2x(x-4)-7(4-x)= |
|
3a²(1-2a) |
(x²-2)(x-14) |
(a-2c)(6-p) |
(2x+7)(x-4) |
(2-3a)(a-2b) |
(x-y)(-y-2x) |
Завдання 4.
Оберіть собі рівень і виконайте завдання у зошиті. Але знову всі рівняння повинні бути виконані. Я бачу, що козаки залишили нам пергамент із підказкою, це ребус. Корені рівнянь розшифрують ребус з підказкою.
|
Середній рівень |
Достатній рівень |
Високий рівень |
|
Розв’яжіть рівняння: y(y+2)-7(2+y)=0 |
Розв’яжіть рівняння: 3x2- 9x - x+3=0 |
Розв’яжіть рівняння: x³-5x²+x=5 |
Завдання 5.
Розв’язати задачу: Вирушивши у похід, козаки за 3 дні подолали 120 км. Другого дня вони проїхали 4/5 відстані, яку здолали першого дня, а третього – 20% цієї ж відстані. Скільки кілометрів долали козаки кожного дня?
Отримана правильна відповідь дає вам право сісти до козацького човна і доплисти до заключного етапу нашого квесту. Ось ми причалили до берега і бачимо тут під різними номерами об’єкти: старий дуб, ліс, млин, болото, висока могила. Де ж, на вашу думку, знаходиться козацький скарб?
Нагороди:
булава — відзнака гетьманської влади та кошового отамана на Січі;
бунчук — відзнака гетьмана і кошового, зберігалася у бунчужного;
корогва — військова відзнака, зберігалася у хорунжого;
печатка — зберігалася у генерального судді .
Та пам’ятайте, що тільки разом ці клейноди є справжнім скарбом. Так само і ви лише в єдності зможете досягти мети.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Перетворіть у многочлен: 1)
 ; 2)
; 2) 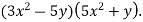
-
Розв’яжіть рівняння: 1)
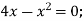 2)
2) 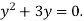
-
Розкладіть на множники: 1)
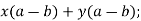 2)
2) 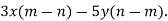
-
Розкладіть на множники методом групування: 1)
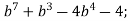 2)
2) 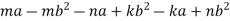 .
.
- Доведіть тотожність:
![]()
Урок №14
«Бери вершину i матимеш середину»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Многочлени
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 4 «Многочлени».
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Вкажіть многочлен стандартного вигляду:
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Спростіть вираз:
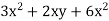 +7ху.
+7ху.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розкрийте дужки:
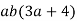 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконати вправи:
-
Розкрийте дужки і зведіть подібні доданки: 1)
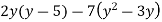 ; 2)
; 2) 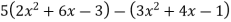 .
.
-
Розкладіть на множники: 1)
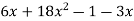 ; 2)
; 2) 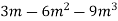 .
.
-
Доведіть, що для будь-якого цілого значення
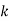 значення виразу
значення виразу 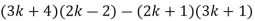 ділиться на 3.
ділиться на 3.
-
Розв’яжіть рівняння:
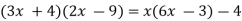 .
.
- Знайдіть чотири послідовних цілих числа, якщо добуток двох менших з них на 54 менший за добуток двох більших.
Тема №5. Формули скороченого множення
Урок №1

Формули скороченого множення
«У математики існує своя мова – це формули»
Софія Ковалевська
Питання
- Різниця квадратів двох виразів.
- Квадрат двочлена.
- Різниця і сума кубів двох виразів
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §2, пункти 15 – 19, стор. 93 - 131.
|
|||
|
1.1 |
Добуток різниці двох виразів та їх суми дорівнює різниці квадратів цих виразів. |
|
|
|
1.2 |
Різниця квадратів двох виразів дорівнює добутку різниці цих виразів та їх суми. |
|
|
|
|||
|
2.3 |
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу. |
|
|
|
2.4 |
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток цих виразів плюс квадрат другого виразу. |
|
|
|
|||
|
3.5 |
Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми. |
|
|
|
3.6 |
Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їх різниці. |
|
|
Урок №2
«Не достатньо мати лише добрий розум,
головне – це раціонально застосовувати його»
Р. Декарт
Фронтальне опрацювання матеріалу
Множення різниці двох виразів на їхню суму
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.2 блоку № 5.
- Усно дати відповідь на питання:
• Дайте означення многочлена.
• Який многочлен називають многочленом стандартного вигляду?
• Що називають степенем многочлена?
• Як помножити одночлен на многочлен ?
• Як помножити многочлен на многочлен?
• Що означає розкласти многочлен на множники?
• Які способи розкладання многочлена на множники вам відомі?
• Як розкладають многочлен на множники способом винесення спільного множника?
• Як розкладають многочлен на множники способом групування?
Завдання 2.
2.1. Піднесіть до квадрата вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.2. Подайте у вигляді квадрата вираз:
а) ![]() ; 6)
; 6) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Використовуючи формулу різниці квадратів
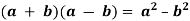 , спростіть дані вирази:
, спростіть дані вирази:
а![]() .... б)
.... б)![]() ....
....
в)![]() =.... г)
=.... г)![]() …
…
д)![]() е)
е) ![]() ..
..
3.2. Вкажіть правильну рівність:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
3.3. Виконавши наступні завдання, відгадай задумане слово:
-
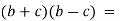 .. 2.
.. 2. 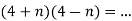
-
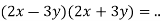 4.
4. 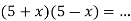
-
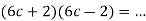 6.
6. 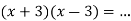
Таблиця-ключ
|
4x2-9y2 |
7a2+9b2 |
b2-c2 |
х2-9 |
4х2-9 |
36с2-4 |
49a2-81b2 |
8+n2 |
25-х2 |
2x2+3y2 |
16-n2 |
|
г |
м |
а |
д |
р |
б |
а |
н |
е |
о |
л |
- Виконайте вправу 505 (1,3 – на дошці; 2, 4 – самостійно) ст. 91.
- Виконайте вправу 513 (1, 3) ст. 91.
- Виконайте самостійно вправу 514 (1).
Урок №3
«Не на користь читать,
коли тільки вершки хапать»
Українське прислів’я
Фронтальне опрацювання матеріалу
Різниця квадратів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1- 1.2 блоку №5.
- Виконати інтелектуальну розминку, яка знаходиться за посиланням https://goo.gl/4WqfM9.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
-
Знайдіть значення виразу: 1)
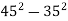 ; 2)
; 2) 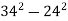 ; 3)
; 3) 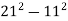 ; 4)
; 4) 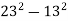 .
.
- Кожен варіант розв’язує своє завдання:
|
1 варіант |
2 варіант |
|
Розв’яжіть рівняння: |
Розв’яжіть рівняння: |
|
|
|
|
|
|
- Розбийтесь на пари і виконайте завдання:
|
І |
ІІ |
|
Розкладіть на множники: |
Розкладіть на множники: |
|
|
|
|
|
|
- Виправте помилки у розв’язуванні: Розкладіть на множники, користуючись формулою різниці квадратів:
-
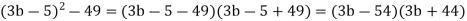 ;
;
-
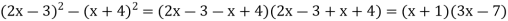
- Виконайте наступне завдання, зігравши у гру «Ланцюжок».
|
Розкладіть на множники вираз і запишіть отриманий результат в порожню клітинку таблиці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 3.
Спростити вираз, використовуючи формулу різниці квадратів (самостійно):
|
|
|
|
|
|
|
|
|
|
|
|
Уроки №4, 5
«...охота – мати праці, праця все перемагає»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Квадрат двочлена
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1, 2.3, 2.4 блоку № 5.
- Усно відповісти на питання:
- Чому дорівнює добуток різниці двох виразів та їх суми? Записати правило за допомогою формули.
- Чому дорівнює квадрат суми двох виразів? Записати правило за допомогою формули.
- Чому дорівнює квадрат різниці двох виразів? Записати правило за допомогою формули.
Завдання 2.
Усно виконати вправи:
- Квадрат суми двох виразів дорівнює:
|
А |
Б |
В |
Г |
|
квадрату цих виразів |
сумі квадратів цих виразів |
сумі квадратів цих виразів без їх подвоєного добутку |
квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу |
- Квадрат різниці двох виразів дорівнює:
|
А |
Б |
В |
Г |
|
різниці квадратів цих виразів |
квадрату першого виразу мінус подвоєний добуток цих виразів плюс квадрат другого виразу |
квадрату цих виразів |
квадрату першого виразу плюс подвоєний добуток цих виразів плюс квадрат другого виразу |
- Вправа 568, стор. 101 підручника.
Завдання 3.
Усно виконати вправи:
3.1. ![]() дорівнює многочлену:
дорівнює многочлену:
|
А |
Б |
В |
Г |
|
|
|
|
|
3.2. ![]() дорівнює многочлену:
дорівнює многочлену:
|
А |
Б |
В |
Г |
|
|
|
|
|
3.3. Якому з многочленів дорівнює ![]() :
:
|
А |
Б |
В |
Г |
|
|
|
|
|
3.4. Якому з многочленів дорівнює ![]() :
:
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання практичних умінь та навичок
Завдання 4.
![]() Замінити * одночленами так, щоб дістати тотожність
Замінити * одночленами так, щоб дістати тотожність
-

 (х2 + а)2 = + 2х2а + а2
(х2 + а)2 = + 2х2а + а2
-


 (6х – )2 = 36х2 – + 1
(6х – )2 = 36х2 – + 1
- ( – 4abс)2 = – 8abс +
Письмово виконати вправи з підручника, сторінки 101 – 102:
Завдання 5.
569 (1, 4, 8, 9, 11); 572 (2, 4, 6); 578 (3, 5); 580 (1, 4, 6).
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ
Завдання 6.
6.1. Встановіть відповідність:
І варіант
|
А) a2 – 2ab + b2 = |
|
Б) 4a2 +8ab + 4b2 = |
|
В) a2 + 4ab + 4b2 |
|
Г) 2a2 – 4ab + b2 = |
|
|
Д) 4a2 – 4ab + b2 = |
ІІ варіант
|
А) a2 + 2ab + b2 = |
|
Б) 4a2 – 8ab – 4b2 = |
|
В) a2 – 4ab + 4b2 = |
|
Г) 4a2 + 4ab + b2 = |
|
|
Д) 4a2 – 8ab + 4b2 = |
6.2. Вправа 594 з підручника, сторінка 104.
Завдання 7.
7.1. Замініть * одночленами так, щоб утворилась тотожність:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
7.2. Використовуючи формулу квадрата двочлена, обчисліть значення виразів: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Спростіть вираз: 1)
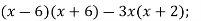 2)
2) 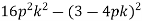 .
.
-
Користуючись формулою різниці квадратів двох виразів, обчисліть:
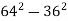 .
.
-
Спростіть вираз:
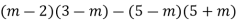 .
.
-
Спростіть вираз
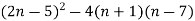 і знайдіть його значення, якщо
і знайдіть його значення, якщо 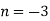 .
.
-
Розкладіть на множники вираз:
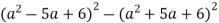 .
.
Урок №7
«Якщо ви досягли вершини - піднімайтесь вище»
Китайська мудрість
Фронтальне опрацювання матеріалу
Сума та різниця кубів двох виразів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези блоку № 5.
- Усно відповісти на питання:
- Чому дорівнює добуток різниці двох виразів та їх суми? Записати правило за допомогою формули.
- Чому дорівнює квадрат суми двох виразів? Записати правило за допомогою формули.
- Чому дорівнює квадрат різниці двох виразів? Записати правило за допомогою формули.
- Чому дорівнює сума кубів двох виразів? Записати правило за допомогою формули.
- Чому дорівнює різниця кубів двох виразів? Записати правило за допомогою формули.
Завдання 2.
Усно виконати вправи:
Віднови запис:
-
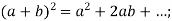
-
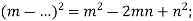
-
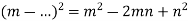 ;
;
-
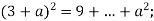
-

-
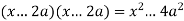 .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи, стор. 116 – 118 підручника: 678 (1, 3, 5, 7); 679; 685; 688, 690.
Урок №8
«Не кажи — не вмію, а кажи — навчусь!»
Українська мудрість
Фронтальне опрацювання матеріалу
Застосування різних способів розкладання многочлена на множники
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 5.
- Усно відповісти на питання:
- Чому дорівнює добуток різниці двох виразів та їх суми? Записати правило за допомогою формули.
- Чому дорівнює квадрат суми двох виразів? Записати правило за допомогою формули.
- Чому дорівнює квадрат різниці двох виразів? Записати правило за допомогою формули.
- Чому дорівнює сума кубів двох виразів? Записати правило за допомогою формули.
- Чому дорівнює різниця кубів двох виразів? Записати правило за допомогою формули.
- Чому дорівнює різниця квадратів двох виразів? Записати правило за допомогою формули.
- Які способи розкладання многочлена на множники ви знаєте?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Виконати усно вправи, запропоновані вчителем. (www.learningapps.org/1834002)
- Користуючись розглянутими прикладами, письмово виконайте вправи, стор. 122 підручника: 707 (1, 3, 5, 7, 9); 709 (2, 6); 711; 715.
Завдання 3.
- Розгляньте приклад 3, стор. 121 підручника.
- Користуючись розглянутим прикладом, письмово виконайте вправи, стор. 122 – 123 підручника: 717 (1, 3, 5, 7); 719 (2, 4, 6).
Урок №9
«Крапля довбає камінь не силою, а часто падаючи»
Джордано Бруно
Фронтальне опрацювання матеріалу
Застосування різних способів розкладання многочлена на множники
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези блоку № 5.
- Усно відповісти на питання:
- Чому дорівнює різниця квадратів двох виразів?
- Чому дорівнює різниця кубів двох виразів?
- Чому дорівнює сума кубів двох виразів?
- Чому дорівнює квадрат різниці двох виразів?
-
Чому дорівнює квадрат суми двох виразів?
- Записати в робочі зошити і дописати формули:
Завдання 2.
Усно виконати вправи:
-
Подай добуток
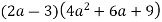 у вигляді многочлена.
у вигляді многочлена.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розклади двочлен
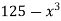 на множники.
на множники.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Відпрацювання практичних умінь та навичок
Письмово виконати вправи:
Завдання 3.
-
Розклади на множники: 1)
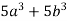 ; 2)
; 2) 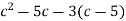 .
.
-
Розв’яжи рівняння:
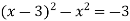 .
.
Завдання 4.
-
Розклади на множники:
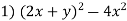 ; 2)
; 2) 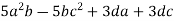 .
.
-
Доведи, що значення виразу
 ділиться на 10.
ділиться на 10.
Завдання 5.
Розклади на множники:
-
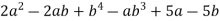 ;
;
-
 ;
;
-
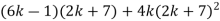 .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Розклади на множники: 1)
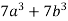 ; 2)
; 2) 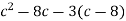 .
.
-
Розв’яжи рівняння:
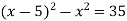 .
.
-
Розклади на множники:
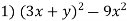 ; 2)
; 2) 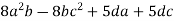 .
.
-
Доведи, що значення виразу
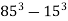 ділиться на 10.
ділиться на 10.
- Розклади на множники:
-
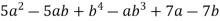 ;
;
-
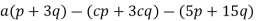 ;
;
-
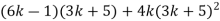 .
.
Урок №11
«Учись змолоду — пригодиться на старість»
Українське прислів’я
Внутрішньопредметне узагальнення матеріалу
Формули скороченого множення
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 5.
- Письмово відповісти на питання, запропоновані вчителем.
Завдання 2.
Усно виконати вправи:
2.1.Виконайте множення ![]() .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
2.2.Обчислити ![]() .
.
|
А |
Б |
В |
Г |
|
400 |
920 |
1600 |
1200 |
-
Подати тричлен
 у вигляді квадрата двочлена.
у вигляді квадрата двочлена.
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Узагальнення практичних умінь та навичок
Письмово виконати вправи:
Завдання 3.
- Обчисліть 68 · 72.
-
Розкласти на множники: а)
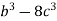 ; б)
; б) 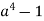 .
.
-
Подати у вигляді многочлена: а)
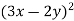 ; б)
; б) 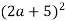 .
.
-
Розкласти на множники: а)
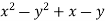 ; б)
; б) 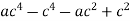 .
.
-
Розв’язати рівняння:
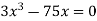 .
.
-
Доведіть, що вираз
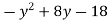 набуває лише від’ємних значень при будь-яких значеннях x.
набуває лише від’ємних значень при будь-яких значеннях x.
-
Доведіть, що вираз
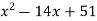 набуває лише додатних значень при будь-яких значеннях x.
набуває лише додатних значень при будь-яких значеннях x.
Домашнє завдання: для того, щоб краще підготуватись до контрольної роботи, виконайте інтерактивні завдання самостійно, або з однокласниками, яке знаходиться за посиланням http://LearningApps.org/view1961371
Повторення матеріалу, вивченого протягом року
Урок №1
«Добре того навчати, хто хоче все знати»
Українське прислів’я
Внутрішньопредметне узагальнення за рік
І. Узагальнення теоретичних знань
Завдання 1.
Дайте відповіді на питання:
- Що називають степенем з натуральним показником?
- Що називають одночленом?
- Дайте визначення многочлена.
- Які способи розкладання на множники многочленів вам відомі? В чому суть кожного з них?
- Що називають лінійним рівнянням з двома змінними?
- В чому суть методи підстановки і методу додавання розв’язування систем рівнянь?
- Сформулюйте формулу різниці квадратів, квадрата двочлена.
- Що означає розв’язати рівняння?
Завдання 2.
Усно виконати вправи:
-
Вкажіть, яке число є коренем рівняння
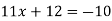 ?
?
|
А |
Б |
В |
Г |
|
2 |
– 2 |
8 |
– 8 |
-
Спростіть вираз
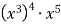 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яка пара чисел є розв’язком системи рівнянь
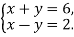
|
А |
Б |
В |
Г |
|
(5; 1) |
(2; 4) |
(3; 3) |
(4; 2) |
ІІ. Узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Розв’яжіть рівняння
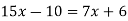 .
.
-
Спростіть вираз
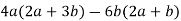 .
.
-
Розкладіть на множники: а)
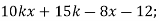 б)
б) 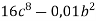 .
.
- Швидкість катера за течією річки дорівнює 16 км ∕ год, а проти течії – 8 км ∕ год. Знайдіть власну швидкість катера.
- В одному ящику було в 7 разів більше апельсинів, ніж у другому. Коли з першого ящика взяли 38 апельсинів, а з другого – 14, то в другому ящику залишилось на 78 апельсинів менше, ніж у першому. Скільки апельсинів було в кожному ящику спочатку?
1


про публікацію авторської розробки
Додати розробку