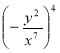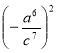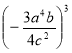Посібник для уроків алгебри І семестр 7 класу (оновлений)
Дана розробка може бути використана як додаток до уроків алгебри у І семестрі 7 класу, як роздатковий матеріал учням. Укладена згідно Комбінованої системи М.П. Гузика
Шановний семикласнику!
Ти починаєш вивчати новий шкільний предмет – алгебру.
Алгебра – це стародавня й мудра наука. Знайти її надзвичайно важливо. Алгебра – не тільки корисний, а й цікавий предмет, який розвиває кмітливість та логічне мислення. У цьому тобі допоможе навчальний посібник, який ти тримаєш в руках.
Посібник складається з трьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких ти зможеш засвоїти поняття, терміни і правила блоку навчальної інформації, також навчитись застосовувати ці знання для розв’язування різноманітних задач і вправ.
-
між уроками фронтального опрацювання ти будеш виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені
- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Нехай Бог посилає тобі мудрості у вивченні алгебри!!!
Тема №1. Функції
Урок №1

Функції
«…поняття функціональної залежності є
основне поняття всієї вищої математики…»
О. Я. Хінчин
Питання
- Функція.
- Лінійна функція.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §3, пункти 20 – 23, стор. 132 – 172.
|
1. Функція |
||
|
1.1 |
Якщо кожному значенню незалежної змінної ( |
Периметр квадрата – функція від довжини його сторони. Шлях – функція від часу. |
|
1.2 |
Усі значення, яких набуває незалежна змінна (х, абсциса, аргумент), утворюють область визначення функції. |
|
|
1.3 |
Усі значення, яких набуває залежна змінна (у, ордината, функція), утворюють область значень функції. |
|
|
1.4 |
Графіком функції називають фігуру, яка складається з усіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним значенням функції. |
|
|
1.5 |
Способи задання функції:
|
|
|
1.6 |
Якщо функція описує реальний процес, то кажуть, що вона є математичною моделлю даного процесу. |
Зміна температури, шлях, зміна площі і т. д. |
|
2. Лінійна функція |
||
|
2.7 |
Функцію, яку можна задати формулою виду |
|
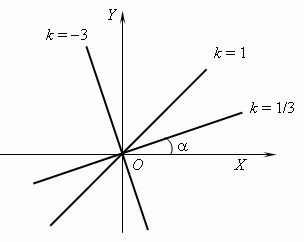
|
2.8 |
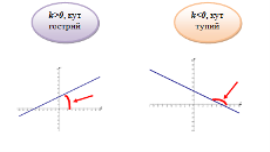
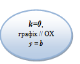
Від коефіцієнта k залежить кут, який утворює графік лінійної функції з додатним напрямком осі х, тому k називають кутовим коефіцієнтом прямої |
|
|
2.9 |
Властивості лінійної функції
|
|
|
2.10 |
Графіки функцій |
|
|
2.11 |
Функцію, яку задано формулою |
|
|
2.12 |
Графіком прямої пропорційності є пряма, яка проходить через початок координат. |
|
Урок №2
«Усе перевіряйте, чи воно
правильне, міцно тримайтесь того, що добре»
1 послання ап. Павла до солунян 5:21
Фронтальне опрацювання матеріалу
Функція. Область визначення і область значень функції. Способи задання функції. Графік функції
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 1.6 блоку навчальної інформації № 1.
- Усно дайте відповіді на запитання:
-
Що називають функцією
 від змінної
від змінної 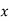 ?
?
- Що таке незалежна змінна?
- Що таке залежна змінна?
- Які є способи задання функції?
- Що таке область визначення і область значень функції?
- Що називають графіком функції?
- Що таке математична модель реального процесу?
Завдання 2.
- Переглянути відео «Функція у математиці», запропоноване вчителем.
- Усно розв’язати вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово розв’язати вправи, стор. 146 – 148 підручника: 792; 794; 805.
Завдання 4.
Письмово розв’язати вправи, стор. 156 – 157 підручника: 823; 832.
Урок №3
«Якщо людина живе тільки для себе,
єдине, чого вона заслуговує – презирства»
Цицерон
Фронтальне опрацювання матеріалу
Функція. Лінійна функція
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези блоку навчальної інформації № 1.
- Усно дайте відповіді на запитання:
- Що називають функцією?
- Що таке область визначення та область значень функції?
- Що називають графіком функції?
- Яка функція називається лінійною? Наведіть приклад.
- Що таке пряма пропорційність? Наведіть приклад.
- Що є графіком лінійної функції, прямої пропорційності?
- Вкажіть умови перетину та паралельності графіків лінійних функцій.
Завдання 2.
Усно виконати вправи:
- Нехай х см – довжина сторони рівностороннього трикутника, у – його периметр. Задайте формулою функцію у від х.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з наведених функцій не є лінійною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Функцію задано формулою
 . Яке значення функції відповідає значенню аргументу
. Яке значення функції відповідає значенню аргументу 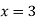 ?
?
|
А |
Б |
В |
Г |
|
6 |
2 |
8 |
4 |
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Функцію задано формулою
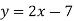 . Складіть таблицю значень функції, надавши аргументу значень – 4; – 1; 0; 2.
. Складіть таблицю значень функції, надавши аргументу значень – 4; – 1; 0; 2.
-
Функцію задано формулою
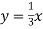 . При якому значенні аргументу значення функції дорівнює 12?
. При якому значенні аргументу значення функції дорівнює 12?
-
В одній системі координат побудувати графіки функцій
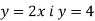 . Записати координати точки їх перетину.
. Записати координати точки їх перетину.
Завдання 4.
Письмово виконати вправи:
-
Функція задана формулою
 . Заповніть таблицю:
. Заповніть таблицю:
|
х |
|
– 15 |
|
1 |
|
– 1 |
|
у |
2 |
|
5 |
|
4 |
|
-
Побудувати графік функції
 . Користуючись графіком, знайти значення функції, якщо значення аргументу дорівнює 1.
. Користуючись графіком, знайти значення функції, якщо значення аргументу дорівнює 1.
-
Не виконуючи побудови, знайдіть координати точки перетину графіків функцій
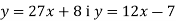 .
.
Домашнє завдання: встановити на смартфонах додаток «Графічний калькулятор. GeoGebra»
Урок №4
«Тисячі нерозгаданих таємниць таїть у собі наука,
і без вас, без вашої молодості, сміливості, ентузіазму,
вони не будуть розгадані. Наука чекає вас, друзі»
О.М. Несміянов, академік
Фронтальне опрацювання матеріалу
Лінійна функція
І. Робота над засвоєнням понять, термінів і правил

Завдання 1.
- Уважно прочитайте тези блоку навчальної інформації № 1.
- Усно дайте визначення поняттям, які є на хмарі слів:
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Письмово розв’язати вправи, стор. 164 підручника: 852, 858 (1), 869, 874 (1).
ІІІ. Відпрацювання практичних умінь та навичок розв’язування нестандартних задач і вправ
Завдання 3.
Виконайте практичну роботу в додатку «Графічний калькулятор GeoGebra». Для цього використайте інструкцію.
Інструкція до користування:
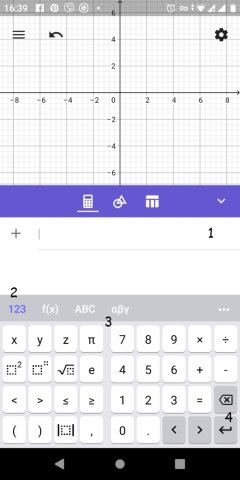
- Відкрийте додаток «Графічний калькулятор GeoGebra» на своїх смарфонах.
- У віконечку 1 введіть потрібну функцію, використовуючи панель вводу, перемикачі 2,3
- Натисніть на стрілочку 4, аби побудувати функцію.
Практична робота
|
Варіант 1 |
Варіант 2 |
|
1.Опівночі температура повітря була +3°С. До 8 години температура підвищувалась рівномірно на 1°С за кожну годину |
1.Опівночі температура повітря була -1°С. До 7 години температура знижувалась рівномірно на 2°С за кожну годину |
|
|
Пояснення:
Робота над самостійною підготує до сприйняття поняття лінійної функції.
|
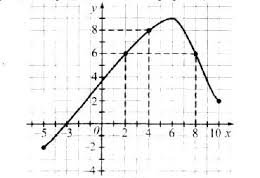
y – температура повітря, x – час. |
||
|
|
|
|
|
|
|
|
|
температура повітря: о 2 годині: 5°С о 6 годині: 9°С о 7 годині: 10°С |
температура повітря: о 2 годині: -5°С о 6 годині: -13 °С о 7 годині: -15°С |
|
Всі розв’язки запишіть у робочий зошит, а графік покажіть вчителю під час розв’язування.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Функцію задано формулою
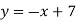 . Складіть таблицю значень функції, надавши аргументу значень – 4; – 3; – 2; 0; 1.
. Складіть таблицю значень функції, надавши аргументу значень – 4; – 3; – 2; 0; 1.
-
Функцію задано формулою
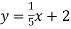 . При якому значенні аргументу значення функції дорівнює 7?
. При якому значенні аргументу значення функції дорівнює 7?
-
В одній системі координат побудувати графіки функцій
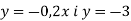 . Записати координати точки їх перетину.
. Записати координати точки їх перетину.
-
Функція задана формулою
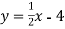 . Заповніть таблицю:
. Заповніть таблицю:
|
х |
– 8 |
|
– 2 |
|
6 |
|
|
у |
|
– 6 |
|
– 4 |
|
2 |
-
Побудувати графік функції
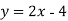 . Користуючись графіком, знайти значення аргументу, якщо значення функції дорівнює 4.
. Користуючись графіком, знайти значення аргументу, якщо значення функції дорівнює 4.
-
Не виконуючи побудови, знайдіть координати точки перетину графіків функцій
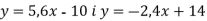 .
.
Завдання на вибір (виконані завдання здати на уроці індивідуального опрацювання):
- Підготувати 5 завдань «Функція. Лінійна функція».
- Скласти кросворд на 8 питань «Функція».
- Скласти розповідь «Наш туристичний похід» і намалювати графік руху туристів.
- Функція – це залежність. Складіть список речей, від яких залежить життя людини, доповніть його малюнками.
- Знайдіть кілька віршів з Біблії, де говориться, що ми залежимо від Бога.
Всі завдання повинні бути оформлені на стандартному листку А4, друковані, малюнки або намальовані від руки, або оформлені на комп’ютері у кольорі.
Урок №6
«Здобудеш освіту — побачиш більше світу»
Українське прислів’я
Внутрішньопредметне узагальнення матеріалу
Функція
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 1.
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Укажіть вираз, що задає функцію.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Лінійну функцію задано формулою
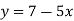 . Укажіть коефіцієнти
. Укажіть коефіцієнти 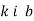 для цієї функції.
для цієї функції.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка з функцій є прямою пропорційністю?
|
А |
Б |
В |
Г |
|
|
|
|
|
ІІ. Узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
-
Функцію задано формулою
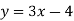 . Знайдіть:
. Знайдіть:
- значення функції, якщо значення аргументу дорівнює 4;
-
значення аргументу, при якому значення функції дорівнює
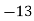 .
.
-
Функцію задано формулою
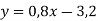 . Не виконуючи побудови, з’ясуйте чи проходить графік функції через точку
. Не виконуючи побудови, з’ясуйте чи проходить графік функції через точку 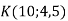 .
.
-
Побудуйте графік функції
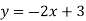 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
-
Функцію задано формулою
-
значення функції при
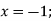
-
значення аргументу, при якому
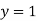 .
.
-
Побудуйте в одній системі координат графіки функцій:
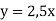 та
та 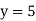 і знайдіть координати точки їх перетину.
і знайдіть координати точки їх перетину.
-
Знайдіть таке число b, щоб точка перетину графіків функцій
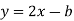 та
та  мала абсцису 2.
мала абсцису 2.
-
Побудуйте в одній системі координат графіки функцій:
Тема №2. Лінійні рівняння та їх системи
Урок №1

Лінійні рівняння та їх системи
«Алгебра – це, власне кажучи, аналіз рівнянь»
Жозеф Серре, французький математик
Питання
- Загальні відомості про рівняння.
- Лінійне рівняння з однією змінною.
- Лінійне рівняння з двома змінними.
- Системи двох лінійних рівнянь з двома змінними.
- Розв’язування задач за допомогою систем рівнянь.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §1, пункти 2 – 3, стор. 12 – 26; §4, пункти 24 – 29, стор. 173 – 218
|
1. Загальні відомості про рівняння |
||||||||||
|
1.1 |
Рівнянням називають рівність, що містить змінну. |
|
||||||||
|
1.2 |
Число, яке задовольняє рівняння, називають розв’язком або коренем рівняння. |
Число 2 є розв’язком рівняння |
||||||||
|
1.3 |
Розв’язати рівняння означає знайти його корені або довести, що їх немає. |
|||||||||
|
1.4 |
Два рівняння називаються рівносильними, якщо вони мають одні й ті ж самі корені. Рівносильними вважають і такі рівняння, які не мають коренів. |
|
||||||||
|
1.5 |
Властивості рівнянь:
|
|||||||||
|
2. Лінійне рівняння з однією змінною |
||||||||||
|
2.6 |
Рівняння виду |
|
||||||||
|
2.7 |
Числа |
|||||||||
|
2.8
|
Кількість коренів лінійного рівняння з однією змінною
|
|||||||||
|
3. Лінійне рівняння з двома змінними |
||||||||||
|
3.9 |
Лінійним рівнянням з двома змінними називають рівняння виду |
|
||||||||
|
3.10 |
Розв’язком рівняння з двома змінними називають пару значень змінних, для яких рівняння перетворюється у правильну рівність. |
1) (1; 2) 2) (3; 5) |
||||||||
|
3.11 |
Лінійні рівняння з двома змінними мають ті ж самі властивості, що і рівняння з однією змінною. |
|
||||||||
|
3.12 |
Графік рівняння з двома змінними утворюють усі точки координатної площини, координати яких є розв’язками даного рівняння. |
|||||||||
|
3.13 |
Графіком рівняння |
|||||||||
|
4. Системи двох лінійних рівнянь з двома змінними |
||||||||||
|
4.14 |
Якщо потрібно знайти спільні розв’язки двох рівнянь, то кажуть, що ці рівняння утворюють систему рівнянь. |
|
||||||||
|
4.15 |
Розв’язком системи двох рівнянь з двома змінними називають пару значень змінних, для яких кожне рівняння системи перетворюється у правильну числову рівність. |
(30; 26)
|
||||||||
|
4.16 |
Щоб розв’язати систему рівнянь графічним способом, потрібно побудувати графіки даних рівнянь в одній системі координат і знайти координати спільних точок цих графіків. |
|||||||||
|
4.17 |
Щоб розв’язати систему рівнянь способом підстановки, потрібно: 1) виразити з будь – якого рівняння системи одну змінну через іншу; 2) підставити в інше рівняння системи замість цієї змінної одержаний вираз; 3) розв’язати отримане рівняння з однією змінною; 4) знайти відповідне отриманому, значення першої змінної. |
Відповідь: (1; 2). |
||||||||
|
4.18 |
Щоб розв’язати систему рівнянь способом додавання потрібно: 1) помножити обидві частини рівнянь системи на такі числа, щоб коефіцієнти біля однієї зі змінних стали протилежними числами; 2) додати почленно ліві і праві частини рівнянь і замінити одне із рівнянь системи одержаним рівнянням; 3) розв’язати одержане рівняння з однією змінною; 4) знайти відповідне значення іншої змінної. |
Відповідь: (1; 2) |
||||||||
|
5. Розв’язування задач за допомогою систем рівнянь |
||||||||||
|
5.19 |
При розв’язуванні задач за допомогою систем рівнянь чинять так:
|
|||||||||
Урок №2
«Пам’ятайте, якщо ви бажаєте навчитися
плавати, то сміло заходьте у воду, а якщо бажаєте
навчитися розв’язувати задачі, то сміло розв’язуйте їх»
Дьордь Пойа, угорський, швейцарський, американський математик
Фронтальне опрацювання матеріалу
Загальні відомості про рівняння. Лінійне рівняння з однією змінною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 2.8 блоку № 2.
- Усно дайте відповіді на запитання:
- Що називають рівнянням?
- Що називається коренем рівняння?
- Що означає розв’язати рівняння?
- Сформулювати основні властивості рівнянь.
- Сформулювати означення лінійного рівняння з однією змінною.
Завдання 2.
Виконати усно:
- Назвати ліву і праву частину рівняння:
- 5x + 7 = 3x – 2;
- 0,5x = 4,7х + 8;
-
4у + 12 = 0.
- Пояснити, чому не має розв’язку рівняння:
- х + 3 = х;
-
5 – z = 8 – z.
- Розв’язати рівняння:
![]()
![]()
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
3.1. Письмово виконати вправи, стор. 14 – 17 підручника: 34 (1, 3, 5); 41; 45; 51 (1, 3, 5, 7, 9); 61 (1, 3).
3.2. Виконати самостійно завдання «Розшифруй слово», запропоноване вчителем.
Урок №3
«Неможливо правильно
керувати світом без Бога та Біблії»»
Джордж Вашингтон, 1-й президент США
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою лінійних рівнянь з однією змінною
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 2.8 блоку № 2.
- Усно дайте відповіді на запитання:
- Що називають рівнянням?
- Що називається коренем рівняння?
- Що означає розв’язати рівняння?
- Сформулювати основні властивості рівнянь.
- Сформулювати означення лінійного рівняння з однією змінною.
- Скільки розв’язків може мати лінійне рівняння і від чого це залежить?
Завдання 2.
- Прочитайте пункт 3, стор. 18 – 19 підручника.
- Усно дайте відповідь на питання:
- Що називають математичною моделлю реальної ситуації?
- За яким алгоритмом розв’язують задачі за допомогою лінійних рівнянь з однією змінною?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Назвіть невідомі величини
Позначте одну з них буквою;
Виразіть решту невідомих величин через ту, що позначили буквою
|
№ |
Фрагмент задачі |
Вираження невідомих |
|
1 |
У Василька і Марічки було грошей порівну |
Василько - |
|
Марічка - |
||
|
2 |
Один кілограм цукерок дорожчий за кілограм печива на 6 грн |
|
|
|
||
|
3 |
Пішохід прибув на 2 години пізніше, ніж велосипедист |
|
|
|
||
|
4 |
Один шматок дроту у 3 рази менший за другий |
|
|
|
||
|
5 |
Швидкість вантажівки на 48 км/год більша від швидкості легкової машини |
|
|
|
||
|
6 |
Віталій за день розв’язує 7 задач, а Мишко – 6. Скільки задач розв’яже кожен за х днів? |
|
|
|
Завдання 4.
Згадайте принци дії шалькових терез.
Допоможіть «відновити рівновагу» у наступних завданнях.
 Відповідь:
Відповідь:
Вираз А на 5 більший від виразу В А=3В
Вираз В у 5р більший від виразу А А=10В
Вираз А на 12 менший від виразу В А=В+12
Вираз В у 3р менший від виразу А А-5=В
Вираз А у 10р більший від виразу В 5А=В
Вираз В на 7 менший від виразу А А=В+7
Завдання 5.
В кошиках лежать свитки-задачі. Команди обирають задачу для колективного розв’язання. Необхідно за 15 хвилин розв’язати якомога більше задач. Можна розв’язувати по одній задачі всім разом, а можна й розподілити їх між членами команди.
На відкидних дошках необхідно записати рівняння, які склали в процесі розв’язання задач, та отримані відповіді.
- Задача з «Арифметики» Магницького (1703 р):
Послано одного гінця з Москви на Вологду, і велено йому в шляху своєму проходити щоденно по 40 верст. На другий день послано ще одного гінця слідом за першим і велено йому проходити по 45 верст щодня. Через скільки днів наздожене другий гонець першого?
(Нехай наздожене через х днів, тоді 40 х + 40 = 45 х;
Відповідь; через 8 днів)
- Задача з австралійського фольклору:
Батько запропонував своїм синам Альфреду, Джону та Чарльзу у спадок отару своїх овець розподілити так: Альфред одержить на 20% овець більше, ніж Джон і на 25% більше, ніж Чарльз. Джон одержить 3600 овець. Скільки овець одержить Чарльз ?
(Нехай Чарльз одержить х овець, Альфред - 3600+3660 • 0,2=4320 овець або х+0,25 х, тоді х + 0,25 х = 4320;
Відповідь: 3456 овець )
- Задача з «Курсу чистої математики» Войтяховського (1811 р):*
За легендою, одна чеська панянка вирішила вийти заміж за того, хто розв’яже задачу: «Скільки слив було в кошику, з якого вона дала першому нареченому половину всіх слив та ще одну, другому – половину залишку та ще одну, третьому – половину нового залишку і ще 3 сливи, після чого в кошику не залишилося нічого?»
- Для нового кабінету гімназії потрібно придбати комплект меблів: 15 парт та 30 стільців. Завгосп просить нас вказати ціну парти та стільця, якщо директор повідомила її, що загальна сума витрат складає 14 100 грн, а парта дорожча за стілець на 280 грн.
- У комірчині стояло 2 мішки зі стартовою та фінішною шпаклівкою по 30 кг в кожному. Для ремонту з першого мішка взяли втричі більше шпаклівки, ніж з другого, після чого в ньому стало в 2 рази менше шпаклівки. Скільки залишилось матеріалу в кожному мішку?
Урок №4
«Я все можу в Тім, Хто мене підкріпляє,
в Ісусі Христі»
До филип’ян 4:13
Фронтальне опрацювання матеріалу
Лінійне рівняння з двома змінними та його графік
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 3.12 блоку №2.
- Прослухайте казку «Дід Рівняло».
- Усно дайте відповідь на питання:
- Що називається розв’язком рівняння з двома змінними?
-
Чи є пара чисел (4;1) розв’язком рівняння
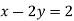 ?
?
- Що називається графіком рівняння з двома змінними? Чи завжди таке рівняння має графік?
- Які рівняння називаються рівносильними? Яку властивість мають графіки рівносильних рівнянь?
- Серед даних рівнянь із двома змінними виберіть пари таких, що мають однакові графіки та поясніть, чому ви так вважаєте:
-
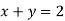 ; 2)
; 2) 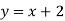 ; 3)
; 3) 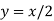 ; 4)
; 4)  ; 5)
; 5) 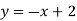 .
.
- Виконайте усно вправи:
Серед поданих рівнянь назвіть лінійні рівняння з двома невідомими:
-
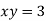 ; 2)
; 2) 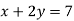 ; 3)
; 3) 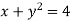 ; 4)
; 4) 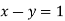 ; 5)
; 5) 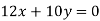 ;
;
![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() 9)
9) ![]() .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Виконайте письмово вправи:
-
Які з пар чисел (2;2); (1;3); (1;3,5);
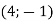 є розв’язками рівняння
є розв’язками рівняння 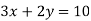 ?
?
-
Виразіть
 через
через 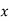 у рівняннях та знайдіть два які-небудь розв’язки рівнянь:
у рівняннях та знайдіть два які-небудь розв’язки рівнянь:
-
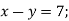 2)
2) 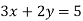 .
.
-
Які з точок
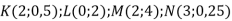 не належать графіку рівняння
не належать графіку рівняння 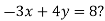
- Побудуйте графік рівняння:
-
Які з точок
![]() .
.
-
На прямій, яка є графіком рівняння
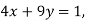 узяли точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.
узяли точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.
-
Знайдіть значення коефіцієнта
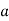 в рівнянні
в рівнянні 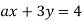 , якщо відомо, що графік рівняння проходить через точку (1;2).
, якщо відомо, що графік рівняння проходить через точку (1;2).
Урок №5
«А якщо кому з вас не стачає мудрості,нехай просить
від Бога, що всім дає просто, та не докоряє, – і буде вона йому дана»
Якова 1:5
Фронтальне опрацювання матеріалу
Системи лінійних рівнянь. Графічний спосіб розв’язування систем
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Уважно прочитайте тези 1.1 – 4.16 блоку № 2.
- Усно дайте відповідь на питання:
- У якому випадку говорять, що треба розв’язати систему рівнянь?
- Що є розв’язком системи рівнянь з двома змінними?
- Що означає розв’язати систему рівнянь?
- У чому суть графічного методу розв’язування систем рівнянь з двома змінними?
- Що називають лінійним рівнянням з двома змінними?
- Які властивості рівнянь вам відомі?
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
Усно виконайте вправу 1007, стор. 194 підручника.
Завдання 3.
Письмово виконайте вправи, стор. 194 – 195 підручника: 1009 (2), 1010 (1, 5).
Завдання 4.
Письмово виконайте вправи:
-
На графіку рівняння
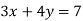 взято точку з абсцисою 1. Знайти ординату цієї точки.
взято точку з абсцисою 1. Знайти ординату цієї точки.
-
Знайдіть усі пари натуральних чисел, які є розв’язками рівняння
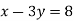 .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
 Розв’яжіть рівняння
Розв’яжіть рівняння 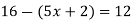 .
.
- У першій пачці в 5 раз більше зошитів, ніж у другій. Коли з першої пачки переклали у другу 12 зошитів, то в обох пачках зошитів стало порівну. Скільки їх було у кожній пачці спочатку?
-
Розв’яжіть графічно систему рівнянь
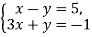
-
На графіку рівняння
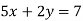 взято точку з абсцисою 3. Знайдіть ординату цієї точки.
взято точку з абсцисою 3. Знайдіть ординату цієї точки.
-
Знайдіть усі пари натуральних чисел, які є розв’язками рівняння
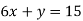 .
.
Уроки №7, 8
"Ні про що не турбуйтесь, а в усьому нехай
виявляються Богові ваші бажання молитвою
й проханням з подякою"
Филип'ян 4:6
Фронтальне опрацювання матеріалу
Розв’язування систем лінійних рівнянь способом підстановки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 4.14 – 4.17 блоку № 2.
- Усно дайте відповіді на запитання:
- Коли кажуть, що рівняння утворюють систему рівнянь?
- Що називають розв’язком системи лінійних рівнянь?
- Сформулюйте алгоритм розв’язування систем рівнянь способом підстановки.
- Як ви вважаєте, коли найкраще використовувати метод підстановки при розв’язуванні рівнянь?
Завдання 2.
Виконайте усно вправи
-
Чи є розв’язком системи
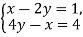 пара чисел:
пара чисел:
-
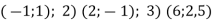 ?
?
-
Виразіть
 через
через 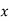 з рівняння:
з рівняння:
-
Виразіть
-
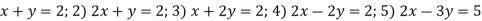 .
.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконайте вправи:
-
Використовуючи алгоритми та приклади, розв’яжіть систему способом підстановки:
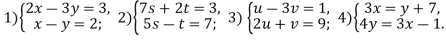
- Знайдіть координати точок перетину графіків рівнянь, не виконуючи побудов:
-
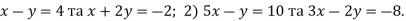
-
Знайдіть розв’язки системи рівнянь
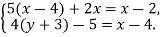
- Знайдіть помилку в розв’язанні:
-
Знайдіть розв’язки системи рівнянь
![]()
Відповідь: (3;2).
Завдання 4.
Заповніть пропуски так, щоб утворені записи були правильні (розв’язання системи способом підстановки):
![]()
Завдання 5.
Розв’яжіть методом підстановки
a)![]() б)
б)![]() в)
в)![]()
Завдання 6.
 Практична робота.
Практична робота.
Тема. Розв’язування систем лінійних рівнянь з двома змінними способом підстановки
Мета: формування вмінь розв’язувати системи лінійних рівнянь з двома змінними способом підстановки.
Завдання. Розв’язати систему лінійних рівнянь з двома змінними способом підстановки: ![]()
Хід роботи:
- Вирази з другого рівняння системи змінну х через змінну у.
- Підстав в перше рівняння системи замість змінної х здобутий вираз.
- Розв’яжи отримане рівняння з однією змінною.
- Знайди відповідне значення другої змінної.
- Переконайся, що отримані значення є коренями кожного з рівнянь.
- Зроби висновок щодо отриманих значень.
-
 Запиши відповідь.
Запиши відповідь.
Уроки №9, 10
«З ким поведешся, від того і наберешся»
Українське прислів’я
Фронтальне опрацювання матеріалу
Розв’язування систем лінійних рівнянь способом додавання
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези 1.1 – 4.17 блоку №2.
- Усно дайте відповіді на питання:
- Скількома способами можна розв’язувати системи лінійних рівнянь з двома змінними?
- Що називають рівнянням?
- Що означає розв’язати рівняння?
- В чому суть методу підстановки розв’язування систем рівнянь?
- Коли виникає необхідність розв’язати систему рівнянь?
- Що називають розв’язком системи рівнянь з двома змінними?
- В чому суть методу додавання?
Завдання 2.
Виконайте усні вправи, запропоновані вчителем у презентації.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
3.1. Виконайте письмово вправи зі ст. 202 – 205:
1047 (1, 3, 5), 1050 (2, 6), 1053 (1).
3.2. Виконайте угорський кросворд «Рівняння:
Ось зараз і ви побуваєте у ролі дешифрувальника. Вам потрібно спочатку записати у зошитах назви понять, про які йдеться.
1. Значення змінної, при якому рівняння стає правильною рівністю. (Корінь).
2. Розв’язком рівняння з двома змінними є… (пара) чисел.
3. Як називається рівняння виду ах+ву=с ? (Лінійне).
4. Якого математика називають батьком алгебри, а також він ввів позначення коефіцієнтів буквами? (Вієт).
5. Яка наука розвивалась багато століть як наука про рівняння? (Алгебра).
6. Змінна у рівнянні. (Невідоме).
7. Рівність, яка містить невідоме. (Рівняння).
Учні одержують таблиці по варіантах.
Знайти записані відповіді на таблицях, викреслити їх. Прочитати утворені слова. Таблиця 1.
|
І |
Н |
Ь |
Ш |
Л |
|
Р |
Р |
І |
В |
І |
|
О |
М |
І |
Н |
Н |
|
К |
Д |
Я |
Я |
і |
|
П |
Т |
Н |
Н |
Й |
|
А |
Р |
А |
Е |
Н |
Закреслені слова: корінь, пара, лінійне, рівняння. Відповідь. Шмідт. Таблиця 2.
|
Е |
В |
І |
Д |
О |
|
Н |
В |
В |
І |
М |
|
К |
О |
І |
Є |
Е |
|
Н |
Р |
І |
Т |
А |
|
И |
І |
Н |
Ь |
Л |
|
А |
Р |
Б |
Е |
Г |
Закреслені слова: невідоме, Вієт, алгебра, корінь.
Завдання 4.
Розв’язати системи рівнянь способом додавання:
а)  б)
б) 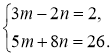
Завдання 5.
 Практична робота.
Практична робота.
Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання
Мета: формування вмінь розв’язувати системи лінійних рівнянь з двома змінними способом додавання.
 Завдання. Розв’язати систему лінійних рівнянь з двома змінними способом додавання:
Завдання. Розв’язати систему лінійних рівнянь з двома змінними способом додавання:
Хід роботи:
- Помнож перше рівняння на 2, щоб коефіцієнти при змінній у стали протилежними числами.
- Додай почленно ліві і праві частини рівнянь системи.
- Розв’яжи утворене рівняння з однією змінною х.
- Підстав знайдене значення х в перше початкове рівняння і знайди відповідне значення у.
- Переконайся, що отримані значення є коренями кожного з рівнянь.
- Зроби висновок щодо отриманих значень.
- Запиши відповідь.

Урок №11
«Діяльність - єдиний шлях до знання»
Б. Шоу
Фронтальне опрацювання матеріалу
Розв’язування задач за допомогою систем рівнянь
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторіть тези блоку №2.
- Завершіть речення:
- Рівність, яка містить невідоме, називається …
- Значення змінних, для яких рівняння перетворюється у правильну числову рівність, називається …
- Розв’язати рівняння означає …
- Якщо потрібно знайти спільні розв’язки двох чи кількох рівнянь, говорять, що ці рівняння утворюють …
- Математичною моделлю задачі є …
-
Як розв’язувати задачі за допомогою систем рівнянь?
- Що зайве? Чому?
а) «система, графік, змінна, розв’язок, спілкування»;
б) «рівність, рівняння, речення, тотожність»;
в) «число, значення, лікування, формула, задача»
Завдання 2.
Розгляньте приклад розв’язування задачі:
Учень задумав два числа, сума яких дорівнює 100, а різниця – 26. Які числа задумав учень?
Нехай х – перше число, тоді у – друге число. Оскільки їх сума дорівнює 100, то маємо рівняння: х + у = 100.
За другою умовою задачі маємо рівняння: х – у = 26.
Складемо систему рівнянь:
![]() та розв’яжемо способом додавання
та розв’яжемо способом додавання
2х = 126
х = 63
у = 37
Відповідь: перше число 63, друге – 37.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконайте вправи:
- За 7 кг апельсинів і 4 кг лимонів заплатили 26 грн. Скільки коштує 1 кг апельсинів і скільки 1 кг лимонів, якщо 5 кг апельсинів дорожчі за 2 кг лимонів на 4 грн?
- 20% від одного числа і 60% від другого числа разом дорівнюють 37. Знайдіть ці числа, якщо їх сума дорівнює 25.
- Теплохід проходить за 2 год за течією річки й за 3 год проти течії 222 км. За 3 год за течією річки він проходить на 60 км більше, ніж за 2 год проти течії. Знайдіть швидкість теплохода в стоячій воді та швидкість течії річки.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
У порожні клітинки впишіть слова, пов'язані з математикою, так, щоб збігались перша й остання букви та кількість букв у слові.
|
ч |
|
|
|
|
|
|
|
к |
|
Д |
|
|
|
|
|
|
ь |
|
|
к |
|
|
|
|
|
т |
||
|
ч |
|
|
|
|
и |
|
|
|
|
ч |
|
|
|
0 |
|
|
||
|
д |
|
|
б |
|
|
|
||
|
к |
|
т |
|
|
|
|||
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Розв
 язати систему рівнянь способом додавання
язати систему рівнянь способом додавання 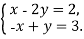
-
Розв
 язати систему рівнянь способом підстановки
язати систему рівнянь способом підстановки 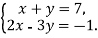
-
Розвяжіть систему рівнянь
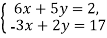 .
.
- 70% від одного числа на 20 більше за 60% від другого числа. Знайдіть ці числа, якщо їх сума дорівнює 75.
Урок №13
«Любов виникає з любові; коли хочу,
щоб мене любили, я сам перший люблю»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Лінійні рівняння та їх системи
І. Узагальнення теоретичних знань
Завдання 1.
- Повторити блок № 2.
- Письмово відповісти на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконати вправи:
- Яке з рівнянь є лінійним рівнянням?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Вкажіть розв’язок рівняння
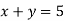 .
.
|
А |
Б |
В |
Г |
|
(– 5; 1) |
(5; 0) |
(– 5; 6) |
(– 4; 4) |
-
Запишіть пару чисел, яка є розв’язком системи
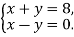
|
А |
Б |
В |
Г |
|
(6; 2) |
(4; 4) |
(5; 3) |
(8; 0) |
Завдання 3.
Письмово виконати вправи:
-
Розв’яжіть рівняння:
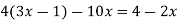 .
.
-
Розв’яжіть систему рівнянь способом підстановки
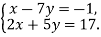
-
Розв’яжіть систему рівнянь
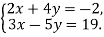
- Розв’яжіть задачу за допомогою рівняння:
На одному складі було в 3 рази більше телевізорів, ніж на другому. Після того, як з першого складу взяли 20 телевізорів, а на другий привезли 14, телевізорів на обох складах стало порівну. Скільки телевізорів було на кожному складі спочатку?
- Розв’яжіть систему рівнянь:
![]()
Тема №3. Цілі вирази. Степінь з натуральним показником. Одночлен
Урок №1

Цілі вирази. Степінь з натуральним показником. Одночлен
«Ледача рука до убозтва
веде, рука ж роботяща збагачує»
Книга приповістей Соломонових 10:4
Питання
- Вирази зі змінними. Цілі вирази.
- Тотожно рівні вирази. Тотожності.
- Степінь з натуральним показником.
- Властивості степеня з натуральним показником.
- Одночлен та його стандартний вигляд.
Література
Мерзляк А., Полонський В., Якір М. Алгебра: Підручник для 7 класу, Харків, «Гімназія», 2015, §2, пункти 4 – 7, стор. 27 - 53.
|
||
|
1.1 |
Виразом зі змінними називають вираз, утворений зі змінних, чисел, знаків дій і дужок. |
|
|
1.2 |
Значенням числового виразу, який одержимо, підставивши у вираз зі змінними замість змінних їхні значення, називають значенням виразу зі змінними |
Якщо
|
|
1.3 |
Вирази, які не містять дії ділення на вираз зі змінними, називають цілими. |
|
|
1.4 |
Вирази, які містять дію ділення на вираз зі змінними, називають дробовими. |
|
|
1.5 |
Вирази зі змінними використовують для запису формул |
|
|
||
|
2.6 |
Вирази, відповідні значення яких є рівними при будь-яких значеннях змінних, що входять до них, називають тотожно рівними. |
|
|
2.7 |
Рівність, яка є правильною для всіх значень змінних, називають тотожністю. |
|
|
2.8 |
Заміну одного виразу тотожно рівним йому виразом називають тотожним перетворенням виразу
|
|
|
2.9 |
При доведенні тотожностей використовують такі способи:
|
|
|
||
|
3.10 |
Степенем числа а з натуральним показником n, більшим за 1, називають добуток n множників, кожен з яких дорівнює a |
n разів
|
|
3.11 |
Степенем числа а з показником 1 називають саме число а. |
|
|
3.12 |
Степінь від’ємного числа з парним показником є число додатне. Степінь від’ємного числа з непарним показником є число від’ємне. |
|
|
3.13 |
Будь-який натуральний степінь числа 0 дорівнює 0. |
|
|
||
|
4.14 |
Щоб перемножити степені з однаковими основами, потрібно основу залишити ту саму, а показники степенів додати: |
|
|
4.15 |
Щоб поділити степені з однаковими основами, потрібно основу залишити ту саму, а від показника степеня діленого відняти показник степеня дільника: |
|
|
4.16 |
Щоб піднести степінь до степеня, потрібно основу залишити ту саму, а показники степенів перемножити: |
|
|
4.17 |
Щоб піднести до степеня добуток, досить піднести до цього степеня кожний множник і результати перемножити: |
|
|
||
|
5.18 |
Одночленом називають добуток чисел, змінних, та їхніх степенів. Змінні, числа та їхні степені також вважаються одночленами. |
|
|
5.19 |
Одночлен, записаний у вигляді добутку числового множника, який стоїть на першому місці, і степенів різних змінних, називають одночленом стандартного вигляду. |
|
|
5.20 |
Числовий множник одночлена, записаного у стандартному вигляді, називають коефіцієнтом одночлена. |
|
|
5.21 |
Степенем одночлена називають суму показників степенів усіх змінних, які входять до нього. Якщо одночленом є число, то вважають, що степінь такого одночлена дорівнює 0. |
|
Урок №2
«І все, що тільки чините,
робіть від душі, як Господу, а не людям»
Послання св. апостола Павла до Колосян 3 : 23
Фронтальне опрацювання матеріалу
Вирази зі змінними
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 1.1 – 1.5 блоку № 3.
- Усно дати відповідь на питання:
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Дайте визначення цілого виразу. Наведіть приклади.
- Що називають дробовим виразом? Наведіть приклади дробових виразів.
- Де використовують вирази зі змінними?
Завдання 2.
Прочитайте вираз, використовуючи терміни «сума», «різниця», «квадрат», «куб» тощо.
-
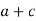 ;
;
-
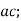
-
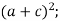
-
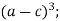
-
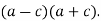
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконати вправи:
3.1. Заповніть таблицю, обчисливши значення виразу ![]() для заданих значень
для заданих значень ![]() :
:
|
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
3.2. Запишіть у вигляді виразу:
1) різницю чисел ![]() і
і ![]() ;
;
2) квадрат суми чисел ![]() і
і ![]() ;
;
3) суму куба числа ![]() і квадрата числа
і квадрата числа ![]() ;
;
4) квадрат різниці чисел ![]() і
і ![]() ;
;
5) різницю квадратів чисел ![]() і
і ![]() ;
;
6) півсуму добутку чисел 0,7 і ![]() та числа –0,6.
та числа –0,6.
3.3. Відомо, що ![]() Знайдіть значення виразу:
Знайдіть значення виразу:
-
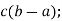
-
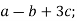
-
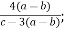
-
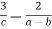 .
.
3.4. Складіть вираз для розв’язування задачі:
- Периметр прямокутника 16 см, одна з його сторін m см. Яка площа прямокутника?
-
З двох міст, відстань між якими S км, назустріч одне одному виїхали два автомобілі. Швидкість одного з них
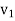 км/год, а швидкість другого –
км/год, а швидкість другого – 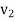 км/год. Через скільки годин вони зустрінуться?
км/год. Через скільки годин вони зустрінуться?
Урок №3
«Світ математики – це немовби багатоповерхова
будівля, причому ідеї кожного поверху зв’язані як між
собою, так і з тими, що знаходяться вище і нижче»
Годфрі Харолд Харді, англійський математик
Фронтальне опрацювання матеріалу
Тотожно рівні вирази. Тотожності
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.9 блоку № 3.
- Усно дай відповідь на питання:
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Які вирази називаються тотожно рівними?
- Що називають тотожністю?
- Записані нижче рівності є тотожностями. Заповніть пропуски:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
- Якщо один із виразів замінити тотожно рівним йому виразом, то така заміна називається... перетворенням.
- Які прийоми використовують при доведенні тотожностей?
-
Із запропонованих слів (словосполучень) утворіть пари, об’єднані певною (однією) логікою (змістом): 1) вирази; 2) тотожність; 3) заміна; 4) тотожно рівні; 5) рівність; 6) тотожне перетворення. Поясніть логіку.
- Відгадайте ребуси, запропоновані вчителем.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 2.
- Розглянь приклад 1 на стор. 29 підручника.
- Користуючись розглянутим прикладом, письмово виконай вправи, стор. 30 – 31 підручника: 134, 138 (1, 3, 5), 141, 142 (2, 3).
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Спростіть вираз:
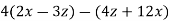 .
.
-
Доведіть тотожність:
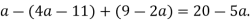
-
Спростити вираз і знайти його значення:
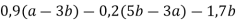 , якщо а = 2, b = 3.
, якщо а = 2, b = 3.
-
Доведіть тотожність
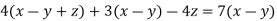 .
.
-
Доведіть тотожність:
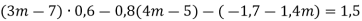 .
.
Урок №5
«Без бажання все важке, навіть найлегше»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Степінь з натуральним показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.10 – 3.13 блоку № 3.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
Завдання 2.
Уважно прочитайте повідомлення
Слово Exponent, яке ввів для показника степеня Штифель в 1553 році, означає «показник», » позивач». Показники степеня в сьогоднішньому вигляді ввів до науки Декарт (1637). Англієць за народженням, що жив у Франції, Юг писав 5аIV , Ерігон – 5а4, у Декарта ці символи перетворились в 5а4. Вираз «піднесення до степеня» вперше з’явився в 1716 році в роботі »Mathematische Lexicon» Вольфа.
Дайте відповіді на питання:
- Хто вперше ввів поняття степеня?
- Хто запропонував поняття «піднесення до степеня»?
- Кому ми завдячуємо сучасним виглядом показника степеня?
Завдання 3.
3.1. Перегляньте відео «Що таке степінь?»
3.2. Усно виконати вправу (стор. 34): 152.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 4.
Письмово виконати вправи (стор.36 – 38): 162, 165 (1, 3), 166 (2, 4, 6), 175, 177, 185.
Уроки № 6 – 8
«Не все те отрута, що неприємне на смак»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Властивості степеня з натуральним показником
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити тези 3.10 – 4.17 блоку № 3.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
- Як перемножити степені з однаковими основами?
- Як поділити степені з однаковими основами?
- Як піднести степінь до степеня?
- Як піднести до степеня добуток?
Завдання 2.
Усно виконати вправи (стор. 43): 205, 206, 208, 211.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
 Користуючись різними властивостями степеня з натуральним показником, на пелюстках ромашки напишіть вирази, які б дорівнювали виразу усередині:
Користуючись різними властивостями степеня з натуральним показником, на пелюстках ромашки напишіть вирази, які б дорівнювали виразу усередині:
Письмово виконати вправи (стор. 43 – 45 ):
Завдання 4.
215, 220, 221 (1, 3, 5, 7), 224, 231.
Завдання 5.
|
1. Запишіть у вигляді степеня: |
||
|
1)
2) |
3) |
4) |
|
2. Спростіть вираз: |
||
|
1)
2) |
3) |
4) |
|
3. Знайдіть значення виразу: |
||
|
1)
2) |
3) |
4) |
|
4. Замініть зірочку степенем так, щоб утворилась правильна рівність: |
||
|
- |
а4 ∙ * : а13 = а2 |
- |
|
5. Піднесіть до степеня дріб: |
||
|
1)
2) |
3) |
4) |
|
6. Порівняйте: |
||
|
1) 85 та 214; 2) 1253 та 255;
|
3) 93 та 272 |
4)
|
Завдання 6.
Виконайте вправи 236, 242 на ст. 45 вашого підручника.
Завдання 7.
-
Спростіть:
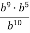 .
.
-
Обчислити, використовуючи властивості степеня:
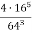 .
.
-
Знайдіть значення виразу:
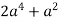 при
при 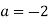 .
.
-
Спростити вираз: а)
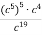 ; б)
; б) 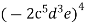 .
.
-
Обчислити, використовуючи властивості степеня:
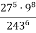 .
.
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Виконайте дії: а)
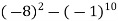 ; б)
; б) 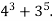
-
Спростіть:
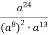 .
.
-
Обчислити, використовуючи властивості степеня:
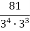 .
.
-
Знайдіть значення виразу:
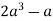 при
при 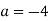 .
.
-
Спростити вираз: а)
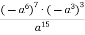 ; б)
; б)  .
.
-
Обчислити, використовуючи властивості степеня:
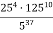 .
.
Урок № 10, 11
«Визначай смак не по шкаралупі, а по ядру»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Одночлен. Стандартний вигляд одночлена
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повторити блок № 3.
- Усно дати відповідь на питання:
- Що називається степенем числа а з натуральним показником n?
- Що називають степенем числа а з показником 1?
- Чому дорівнює степінь від’ємного числа з парним і непарним показником степеня?
- Чому дорівнює будь-який натуральний степінь числа 0?
- Як перемножити степені з однаковими основами?
- Як поділити степені з однаковими основами?
- Як піднести степінь до степеня?
- Як піднести до степеня добуток?
- Що називається одночленом?
- Що таке стандартний вигляд одночлена?
- Що називають степенем одночлена?
- Що називають виразом зі змінними?
- Що називають значенням виразу зі змінними?
- Які вирази називаються тотожно рівними?
- Що називають тотожністю?
- Які прийоми використовують для доведення тотожностей?
Завдання 2.
Усно виконати вправи з підручника (стор. 50): 261, 262, 263.
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
3.1. Письмово виконати вправи з підручника (стор. 50 – 52): 266, 274, 276 (1, 3), 280 (1, 2, 6).
3.2. Відгадайте зашифроване слово

Код
|
х8 |
х9 |
8х9 |
90х8 |
х8 |
90х8 |
|
|
|
|
|
|
|
Виконати завдання: https://learningapps.org/6356889: Вкажіть одночлени стандартного вигляду.
Завдання 4.
Письмово виконати вправи:
-
Звести одночлен до стандартного вигляду, вказати його коефіцієнт і степінь: 1)
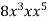 ; 2)
; 2) 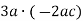 ; 3)
; 3) 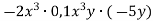 .
.
-
Знайдіть значення одночлена: 1)
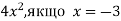 ;
;
2) ![]()
![]() ,
, ![]() ;
;
3) ![]() , якщо
, якщо ![]()
Завдання 5.
Письмово виконати вправи:
-
Знайдіть значення виразу:
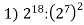 ; 2)
; 2) 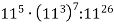 ; 3)
; 3) 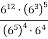 .
.
-
Знайдіть значення виразу: 1)
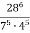 ; 2)
; 2) 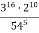 ; 3)
; 3) 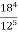 .
.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 6. (домашнє)
Якщо ти бажаєш отримати додатковий бал на індивідуальному опрацюванні матеріалу, виконай кросворд, який знаходиться за посиланням http://LearningApps.org/watch?v=p07yn31va01
Коли виконаєш його, зроби скрін екрану і покази вчителеві.
Гра «Кросворд» (Мета гри відгадування кросворду із ключовим словом)
- Рівність, що правильна при будь-яких значеннях змінних(тотожність)
- Добуток кількох множників рівних між собою(степінь)
- Раціональний вираз, який не містить ділення на вираз із змінною (цілий)
- Вираз, що складається з добутка числа, однієї або декількох букв (змінних) та їх степенів з натуральним показником (одночлен)
- Числовий множник одночлена, записаного в стандартному вигляді (коефіцієнт)
- Добуток двох однакових множників (квадрат)
- Добуток трьох однакових множників (куб)
- Парний степінь від’ємного числа є числом (додатним)
- Непарний степінь від’ємного числа є числом (від’ємним)
- Вираз, до складу якого входять числа, знаки дій і дужки (числовий)
- Значення змінних, для яких можна знайти відповідне значення виразу(допустимі)
- Вираз, складений із чисел, змінних за допомогою дій додавання, віднімання, множення, ділення й піднесення до степеня та дужок, що визначають порядок дій (раціональний)
- Розділ математики, що вивчається у 7-11 класах (алгебра)
Ключове слово Остоградський
Остроградський Михайло Васильович - видатний математик ХІХст. Народився в Україні на Полтавщині. За свої видатні заслуги був обраний дійсним членом Петербурзької, Американської, Туринської академії наук, членом кореспондентом Паризької академії наук. Прославився тим, що вніс суттєві доповнення до математичного аналізу, алгебри і теорії чисел.
![]()
Готуємось до індивідуального опрацювання матеріалу
-
Обчисли значення одночлена
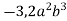 при
при 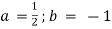 .
.
-
Спрости вираз: 1)
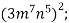 2)
2) 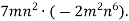
-
Запиши одночлен
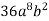 у вигляді квадрата одночлена.
у вигляді квадрата одночлена.
-
Спрости вираз: 1)
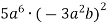 ; 2)
; 2) 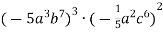 .
.
-
Подай вираз у вигляді куба одночлена
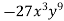 .
.
-
Спрости вираз:
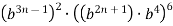 .
.
- Піднести одночлен до степеня: https://learningapps.org/3757013
Урок № 13
«...найкраща помилка та, яку допускають при навчанні»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Цілі вирази. Степінь з натуральним показником. Одночлен
І. Засвоєння термінології до теми
Завдання 1.
- Повтори блок № 3, особливу увагу зверни на тези 1.1, 1.2, 3.10, 3.12, 4.14 – 5.19, 5.21.
- Письмово дай відповіді на питання, запропоновані вчителем.
ІІ. Узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Запиши у вигляді степеня з основою
 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Вкажи, який з поданих виразів не є цілим:
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисли значення виразу
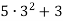 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
Завдання 3.
Письмово виконай вправи:
-
Подай у стандартному вигляді одночлен:
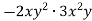 .
.
-
Виконай дії:
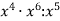 .
.
-
Спрости вираз:
 .
.
-
Доведи тотожність:
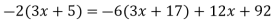 .
.
-
На першій полиці стоїть
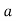 книжок, на другій – утричі більше, ніж на першій, а на третій – на 17 книжок менше, ніж на першій і на другій полицях разом. Запиши у вигляді виразу кількість книжок на трьох полицях разом. Обчисли при
книжок, на другій – утричі більше, ніж на першій, а на третій – на 17 книжок менше, ніж на першій і на другій полицях разом. Запиши у вигляді виразу кількість книжок на трьох полицях разом. Обчисли при
-
Спрости вираз
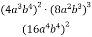 та знайди його значення при
та знайди його значення при 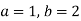 .
.
1

про публікацію авторської розробки
Додати розробку