Посібник для уроків геометрії І семестр 11 класу

Ківерцівська експериментальна школа

 

 

 

 

 

 

 

 

 

Навчальний посібник

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

___________________________________

___________________________________

 

 

 

 

 

 

Шановні одинадцятикласники!

 Вам пропонується навчальний посібник, який ви будете використовувати на уроках геометрії.

Посібник складається з трьох тем. Кожна тема має таку структуру:

• перший урок – урок розбору блоку навчальної інформації;
• наступні уроки – уроки фронтального опрацювання матеріалу, на яких проводиться робота з засвоєння понять, термінів і правил блоку навчальної інформації, також наведені вправи і завдання для відпрацювання практичних умінь і навичок.
• між уроками фронтального опрацювання ви будете виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені
• в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен покаже свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

 

 

Нехай Бог посилає вам мудрості у вивченні геометрії!!!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема №1. Многогранники. Призма

Урок №1

Многогранники. Призма

Геометрія є пізнання всього існуючого

Платон

Питання

1. Многогранники. Призма.
2. Паралелепіпед.

Література

Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, частина 2, §1 – 2, стор. 173 – 195.

1. Многогранники. Призма
1.1	Многогранником називається тіло, поверхня якого складається зі скінченної кількості плоских многокутників.
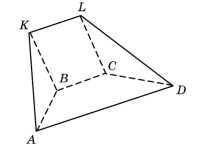
1.2	Призмою називається многогранник, у якого дві грані рівні (їх називають основами) та їх відповідні сторони паралельні, а інші грані (бічні) – паралелограми, у кожного з яких дві протилежні сторони є сторонами основ.
1.3	Призму називають – кутною, якщо її основою є – кутник.
1.4	Перпендикуляр, проведений з деякої точки однієї основидо площини іншої основи, називають висотою призми.		– чотирикутна призма – висота призми - діагональ призми
1.5	Відрізок, що сполучає дві вершини призми, які не належать одній грані, називають діагоналлю призми.
1.6	Якщо бічні ребра перпендикулярні до основ, то кажуть, що призма пряма. Бічні грані прямої призми – прямокутники, а висота прямої призми дорівнює її бічному ребру. Всі інші призми – похилі
1.7	Пряму призму називають правильною, якщо її основи – правильні многокутники.
1.8	Площа бічної поверхні прямої призми дорівнює добутку периметра основи на довжину бічного ребра, яке є висотою призми:
1.9	Площа повної поверхні будь – якої призми дорівнює сумі площі бічної поверхні і площ двох основ:
1.10	– кутна призма має
1.11	Діагональним перерізом призми називають її переріз площиною, яка проходить через паралельні діагоналі основ цієї призми. Діагональний переріз призми – паралелограм
2. Паралелепіпед
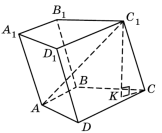
2.12	Призма, основою якої є паралелограм, називається паралелепіпедом.
2.13	Властивості паралелепіпеда: 1)Протилежні грані паралелепіпеда паралельні і рівні; 2) Усі діагоналі паралелепіпеда перетинаються в одній точці (центрі паралелепіпеда) і поділяються нею навпіл
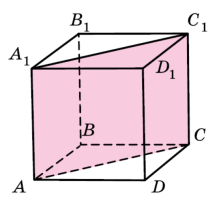
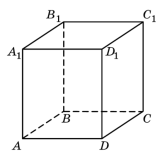
2.14	Прямокутним паралелепіпедом називають прямий паралелепіпед, основою якого є прямокутник.
2.15	Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів.
2.16	Усі чотири діагоналі прямокутного паралелепіпеда рівні.
2.17	Прямокутний паралелепіпед, усі три виміри якого рівні, називається кубом

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уроки №2, 3

«…з усіх втрат втрата часу найтяжча...»
  Григорій Сковорода

 

Фронтальне опрацювання матеріалу

 

Призма

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити тези 1.1 – 1.11 блоку № 1.
2. Усно дати відповідь на питання:

1. Дайте визначення многогранника.
2. Що називається призмою?
3. Що називають діагональним перерізом призми?
4. Чому дорівнює площа бічної поверхні призми?
5. Яка призма називається прямою? правильною?
6. Чому дорівнює площа бічної поверхні прямої призми? площа повної поверхні будь якої призми?
7. Що називають висотою призми? Діагоналлю?
8. У якому співвідношенні перебувають грані, ребра і вершини призми?

 

Завдання 2.

Усно виконати вправи:

1. Скільки граней має семикутна призма?

 

А	Б	В	Г	Д
5	6	7	9	Інша відповідь

 

2. Скільки ребер має чотирикутна призма?

 

А	Б	В	Г	Д
3	21	9	12	Інша відповідь

 

ІІ. Відпрацювання практичних умінь та навичок

 

Завдання 3.

Письмово виконати вправи:

1. Основою прямої призми є квадрат зі стороною 4 см. Знайдіть діагоналі призми, якщо її бічне ребро дорівнює 7 см.
2. Основою прямої призми є ромб з гострим кутом 60° і стороною 8 см. Знайдіть діагоналі призми, якщо її бічне ребро дорівнює 4 см.
3. Сторона основи правильної чотирикутної призми 4 см, а діагональ призми утворює з бічною гранню кут 30°. Знайдіть висоту призми і кут, який утворює діагональ призми з її основою.
4. Основою прямої призми є прямокутний трикутник, гіпотенуза якого дорівнює 8 см, а гострий кут – 30°. Через катет трикутника, який лежить проти кута 30°, проведено переріз, який утворює кут 60° з площиною основи і перетинає бічне ребро. Знайдіть площу перерізу.

 

Завдання 4.

Письмово виконати вправи:

1. Знайдіть площу повної поверхні прямої призми, основою якої є рівнобедрений трикутник з основою 8 см і висотою, проведеною до неї, рівною 3 см, якщо висота призми дорівнює 6 см.
2. Площа бічної поверхні правильної чотирикутної призми дорівнює 64 см ², а площа повної поверхні – 96 см ². Знайдіть висоту призми.
3. Основою прямої призми є ромб з діагоналями 16 см і 30 см, а діагональ бічної грані призми утворює з площиною основи кут 60°. Знайдіть площу бічної поверхні призми.
4. Радіус кола, описаного навколо основи правильної трикутної призми, дорівнює см. Знайдіть площу повної поверхні призми, якщо всі її бічні грані – квадрати.

 

 

 

Уроки №4, 5

«Джерело скаламучене чи зіпсутий потік –

це справедливий, що схиляється перед безбожним»

Книга приповістей Соломонових 25:26

 

Фронтальне опрацювання матеріалу

 

Паралелепіпед

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити тези 2.12 – 2.17 блоку № 1.
2. Усно дати відповідь на питання:

1. Що називається паралелепіпедом?
2. Сформулювати властивості паралелепіпеда.
3. Який паралелепіпед називається прямокутним?
4. Сформулювати властивість діагоналі прямокутного паралелепіпеда.
5. Що таке куб?

 

ІІ. Відпрацювання практичних умінь та навичок

 

Завдання 2

Письмово виконати вправи:

1. В прямокутному паралелепіпеді сторони основи дорівнюють 12 см і 5 см. Діагональ паралелепіпеда утворює з площиною основи кут  45⁰. Знайдіть бічне ребро паралелепіпеда.
2. Основою прямого паралелепіпеда є ромб з діагоналями 10 см и 24 см, а висота паралелепіпеда 10 см. Знайдіть більшу діагональ паралелепіпеда.
3. Через два протилежних ребра куба проведено переріз, площа якого дорівнює 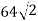см². Знайдіть ребро куба і його діагональ.

 

 

 

 

Завдання 3

Письмово виконати вправи:

3.1. Сторони основи прямого паралелепіпеда дорівнюють 8 см і 15 см і утворюють кут 60⁰. Менша із    площ діагональних перерізів дорівнює 130 см². Знайдіть площу поверхні паралелепіпеда.

3.2. Основою прямокутного паралелепіпеда є квадрат. Діагональ паралелепіпеда утворює з площиною бічної грані кут 30⁰. Знайдіть кут між діагоналлю паралелепіпеда і площиною основи.

3.3. Сторони основи прямого паралелепіпеда дорівнюють 4 см і 8 см, а кут між ними – 60°. Більша діагональ основи дорівнює меншій діагоналі паралелепіпеда. Знайдіть площу бічної поверхні паралелепіпеда.

 

Готуємось до індивідуального опрацювання матеріалу

1. Ребро куба дорівнює 8 см. Знайдіть площу бічної поверхні куба.
2. Бічне ребро прямої призми дорівнює 5 см, а в основі лежить прямокутний трикутник з катетами 3 см і 4 см. Знайти площу повної поверхні призми.
3. Сторони основи прямого паралелепіпеда дорівнюють 3 см і 6 см, а кут між ними – 60°. Більша діагональ основи дорівнює меншій діагоналі паралелепіпеда. Знайдіть площу бічної поверхні паралелепіпеда.

 

 

 

Урок №7

«І як бажаєте, щоб вам люди чинили,

 так само чиніть їм і ви»

Євангелія від Луки 6:31

 

Внутрішньопредметне узагальнення матеріалу

 

Многогранники. Призма

 

І. Засвоєння термінології до теми

Завдання 1.

1. Повторити блок № 1.
2. Письмово відповісти на питання, запропоновані вчителем.

 

ІІ. Узагальнення практичних умінь та навичок

 

Завдання 2.

Усно розв’язати вправи:

1. Вкажіть можливе для призми число: а) ребер;  б) вершин.

 

А	Б	В	Г	Д
17	19	24	33	29

 

2. Знайдіть діагональ прямокутного паралелепіпеда, якщо його лінійні виміри дорівнюють 1 см, 4 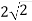см, см.

 

А	Б	В	Г	Д
1 см	см	см	4 см	см

 

3. Ребро куба дорівнює 4 см. Знайти площу:  а) повної поверхні куба; б) бічної поверхні куба.

 

А	Б	В	Г	Д
				Інша відповідь

 

ІІ. Узагальнення практичних умінь та навичок

 

Завдання 3.

Письмово розв’язати вправи:

1. Знайдіть площу найбільшої грані прямокутного паралелепіпеда, якщо його два лінійні виміри дорівнюють 12 см і 14 см, а діагональ паралелепіпеда – 22 см.
2. Площа основи правильної чотирикутної призми 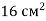, а її бічне ребро 5 см. Знайти площу бічної поверхні призми.
3. Обчисліть площу бічної поверхні прямої призми, в основі якої лежить ромб з діагоналями  2 см і 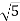см, а менша діагональ призми утворює з площиною основи кут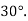
4. Знайдіть площу бічної поверхні прямого паралелепіпеда, в основі якого лежить ромб зі стороною 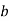і гострим кутом β, а менша діагональ паралелепіпеда нахилена до площини основи під кутом α.
5. Знайдіть площу бічної поверхні прямого паралелепіпеда, в основі якого лежить ромб зі стороною 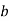і тупим кутом β, а більша діагональ паралелепіпеда нахилена до площини основи під кутом α.

 

 

 

 

 

 

 

 

 

 

 

 

Тема №2. Піраміда. Правильні многогранники

Урок №1

 

Піраміда. Правильні многогранники

« Більше думай, а тоді вирішуй. Спіши повільно!»
   Григорій Сковорода
 

Питання

1. Піраміда.
2. Елементи піраміди.
3. Правильна піраміда.
4. Положення висоти у деяких видах пірамід.
5. Правильні многогранники.

 

Література

Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, частина 2, §3 – 4, стор. 195 – 214.

1. Піраміда
1.1	Пірамідою називається многогранник, у якого одна із граней – довільний многокутник  (її називають основою), а інші грані – трикутники зі спільною вершиною.
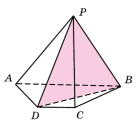
1.2	Піраміда називається n-кутною, якщо її основою є n-кутник. Трикутну піраміду називають також тетраедром.
2. Елементи піраміди
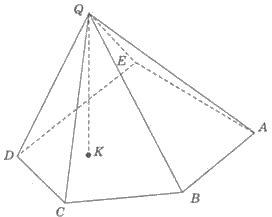
2.3	Висота – перпендикуляр, опущений з вершини піраміди на площину основи (QK).
2.4	Бічні грані – трикутники ABQ, BCQ, CDQ, …
2.5	Бічні ребра –  відрізки, що сполучають вершину  піраміди з вершинами основи (QA, QB, QC,…).
2.6	Площа бічної поверхні піраміди дорівнює сумі площ її бічних граней.
2.7	Площа повної поверхні піраміди дорівнює сумі площі бічної поверхні і площі основи.
3. Правильна піраміда
3.8	Піраміда називається правильною, якщо її основа – правильний многокутник, а основа висоти піраміди співпадає з центром цього многокутника.
3.9	Віссю правильної піраміди називається пряма, яка містить висоту піраміди.
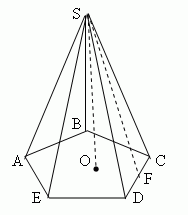
3.10	Апофемою правильної піраміди називається висота бічної грані (SF)
3.11	Площа бічної поверхні правильної піраміди дорівнює добутку півпериметра основи на апофему.
3.12	Переріз піраміди, який проходить через два бічних ребра, що не належать одній грані, називають діагональним перерізом. Діагональні перерізи піраміди – трикутники, однією з вершин яких є вершина піраміди, а протилежна її сторона – діагональ основи.
4. Положення висоти у деяких видах пірамід
4.13	Вершина піраміди проектується в центр описаного навколо основи кола, якщо: бічні ребра рівні; всі бічні ребра утворюють рівні кути з площиною основи;  всі бічні ребра утворюють рівні кути з висотою піраміди.
4.14	Вершина піраміди проектується в центр вписаного в основу  кола, якщо: якщо бічні грані однаково нахилені до основи; якщо висоти бічних граней рівні; якщо висоти бічних граней утворюють рівні кути з  висотою піраміди.
5. Правильні многогранники
5.15	Опуклий многогранник називається правильним, якщо всі грані є рівними правильними многокутниками і в кожній вершині многокутника сходиться одне і те саме число ребер.
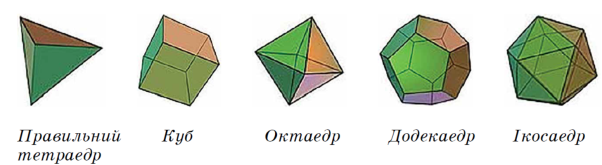
5.16	Існує лише п’ять правильних многогранників: 1) правильний тетраедр (чотиригранник): поверхня – 4 правильні трикутники; 2) куб (шестигранник): поверхня – 6 квадратів; 3)  октаедр (восьмигранник): поверхня – 8 правильних трикутників; 4) додекаедр (дванадцятигранник): поверхня – 12 правильних п’ятикутників; 5) ікосаедр (двадцятигранник): поверхня – 20 правильних трикутників.

 

Уроки  №2 – 4

«Бери вершину i матимеш середину»
  Григорій Сковорода

 

Фронтальне опрацювання матеріалу

 

Піраміда

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повтори тези 1.1 – 5.16 блоку № 2.
2. Усно дай відповідь на питання:

1. Що називають пірамідою?
2. Дати означення висоти, бічного ребра, бічної грані піраміди.
3. Чому дорівнює площа бічної та повної поверхні піраміди?
4. Яка піраміда називається правильною?
5. Що таке вісь правильної піраміди?
6. Що таке апофема?
7. Чому дорівнює площа бічної поверхні правильної піраміди?
8. Коли вершина піраміди проектується у центр кола, вписаного в основу піраміди?
9.  Коли вершина піраміди проектується у центр кола, описаного навколо основи піраміди?
10. Які існують правильні многогранники?

 

3. Ознайомся з історичною довідкою.

Історична довідка

Найбільша з єгипетських пірамід – піраміда Хеопса. Вона була побудована  6000 років тому. Підраховано, що на її будівництво пішло 2 млн. 300 тис. обтесаних вапнякових каменів вагою близько 2,5 т кожен; загальна її вага 5 млн. 750 тис. тонн, висота 146, 6 м, що вище                       40-поверхового будинку, а кожна з 4 її стін тягнеться на 230 м. Припускають, що її будували 20 років 100 тис. рабів, які замінялися кожних  три місяці. З її каменів можна було б побудувати сучасне місто з населенням у 120 тис. чол.

 

ІІ. Відпрацювання практичних умінь та навичок

 

Письмово розв’яжи вправи:

Завдання 2.

1. Основою піраміди є ромб, сторона якого дорівнює 5 см, а одна з діагоналей – 8 см. Знайдіть бічні ребра піраміди, якщо її висота проходить через точку перетину діагоналей основи і дорівнює       7 см.
2. Основою піраміди DABC є трикутник АВС, у якого 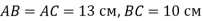, ребро AD перпендикулярне до площини основи і дорівнює 9 см. Знайти площу бічної поверхні піраміди.
3. Основою піраміди DABC є прямокутний трикутник АВС, у якого гіпотенуза АВ = 29 см, катет     АС = 21 см. Ребро AD перпендикулярне до площини основи і дорівнює 20 см. Знайти площу бічної поверхні піраміди.

 

 

Завдання 3.

1. Основою піраміди PABC є прямокутний трикутник з гіпотенузою ВС. Бічні ребра піраміди рівні, а її висота дорівнює 12 см. Знайти бічне ребро піраміди, якщо ВС = 10 см.
2. Сторона основи правильної трикутної піраміди дорівнює 2 см, а бічна грань утворює з площиною основи кут 30°. Знайдіть площу повної поверхні піраміди.
3. Апофема правильної чотирикутної піраміди дорівнює 8 см, а радіус кола, вписаного в основу, –   3 см. Знайдіть площу повної поверхні піраміди.

 

Завдання 4.

1. Основою піраміди є прямокутник зі сторонами 6 см і 8 см. Знайдіть площу бічної поверхні піраміди, якщо її висота дорівнює 4 см, а всі бічні ребра рівні.
2. Основою піраміди є рівнобедрений трикутник з основою 18 см і бічною стороною 15 см. Дві бічні грані, що містять рівні сторони основи, перпендикулярні до площини основи, а їх спільне бічне ребро дорівнює 5 см. Знайдіть площу бічної поверхні піраміди.
3. Виконати вправи 4.3; 4.7 ст. 209 – 210.

 

 

Готуємось до індивідуального опрацювання матеріалу

1. В основі піраміди лежить прямокутник, діагональ якого дорівнює      5 см. Усі бічні ребра піраміди рівні. Знайдіть бічне ребро піраміди, якщо її висота дорівнює 6 см.
2. Знайдіть площу повної поверхні правильної чотирикутної піраміди, у якій сторона основи дорівнює 3 см, а бічна грань нахилена до основи під кутом 60°.
3. Знайдіть висоту піраміди, в основі якої лежить рівнобедрений трикутник зі сторонами 10см, 10см і 12см, а всі двогранні кути при сторонах основи дорівнюють по 60°.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №6

«...найкраща помилка та, яку допускають при навчанні»
   Григорій Сковорода

Внутрішньопредметне узагальнення матеріалу

 

Піраміда. Правильні многогранники

 

І. Засвоєння термінології до теми

Завдання 1.

1. Повторити блок № 2.
2. Письмово дати відповідь на питання, запропоновані вчителем.

 

ІІ. Узагальнення практичних умінь та навичок

Завдання2.

Усно виконати вправи:

1. Знайдіть площу бічної поверхні правильної трикутної піраміди, якщо сторона основи дорівнює    4 см, а апофема – 1 см.

 

А	Б	В	Г	Д
2 см ²	4 см ²	4,5 см ²	6 см ²	Інша відповідь

 

2. Якщо в основі піраміди лежить прямокутний трикутник і всі її бічні ребра однаково нахилені до площини основи, то вершина піраміди проектується в:

 

А	Б	В	Г	Д
точку перетину медіан основи	точку перетину бісектрис основи	середину гіпотенузи	вершину прямого кута	Інша відповідь

 

3. У піраміді проведено переріз площиною, яка паралельна основі та проходить через середину висоти. Знайдіть площу перерізу, якщо площа основи дорівнює 48 см ².

 

А	Б	В	Г	Д
				Інша відповідь

 

Завдання 3.

Письмово виконати вправи:

1. У правильній трикутній піраміді бічне ребро дорівнює 8 см і утворює з площиною основи кут 30º. Знайдіть висоту піраміди.

 

2. Висота правильної чотирикутної піраміди дорівнює 9 см, а бічне ребро – 15 см. Знайти сторону основи піраміди.

 

3. Знайти площу повної поверхні правильної чотирикутної піраміди, висота якої дорівнює   4 см, а апофема – 5 см.

 

4. Основою піраміди є рівнобедренний прямокутний трикутник, катет якого дорівнює 4 см. Бічні грані піраміди, що містять катети трикутника, перпендикулярні до площини основи, а третя грань утворює з площиною основи кут 45. Знайдіть площу повної поверхні піраміди.

Тема №3. Тіла обертання. Циліндр

Урок №1

Тіла обертання. Циліндр

                          

«Математика і поезія це…вираження тієї

                                                                                                                               самої сили уяви, тільки в першому разі уява  звернена до голови, а в другому – до серця»

Теодор Хілл, американський математик

Питання

1. Тіла і поверхні обертання.
2. Циліндр.
3. Площа поверхні циліндра.

Література

Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, частина 2, §5, 11, стор. 216 – 224, 277 – 278.

1. Тіла і поверхні обертання
1.1	Будь – яке тіло, отримане обертанням плоскої фігури (разом з усіма її внутрішніми точками) навколо осі обертання, називають тілом обертання.
1.2	Якщо розглядати обертання плоскої фігури без її внутрішніх точок, отримаємо просторову фігуру обертання або поверхню обертання.
2. Циліндр
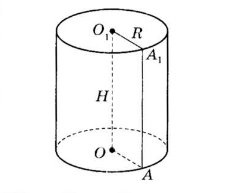
2.3	Циліндром називають геометричне тіло, утворене обертанням прямокутника навколо осі, яка містить одну з його сторін Круги – основи циліндра.	- вісь та висота; А – твірна; ОА – радіус основи
2.4	Відрізки, які сполучають відповідні точки кіл основ, називають твірними.
2.5	Множину всіх твірних називають бічною поверхнею циліндра.
2.6	Висотою циліндра називається відстань між його основами, тобто перпендикуляр, проведений з довільної точки однієї основи до другої основи.
2.7	Перерізи циліндра площинами
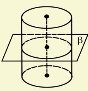
	1. Січна площина паралельна основам (тобто перпендикулярна до осі) – в перерізі маємо круг, що дорівнює основам.
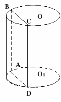
	2. Січна площина проходить через вісь (осьовий переріз) – в перерізі  – прямокутник, дві сторони якого –  твірні, а дві інші – діаметри основ.
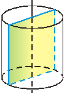
	3. Січна площина паралельна осі – в перерізі прямокутник, дві сторони якого – твірні, а дві інші – паралельні і рівні між собою хорди основ.
2.8	Циліндр, осьовим перерізом якого є квадрат, називають рівностороннім.
3. Площа поверхні циліндра
3.9	Площа бічної поверхні циліндра обчислюється за формулою , де R – радіус основи, H - висота
3.10	Площа повної поверхні циліндра обчислюється за формулою , де R – радіус основи, H - висота

 

 

 

Уроки №2 – 4

«...охота – мати праці, праця все перемагає»
   Григорій Сковорода

Фронтальне опрацювання матеріалу

 

Циліндр. Перерізи циліндра

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повтори тези 1.1 – 2.8 блоку № 3.
2. Усно дай відповідь на питання:

1. Що називають тілом обертання?
2. Що називають фігурою обертання або поверхнею обертання?
3. Що називають циліндром?
4. Що є основами циліндра?
5. Що називають: висотою циліндра? Твірною циліндра?
6. Які властивості мають  твірні циліндра? Висота циліндра?
7. Який циліндр називають рівностороннім?
8. Що ви знаєте про перерізи циліндра площиною?

 

ІІ. Відпрацювання практичних умінь та навичок

 

Завдання 2.

Усно виконати вправи:

1. Знайдіть діагональ осьового перерізу циліндра, якщо радіус основи 1,5 м,  а висота – 4 м.
2. Осьовим перерізом циліндра є квадрат, площа якого дорівнює 64 см ². Знайдіть:

       1) висоту циліндра; 2) радіус основи циліндра.

 

Завдання 3.

Письмово виконати вправи:

Завдання 3.

1.          Зобразіть циліндр, на його бічній поверхні позначте точки А і В. Побудуйте точку перетину прямої АВ з площиною нижньої основи циліндра. Запишіть алгоритм побудови.
2.          Зобразіть циліндр, на його бічній поверхні позначте точки А, В і С. Побудуйте точку перетину площини АВС з площиною нижньої основи циліндра. Запишіть алгоритм побудови.
3.          Знайдіть площу осьового перерізу циліндра, якщо його радіус дорівнює 8 см, а висота – 12 см.
4.          Діагональ осьового перерізу циліндра дорівнює 39 см. Знайдіть: 1) радіус основи циліндра, якщо його висота дорівнює 15 см; 2) висоту циліндра, якщо його радіус дорівнює 18 см.
5.          Квадрат з діагоналлю 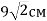обертається навколо однієї зі сторін. Знайдіть площу осьового перерізу утвореного циліндра.
6.          У циліндрі паралельно до його осі проведено переріз, діагональ якого дорівнює 51 см. Висота циліндра дорівнює 45 см, а радіус основи – 15 см. На якій відстані від осі проведено цей переріз?
7.          У циліндрі на відстані 24 см від його осі і паралельно до неї проведено переріз, діагональ якого дорівнює 39 см. Обчисліть радіус основи циліндра, якщо його висота дорівнює 15 см.
8.          Кінці відрізка АВ лежать на колах основ циліндра. Радіус циліндра дорівнює r, його висота – h, відстань між прямою АВ і віссю циліндра дорівнює d. Знайдіть h, якщо r=10дм, d=8дм, АВ=13дм.

 

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

 

Завдання 4.

Письмово виконати вправи:

1. У циліндр вписано правильну трикутну призму, а навколо нього описано правильну шестикутну призму. Знайдіть відношення площ бічних поверхонь цих призм.
2. Основою прямої призми є рівнобедрений прямокутний трикутник. Висота призми дорівнює 10 см, а площа бічної поверхні – 40 см ². Знайдіть радіус основи циліндра, описаного навколо цієї призми.

 

 

 

Уроки №5, 6

«Хто любить навчання, той любить

пізнання, а хто докір ненавидить, той нерозумний»

Книга Приповістей Соломонових, 12 : 1

 

Фронтальне опрацювання матеріалу

 

Площа поверхні циліндра

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити блок № 3.
2. Усно відповісти на питання:

1. Що називають тілом обертання?
2. Що називають фігурою обертання або поверхнею обертання?
3. Що називають циліндром?
4. Що називають: висотою циліндра? Твірною циліндра?
5. Які властивості мають  твірні циліндра? Висота циліндра?
6. Який циліндр називають рівностороннім?
7. Що ви знаєте про перерізи циліндра площиною?
8. За якою формулою обчислюється площа бічної поверхні циліндра?
9. За якою формулою обчислюється площа повної поверхні циліндра?

 

Завдання 2.

Усно виконати вправи:

2.1. Обчисліть площу бічної поверхні циліндра, висота якого дорівнює 14 см, а радіус основи – 4 см.

 

А	Б	В	Г
112π см ²	56π см ²	224π см ²	22π см ²

 

2.2. Обчисліть площу бічної поверхні циліндра, діаметр основи якого дорівнює 4 см, а твірна – 9 см.

 

А	Б	В	Г
36π см ²	72π см ²	12π см ²	24π см ²

 

2.3. Чи правильне твердження: «Щоб знайти площу бічної поверхні циліндра, зовсім не обов’язково знати радіус основи R і висоту H. Досить знати площу осьового перерізу циліндра»?

 

ІІ. Відпрацювання практичних умінь та навичок

 

Письмово виконати вправи:

 

Завдання 3.

1. Осьовим перерізом циліндра є прямокутник зі сторонами 10 см і 6 см. Більша сторона прямокутника є твірною циліндра. Знайти площу бічної поверхні циліндра.
2. Знайти повну поверхню циліндра, радіус якого 2 см, а висота – 3 см.
3. Радіус основи циліндра у 4  рази менший від його висоти, а площа бічної поверхні циліндра дорівнює 288π см ². Знайдіть висоту циліндра і радіус його основи.
4. У циліндрі паралельно його осі проведено переріз, який є квадратом зі стороною 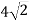см і відтинає від кола основи дугу у 60º. Знайдіть площу повної поверхні циліндра.
5. Відрізок, кінці якого лежать на колах різних основ циліндра, утворює з площиною основи кут 60º і віддалений від осі циліндра на 15 см. Знайдіть площу бічної поверхні циліндра, якщо його висота дорівнює 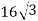  см.

 

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

 

Завдання 4.

 

1.          Діагональ осьового перерізу циліндра дорівнює 40 см. Знайдіть площу бічної поверхні циліндра, якщо його висота удвічі більша від радіуса основи.
2.          Знайдіть площу бічної поверхні циліндра, якщо діагональ розгортки цієї поверхні дорівнює  10 см і утворює кут 30º з твірною циліндра.

 

                                                                                                                                                                                                 

 

 

Урок №7

«Хто любить навчання, той любить

пізнання, а хто докір ненавидить, той нерозумний»

Книга Приповістей Соломонових, 12 : 1

 

Фронтальне опрацювання матеріалу

 

Циліндр. Площа поверхні циліндра

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити блок № 3.
2. Усно відповісти на питання:

1. Що називають тілом обертання?
2. Що називають фігурою обертання або поверхнею обертання?
3. Що називають циліндром?
4. Внаслідок обертання якої фігури утворюється циліндр?
5. Що називають: висотою циліндра? Твірною циліндра?
6. Які властивості мають  твірні циліндра? Висота циліндра?
7. Який циліндр називають рівностороннім?
8. Що ви знаєте про перерізи циліндра площиною?
9. За якою формулою обчислюється площа бічної поверхні циліндра?
10. За якою формулою обчислюється площа повної поверхні циліндра?

 

ІІ. Відпрацювання практичних умінь та навичок

 

Завдання 2.

Письмово виконати вправи:

1. Знайдіть площу осьового перерізу циліндра, якщо його радіус дорівнює 3 см, а висота – 8 см.
2. Діагональ осьового перерізу циліндра дорівнює 13 см. Знайдіть висоту циліндра, якщо його радіус дорівнює 6 см.
3. Квадрат з діагоналлю 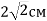обертається навколо однієї зі сторін. Знайдіть площу повної поверхні циліндра.
4. У циліндрі на відстані 8 см від його осі і паралельно до неї проведено переріз, діагональ якого дорівнює 13 см. Обчисліть радіус основи циліндра, якщо його висота дорівнює 5 см.

 

 

 

Готуємось до індивідуального опрацювання матеріалу

1. Знайдіть площу осьового перерізу циліндра, якщо його радіус дорівнює 6 см, а висота – 8 см.
2. Діагональ осьового перерізу циліндра дорівнює 17 см. Знайдіть радіус основи  циліндра, якщо його висота дорівнює 15 см.
3. Квадрат з діагоналлю 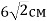обертається навколо однієї зі сторін. Знайдіть площу повної поверхні циліндра.
4. У циліндрі на відстані 3 см від його осі і паралельно до неї проведено переріз, діагональ якого дорівнює 17 см. Обчисліть радіус основи циліндра, якщо його висота дорівнює 15 см.

 

 

Урок №9

«Без роботи день роком стає»

Українське прислів’я

 

Внутрішньопредметне узагальнення матеріалу

 

Тіла обертання. Циліндр

 

І. Засвоєння термінології до теми

 

Завдання 1.

1. Повторити блок № 4.
2. Письмово дати відповіді на питання, запропоновані вчителем.

 

ІІ. Узагальнення практичних умінь і навичок

 

Письмово розв’язати вправи

 

Завдання 2.

 

1. Діагональ осьового перерізу циліндра дорівнює 20 см. Знайдіть площу цього перерізу, якщо радіус циліндра дорівнює 6 см.

 

2. Діагональ осьового перерізу циліндра дорівнює 5 см. Знайдіть площу цього перерізу, якщо висота циліндра дорівнює 3 см.

 

3. Осьовим перерізом циліндра є квадрат, площа якого дорівнює 25 см ². Знайдіть:         1) висоту циліндра; 2) радіус основи циліндра.

 

4. Осьовим перерізом циліндра є квадрат, периметр якого дорівнює 8 см. Знайдіть:         1) висоту циліндра; 2) радіус основи циліндра.

 

5. Знайдіть периметр осьового перерізу циліндра, діагональ якого утворює з твірною циліндра кут 30 ◦ і дорівнює 12 см.

 

6. У циліндрі паралельно до його осі проведено переріз, діагональ якого дорівнює 17 см. Висота циліндра дорівнює 15 см, а радіус основи – 5 см. На якій відстані від осі проведено цей переріз?

 

7. У циліндрі паралельно його осі проведено переріз, який є квадратом зі стороною 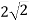см і відтинає від кола основи дугу у 60º. Знайдіть площу повної поверхні циліндра.

 

 

Тема №4. Конус

Урок №1

 

Конус                          

«Геометрія є пізнання всього існуючого»

Платон

                                                                                                                                                                                                 

Питання

1. Конус.
2. Площа поверхні конуса.

Література

Істер О.С. Математика: (Алгебра та початки аналізу і геометрія, рівень стандарту): Підручник для 11 класу закладів загальної середньої освіти. – Київ: Генеза, 2019 рік, частина 2, §6, 11, стор. 225 – 232, 278 – 279.

1. Конус
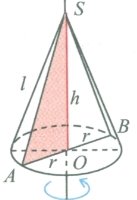
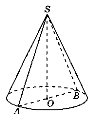
1.1.	Конусом називають геометричне тіло, утворене обертанням прямокутного трикутника навколо осі, що містить один з його катетів. Основа конуса – круг.	SО – вісь і висота; SА – твірна; ОА – радіус основи
1.2	Відрізок, що сполучає вершину конуса з точками кола основи називаються твірною конуса.
1.3	Множину всіх твірних називають бічною поверхнею конуса.
1.4	Висотою конуса називається перпендикуляр, опущений з вершини конуса на площину основи (відрізок, що сполучає вершину конуса з центром основи).
1.5	Перерізи конуса площинами
	1. Січна площина паралельна основі (тобто перпендикулярна до осі) – в перерізі круг, подібний до основи. Коефіцієнт подібності:
	2. Січна площина проходить через вісь (осьовий переріз) – рівнобедрений трикутник, бічні сторони якого є твірними конуса, а основа – діаметр основи конуса.
	3. Січна площина проходить через вершину конуса і не містить його осі – переріз –  рівнобедрений трикутник, бічні сторони якого твірні, а основа – хорда основи конуса
1.6	Конус, осьовим перерізом якого є правильний трикутник, називають рівностороннім.
2. Площа поверхні конуса
2.7	Площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну.
2.8	Площа повної поверхні конуса дорівнює сумі площі його бічної поверхні і площі основи

 

 

 

Урок №2

«Золоті яблука на срібнім тарелі це слово,

проказане часу свого»

Приповісті Соломонові 25:11

 

Фронтальне опрацювання матеріалу

 

Конус. Перерізи конуса

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторіть тези 1.1 – 1.6 блоку №4.
2. Дайте відповіді на питання:

1. Яку фігуру називають конусом?
2. Дайте визначення твірної та висоти конуса.
3. Внаслідок обертання якої фігури утворюється конус?
4. Що називають бічною поверхнею конуса?
5. Дайте визначення перерізам конуса.
6. Який конус називають рівностороннім?

 

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

 

Завдання 2.

2.1. Висота конуса дорівнює 15 см, а радіус основи дорівнює 8 см. Знайти твірну конуса.

 

2.2. Твірна конуса дорівнює 12 см, нахилена до площини основи під кутом 60⁰. Знайдіть площу основи конуса.

 

2.3. Осьовий переріз  – прямокутний трикутник. Знайдіть площу цього перерізу, якщо радіус основи конуса дорівнює 5 см.

 

2.4. Осьовий переріз конуса правильний трикутник зі стороною 2r. Знайти площу перерізу, проведеного через дві твірні конуса, кут між якими дорівнює 30⁰.

 

 

 

 

Уроки №3, 4

«Хто любить навчання, той любить

пізнання, а хто докір ненавидить, той нерозумний»

Книга Приповістей Соломонових, 12 : 1

 

Фронтальне опрацювання матеріалу

 

Площа поверхні конуса

 

І. Робота над засвоєнням понять, термінів і правил

 

Завдання 1.

1. Повторити блок № 4.
2. Усно дати відповідь на питання:

1. Що називається конусом?
2. Дати означення елементам конуса: твірна, висота, вісь,  бічна поверхня.
3.  Дати означення перерізам конуса: осьового; площиною, паралельною основі; площиною, яка проходить через вершину конуса.
4. Чому дорівнює площа бічної поверхні конуса?
5. Чому дорівнює площа повної поверхні конуса?

 

ІІ. Відпрацювання практичних умінь та навичок

 

Завдання 2.

Письмово розв’язати вправи, стор.281 – 283  підручника, 11.3; 11.7; 11.17; 11.21; 11.37.

 

Завдання 3.

Письмово розв’язати вправи:

1. Осьовий переріз конуса – рівнобедрений  прямокутний трикутник, висота якого проведена до основи, дорівнює 10 см. Знайдіть площу повної поверхні конуса.
2. Площа бічної поверхні конуса дорівнює 32π см², а його висота – 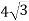см. Знайдіть кут нахилу твірної конуса до площини його основи.
3. Розгортка бічної поверхні конуса – сектор, кут якого дорівнює 240º. Знайди площу повної поверхні конуса, якщо периметр його осьового перерізу дорівнює 48 см.

 

 

 

 

 

Готуємось до індивідуального опрацювання матеріалу

1. Знайдіть площу осьового перерізу конуса, діаметр основи якого дорівнює 24 см, а твірна –  20 см.
2. Перпендикуляр, проведений із центра основи конуса до твірної, ділить її на відрізки 4 см і  25 см, рахуючи від вершини конуса. Знайдіть площу основи  і довжину кола основи конуса.
3. Радіус основи конуса дорівнює 8 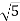см, а відстань від центра його основи до твірної – 16 см. Знайдіть висоту конуса.

 

 

Урок №6

«Щастя не в тому, щоб робити завжди,

що хочеш, а в тому, щоб завжди хотіти

того, що робиш»
Лев Толстой

Внутрішньопредметне узагальнення матеріалу

 

Конус

 

І. Систематизація та узагальнення теоретичних знань

 

Завдання 1.

1. Повторити блок № 4.
2. Письмово дати відповідь на питання, запропоновані вчителем.

 

ІІ. Систематизація та узагальнення практичних умінь та навичок

 

Завдання 2.

Усно розв’язати вправи:

 

1. Відрізок, що сполучає вершину конуса з точкою кола основи є:

 

А	Б	В	Г	Д
Висотою конуса	Радіусом конуса	Твірною конуса	Апофемою	Інша відповідь

 

2. Радіус основи конуса дорівнює 3 см. Знайдіть твірну конуса, якщо його висота дорівнює 4 см.

 

А	Б	В	Г	Д
3 см	4 см	5 см	6 см	Інша відповідь

 

3. Твірна конуса дорівнює 10 см і нахилена до площини основи під кутом 30º. Знайдіть радіус основи конуса.

 

А	Б	В	Г	Д
5 см	см	см	10 см	Інша відповідь

Завдання 3.

Письмово розв’язати вправи:

 

1. Знайдіть площу основи конуса, в якому висота дорівнює 2 см, а твірна становить см.

 

 

2. Знайдіть площу основи конуса, твірна якого дорівнює 12 см, а площа бічної поверхні - 504 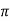см².

 

3. Радіус основи конуса дорівнює 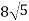см, а відстань від центра його основи до твірної –  16 см. Знайдіть висоту конуса.

 

4. Висота конуса дорівнює 40 см, а відстань від центра його основи до твірної –  24 см. Знайдіть радіус конуса.

 

5. Знайдіть площу повної поверхні конуса, якщо його висота дорівнює 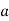, а твірна утворює кут φ з площиною основи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для нотаток

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________