Посібник для уроків курсу за вибором "Математичні смарагди" ІІ семестр

Про матеріал

Посібник містить розробки занять для курсу за вибором у 5 класі "Математичні смарагди" на ІІ семестр

Перегляд файлу

Тема №3 (продовження). Конструювання

Уроки №7, 8

Конструктор «Пентаміно»

Завдання 1.

Дайте відповіді на питання, запропоновані вчителем у презентації.

Завдання 2.

Найбільш відома гра у пентаміно – скласти із всіх фігурок прямокутник, без перекриття і відступів.

2.1. Самостійно замостити прямокутник без підказок. Хто перший справиться із завданням, показує свій варіант вчителю.

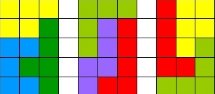
2.2. Самостійно замостити прямокутник без підказок. Хто перший виконає завдання, показує свій варіант вчителю.

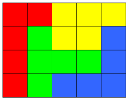
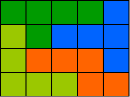
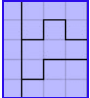
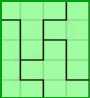
2.3. Складіть всі 12 фігур пентаміно в прямокутник .

Завдання 3.

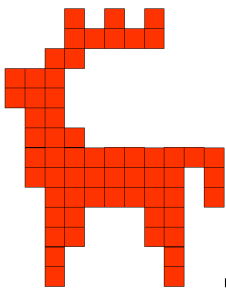
Поділіться на 5 груп. Використовуючи домашні заготовки фігурок пентаміно, складіть зображення тваринок, запропоноване вчителем. Наклейте фігурки на листок паперу або у зошит.

Група 1.

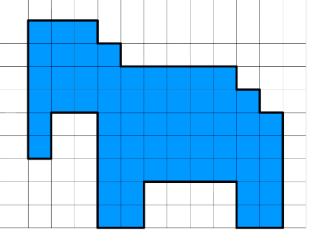
Група 2.

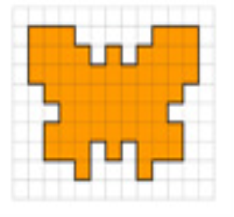
Група 3.

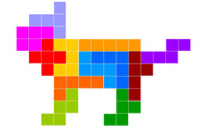
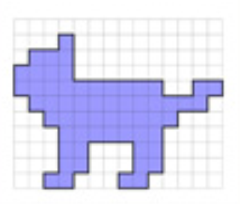
Група 4.

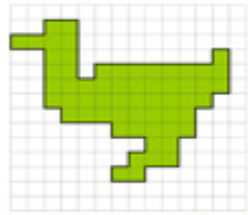
Група 5.

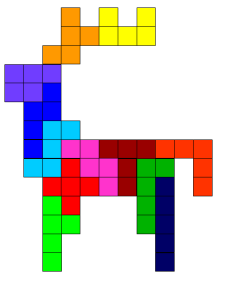
Завдання 4.

Скачати на свій телефон через GooglePlay або AppStore додаток «Пентаміно» і пограти декілька рівнів.

Тема №4. Логічні задачі

Уроки №1, 2

Задачі, що розв’язуються з кінця

Завдання 1.

В класній кімнаті було кілька учнів. Після того, як 7 учнів вийшли і 9 учнів ввійшли в кімнату, їх стало 31 чоловік. Скільки учнів було в кожній кімнаті спочатку?
В коробці лежали сірники. Їх кількість подвоїли, а потім забрали 8 сірників. Остачу подвоїли ізнову забрали 8 сірників. Коли таку операцію повторили третій раз, в коробці не залишилося жодного сірника. Скільки сірників було в коробці спочатку?
Коло мосту через річку зустрілися ледар і лицар. Ледар поскаржився на свою бідність. У відповідь лицар запропонував: ”Я можу тобі допомогти. Кожного разу, коли ти перейдеш цей міст, грошей у тебе збільшиться в 2 рази. Але після кожного переходу ти маєш віддати мені 24 копійки.” Три рази ледар перейшов через міст, а коли заглянув у свій гаманець, він виявився порожнім. Скільки грошей було в ледаря спочатку?
З ринку поверталися дві селянки. Одна з них спитала іншу: «Що ти продавала?» Відповідь була така: «Я продавала дині, і вийшло так, що першому покупцю я продала половину всіх динь і ще півдині, другому – половину решти динь і ще півдині. Третьому покупцю я продала також половину того, що залишилося після другого покупця, і ще півдині. Більше динь в мене не залишилося». Скільки ж динь продала ця селянка?
Мати для трьох синів залишила вранці тарілку слив, а сама пішла на роботу. Першим прокинувся старший син. Побачивши на столі сливи, він з’їв їх третю частину й пішов. Другим прокинувся середній син. Думаючи, що його брати ще сплять, він з'їв третину того, що було на тарілці, й теж пішов. Найпізніше встав молодший син. Побачивши сливи він вирішив, що брати ще не їли їх, і тому з’їв лише третину того, що було на тарілці. Після цього залишилося 8 слив. Скільки всього слив було спочатку?

Розв’язання.
1. Після того, як 7 учнів вийшли і 9 учнів ввійшли в кімнату, їх кількість збільшилася на 9-7=2 (учні) і стала 31 чоловік. Тому спочатку їх було 31-2=29 (чоловік). Інший спосіб: перед тим , як 9 учнів увійшли в кімнату, в ній було 31-9=22 (учні), а перед тим, як 7 учнів вийшли, в ній було 22+7=29 (учнів).

2. Після другого виконання операції в коробці було (0+8):2=4 сірники. Після першого виконання операції було (4+8):2=6 сірників. Спочатку в коробці було (6+8):2=7 сірників.
3. Після другого переходу в ледаря було (0+24):2=12 копійок. Після першого переходу в ледаря було (12+24):2=18 копійок. Спочатку в ледаря було (18+24):2=21 копійок.
4. Після другого покупця в селянки залишилася одна диня (півдині і півдині). Після першого покупця в селянки було півтори дині й півтори дині, тобто три дині. Три з половиною дині – це половина динь, які були спочатку. Отже спочатку було три з половиною і три з половиною, разом 7 динь.

5. Оскільки молодший брат з’їв третину, то залишилося дві третини, які становлять 8 слив. 8:2•3=12 (слив) залишив середній брат. Це дві третини від того, що залишив старший брат. 12:2•3=18 (слив) залишив старший брат. В свою чергу, це дві третини від того, що залишила мама. 18:2•3=27 (слив) залишила мама.

Завдання 2.

Задача 1. Селянин прийшов до царя і запитав: «Царю, дозволь мені взяти з твого садка одне яблуко». Цар відповів: «Мій садок обнесений трьома заборами. В кожному заборі є тільки одні ворота і коло кожних воріт стоїть сторож. Якщо скажеш, скільки яблук треба тобі взяти, щоб виконати наступні умови: першому сторожу віддати половину яблук, які візьмеш, і ще 1 яблуко; другому сторожу віддати половину з тих, що залишилися і ще 1 яблуко; третьому сторожу віддати половину того, що залишилося (після того, як віддаси другому) і ще 1 яблуко, а тобі щоб лишилося 1 яблуко, то я дозволю тобі піти в сад».

Селянин подумав трошки і відповів царю. Цар дозволив йому піти в сад. Яке число назвав селянин ?.

Розв’язання.

Звертаємо увагу на те, що після того, як селянин віддав третьому сторожу половину і ще 1 яблуко в нього залишилося 1 яблуко. Отже 1 + 1 яблуко – це половина.

( 1 + 1 ) х 2 = 4 ( ябл.) було перед тим, як віддати третьому сторожу, або після того, як віддали другому сторожу;

( 4 + 1 ) х 2 = 10 ( ябл.) – було перед тим, як віддати другому сторожу, або після того, як віддали першому сторожу;

( 10 + 1 ) х 2 = 22 ( яб.) – було перед тим, як віддати першому сторожу або треба взяти з садка.

Відповідь: 22 яблука.

Задача 2. Господиня продала першому покупцеві половину груш, які вона мала, та ще 5 груш, другому — половину залишку та ще 3 груші, а третьому покупцеві — половину нового залишку та ще 4 груші. Після цього в неї залишилося 2 груші. Скільки груш було в господині спочатку?

Розв’язання

Таку задачу можна ділити на етапи: перший етап — перший покупець, другий етап — другий покупець, третій етап — третій покупець. Щоб її розв’язати, потрібно почати обчислювати вирази з кінця, змінюючи при цьому ділення на множення, а віднімання на додавання.

1) (2 + 4) • 2 = 12 (груш)

2) (12 + 3) •2 = 30 (груш)

3) (30 + 5) • 2 = 70 (груш)

Відповідь: 70 груш було в господині спочатку.

Завдання 3. Виконайте задачі самостійно.

Задача 1. Магазин першого дня продав половину сувою тканини, другого дня — половину решти, а третього — половину нового залишку й останні 5 метрів. Скільки метрів було в сувої спочатку?

Розв’язання

В цій задачі розв’язання містить три кроки – треба взнати кількість метрів тканини, яка залишалась у магазині, відповідно, на початку третього, другого та першого дня. В першому кроці – дві арифметичні дії, в другому і третьому – одна.

1) (0 + 5) • 2 = 10 (м)

2) 10 • 2 = 20 (м)

3) 20 • 2 = 40 (м)

Відповідь: 40 метрів тканини було у сувої спочатку.

Задача 2. Гра починається із числа 1. За один хід дозволяється помножити наявне число на будь-яке натуральне число від 2 до 9. Виграє той, хто першим одержить число, більше 1000.

(Аналізуючи з кінця, знаходимо виграшні позиції. Це числа від 56 до 111 і від 4 до 6. Таким чином, виграє перший гравець (його перший хід - в 4, 5 або 6).

Уроки №3,4

Старовинні задачі на вгадування чисел

Завдання 1. Розв’язати стародавні задачі.

Задача 1.

Розв’язання.

Задача 2.

Розв’язання.

Задача 3.

Розв’язання.

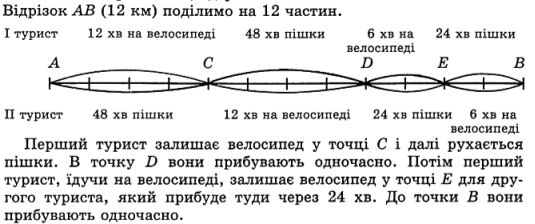
Задача 4.

Розв’язання.

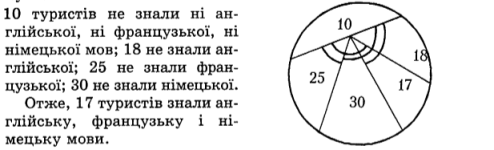
Задача 5.

Розв’язання.

Завдання 2. (домашнє)

Користуючись різними джерелами інформації, підготувати одну стародавню задачу самостійно.

Урок №5

Задачі з правдивими та неправдивими твердженнями

Задача 1. В трьох коробках лежать ручки, олівці та фломастери. На коробках є написи: «Олівці», «Ручки», «Олівці або фломастери». Але всі написи – неправильні. Що насправді лежить у коробці?

Розв’язання

Якщо напис «Олівці або фломастери» неправильна, то в коробці можуть бути лише _______________(ручки). Тоді в коробці з написом «Олівці» лежать _____________________(фломастери), а в коробці з написом «Ручки» - олівці.

Задача 2. Іван-царевич пришов до Кощія Безсмертного визволяти Василісу Прекрасну. Кощій показав йому три темниці, в одній із яких була Василіса, в іншій – Змій Горинич, а третя була порожня. На темницях були написи:

На 1-й – «Тут Василіса Прекрасна»;

На 2-й – «Третя темниця порожня»;

На 3-й – « Тут Змій Горинич».

Іван –царевич знає, що всі написи неправдиві. Допоможіть йому знайти Василісу Прекрасну.

Підказка. Якщо припустити, що Василіса в першій або третій темниці, отримаємо протиріччя.

Задача 3. На безлюдному острові ростуть три дерева: береза, сосна дуб. Під одним із них заритий скарб, а на деревах висять таблички:

На дубі – «Скарб зарито під сосною»;
На березі – «Скарб зарито тут»;
На сосні – «Скарб зарито під березою».

Два написи говорять правду, а один бреше. Де зарито скарб?

Підказка. Написи на двох деревах містять одне і те ж твердження, значить, вони правдиві.

Задачі на пошук «героя» або «злочинця»

У розв’язанні допомагає «метод Шерлока Холмса»: послідовно виключати тих учасників подій, які не могли вчинити даний злочин.

Задача 4. До князя дійшла новина, що один із трьох богатирів вбив Змія Горинича. Богатирі, прийшовши до князя, сказали наступне:

Ілля Муромець: «Змія вбив Добриня Нікітич»;
Добриня Нікітич «Змія вбив Альоша Попович»;
Альоша Попович: «Я вбив Змія».

Відомо, що один з богатирів сказав правду, двоє інших злукавили. Хто вбив Змія Горинича?

Розв’язання:

Ілля Муромець не міг вбити змія, оскільки тоді всі твердження богатирів будуть брехливі;
Альоша Попович теж не міг, оскільки в такому випадку правдиві два твердження і неправдиве одне;
Значить Змія вбив ______________________________, правду сказав тільки ___________________________________, злукавили __________________________

_______________________________________________________________________

Задача 5. Степанку на день народження мама спекла великий торт. Хтось із друзів Степана пожартував і заховав торт. Діти висловили різні думки про те, хто це міг бути.

Борис: «Торт заховав Діма»;
Діма: «Андрій говорить неправду»;
Тарас: «Це був Женя»;
Жора: «Тарас не ховав торта»;
Андрій: «Це не я»;
Женя: «Борис сказав правду»;
Федір: «Це я заховав торт»;
Степан: «Це був Борис».

Тільки одне з цих тверджень виявилось правдивим. Хто ж заховав торт?

Клас ділиться на групи. Кожна група розв’язує одну із задач.

Задача 6. Три дівчинки Алла, Віра і Даша на новорічному балу були в червоному, білому і синьому платтях. Інші учасники балу відмітили:

«Алла була в червоному»;
«Віра була не в червоному»;
«Даша була не в синьому».

Серед цих тверджень лише одне правдиве. В якому плаття була кожна із дівчат?

Задача 7. Чотири дівчинки Соня, Оля, Ріта і Наташа, взявши участь у змаганнях, вибороли чотири місця. Вболівальники почали сперечатись:

«Соня була другою, Оля першою»;
«Оля – друга, Ріта – третя»;
«Ріта – четверта, Наташа – друга».

Відомо, що одна частина кожного із тверджень вірна, а інша – ні. Хто яке місце посів?

Задача 8. П’ять хлопчиків грали у дворі в футбол і розбили м’ячем вікно.

Ваня сказав: «Це Паша або Денис»;
Паша сказав: «Це не я і не Володя»;
Діма сказав: «По-моєму, один із них говорить правду, а інший – ні»;
Володя сказав: «Діма, ти помиляєшся».

Виявилось, що лише один хлопчик висловив невірне твердження. Хто розбив вікно?

Задача 9. В Країні див проводилось слідство по справі про вкрадене борошно. На суді Березневий заєць заявив, що борошно вкрав Капелюшник. В свою чергу, Капелюшник і Соня дали свідчення, які по деяким причинам були незафіксовані. В ході судового слідства виявилось, що борошно вкрав лише один із трьох підсудних і що тільки він дав правдиві свідчення. Хто вкрав борошно?

Домашнє завдання

Знайдіть і запишіть інформацію про те, хто послужив прототипом Шерлока Холмса.

Урок №6

Задачі про рицарів та брехунів

В задачах про рицарів і брехунів відомо, що рицарі завжди говорять правду, а брехуни завжди обманюють. Можливі такі варіанти задач такого типу:

Встановити, хто з героїв є рицарем, а хто брехуном;
Визначити кількість цих героїв;
Вияснити що-небудь, не знаючи, хто перед вами – рицар чи брехун.

Задача 1. На одному острові живуть рицарі і брехуни. Чи може житель острова заявити:

А) «Я брехун»;

Б) «І мій батько, і я – брехуни»?

Розв’язок. А) не може. Якщо цю фразу говорить рицар, значить він бреше; а якщо брехун, значить він говорить правду. І те, і інше неможливо. Ми отримали протиріччя.

Задача 2. Дозволено ставити жителю острова одне питання. Як вияснити, рицар він чи брехун?

Підказка. Поставте питання, на яке точно знаєте відповідь.

Задача 3. На острові є два міста: Правдоград (в ньому живуть лише рицарі) і Кривдинськ (в ньому живуть брехуни). Жителі цих міст часто ходять один до одного в гості. Подорожній зайшов в одне із міст. Як йому вияснити в якому, поставивши лише одне питання перехожому?

Задача 4. Подорожній прибув на роздоріжжя двох доріг, одна із них веде в місто рицарів, а інша – в місто брехунів. Як йому вияснити, яка із доріг веде в місто рицарів, поставивши лише одне питання перехожому?

Розв’язання. Наприклад, можна поставити таке питання: «Якщо я запитаю, чи веде права дорога в місто рицарів, ти відповіси мені «так»?

Складемо таблицю можливих відповідей перехожого в залежності від того, чи веде дорога в місто рицарів і чи є місцевий житель рицарем?

Перехожий	Дорога	Відповідь на питання, чи веде дорога в місто рицарів?	Відповідь на питання подорожнього
Рицар	Веде в місто рицарів	Так	Так
Рицар	Не веде в місто рицарів
Брехун	Веде в місто рицарів	Ні	Так
Брехун	Не веде в місто рицарів

Задача 5. Один із трьох папуг завжди говорить правду, другий завжди береше, а третій – хитрун, тобто інколи говорить правду, а інколи обманює. Кожному із папуг поставили питання: «Кеша – брехун?» Ось що вони відповіли:

Кеша: «Я хитрун!»;
Гоша: «Кеша – брехун!»;
Паша: «Кеша – абсолютно чесний папуга»

Хто ж насправді Кеша? Що можна сказати про інших папуг?

Задача 6. (домашнє завдання)

Подорожній оглядав острів рицарів і брехунів у супроводі місцевого провідника. Побачивши в стороні від дороги жителя острова, подорожній попросив провідника вияснити, хто він. Повернувшись, провідник сказав: «Він говорить, що рицар». Ким був провідник?

Уроки №7, 8

Задачі на переливання

Завдання 1.

Виконати письмово задачі.

Задача 1.Ви маєте 4 циліндричні ємності місткістю 200 мл, 400мл, 600 мл і 800 мл. Ємність із місткістю 400 мл, наповнена молоком, інші - порожні. Користуючись тільки цими ємностями, розлийте молоко так, щоби в кожній ємності було рівно 100 мл молока.

Розв’язання. Використаємо таблицю

Крок	1	2	3	4	5
200 мл	0	200	100	200	100
400 мл	400	200	200	0	100
600 мл	0	0	100	100	100
800 мл	0	0	0	100	100

Задача 2.Розділіть порівну між двома родинами 12 л квасу, що знаходиться в 12-літровому барилі, скориставшись для цього порожніми 8-літровим відром і трилітровою каструлею.

Розв’язання. Використаємо таблицю

Крок	1	2	3	4	5
12 л	12	9	9	6	6
8 л	0	0	3	3	6
3 л	0	3	0	3	0

Задача 3.Як за допомогою 5-літрового бідона і 3 літрової банки набрати з річки 4 л води? Зайву воду можна виливати.

Розв’язання.

Перший спосіб. Здійснюємо переливання з більшої посудини в меншу.

Крок	1	2	3	4	5	6
3 л	0	3	0	2	2	3
5 л	5	2	2	0	5	4

Другий спосіб. Здійснюємо переливання з меншої посудини в більшу.

Крок	1	2	3	4	5	6	7	8
3 л	3	0	3	1	1	0	3	0
5 л	0	3	3	5	0	1	1	4

Задача 4. Маємо дві посудини - 3-літрову й 5-літрову. Користуючись цими посудинами, отримайте 1 л води. Ви маєте водопровідний кран і раковину, куди можна зливати воду.

Розв’язання. Використаємо таблицю

Крок	1	2	3	4
3 л	3	0	3	1
5 л	0	3	3	5

Задача 5.10-літровий бідон наповнений водою. Як за допомогою порожніх 7-літрового й 3-літрового бідонів відміряти 5 літрів води?

Розв’язання. Використаємо таблицю

Крок	1	2	3	4	5	6	7	8	9
10 л	10	3	3	6	6	9	2	2	5
7 л	0	7	4	4	1	1	7	5	5
3 л	0	0	3	0	3	0	1	3	0

Задача 6. Як за допомогою 7-літрової і 11-літрової банок набрати з водопровідного крану 2 літри води? Зайву воду можна виливати.

Розв’язання. Використаємо таблицю

Крок	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
7 л	0	7	0	4	7	0	7	0	1	7	0	5	7	0	7
11 л	11	4	4	11	8	8	1	1	11	5	5	11	9	9	2

Задача 11 . Дядько Федір зібрався їхати до батьків в гості і попросив у кота Матроскина

4 л простоквашинського молока. А в Матроскина лише 2 порожніх бідона: трилітровий

і п'ятилітровий. І восьмилітрове відро, наповнене молоком. Як Матроскину відлити 4 літри молока за допомогою наявних судин?

Розв’язання: Переливаємо з восьмилітрового відра 5 літрів молока в п'ятилітрове. Переливаємо з п'ятилітрового бідона 3 літри в трилітровий бідон. Переливаємо їх тепер у восьмилітрове відро. Отже, тепер трилітрове відро порожнє, у восьмилітровому 6 літрів молока, а в п'ятилітровому - 2 літри молока. Переливаємо 2 літри молока з п'ятилітрового бідона в трилітровий, а потім наливаємо 5 літрів з восьмилітрового відра в п'ятилітровий бідон. Тепер у восьмилітровому 1 літр молока, в п'ятилітровому - 5, а в трилітровому - 2 літри молока. Доливаємо трилітровий бідон з п'ятилітрового і переливаємо ці 3 літри у восьмилітрове відро.

У восьмилітровому відрі стали 4 літри, так само, як і в п'ятилітровому бідоні.

Крок	1	2	3	4	5	6	7	8
8 л	8	3	3	6	6	1	1	4
3 л	0	0	3	0	2	2	3	0
5 л	0	5	2	2	0	5	4	4

Завдання 2.

Самостійно розв’язати задачі.

1 варіант

1.Як розділити 18 л меду порівну між двома бджолярами, використовуючи порожні ємності 13 і 8 літрів?

2.Маємо кран, з якого можна набрати досить багато води, і раковину, щоб зливати зайву воду. Чи можна набрати з крана рівно 2 л води за допомогою 7-літрової банки й 11-літрової банки?

3.Як відміряти 10 л молока, користуючись глечиками ємністю 50 і 30 л?

4.У бочці 20 літрів води. Як за допомогою двох порожніх відер на 7 і 13 л за найменше число переливань набрати 5 л води?

2 варіант

1. Перша посудина вміщує 9 л, друга 5 д, а третя - 3 л. Перша посудина заповнена водою, а інші дві порожні. Як за допомогою цих посудин відміряти 1 л води?

2.Із повної посудини ємністю 13 літрів потрібно відлити 7 л гасу, користуючись двома

порожніми відрами: 4 л і 9 л. Яке це зробити?

3.Є 3-літрова банка соку й дві порожні (літрова і 2-літрова). Як розлити сік так, щоб у всіх банках було по 1л соку?

4.Як з повного бідона ємністю 12 л відлити половину води, користуючись 8 і 5 л?

Завдання 3.

Виконати самостійно інтерактивні вправи, які знаходяться за посиланням

https://cutt.ly/truQbnM

Урок №9

Задачі на зважування

Задача 1. Із трьох однакових монет одна фальшива, і її вага менша ваги справжньої. Як за одне зважування знайти цю монету?

Розв’язування. Позначимо монети номерами: 1, 2, 3. Покладемо на ваги монети 1, 2 і проаналізуємо всі можливі варіанти.

1 і 2	1 і 2	1 і 2
Якщо монета у легша, то монета 1 – фальшива	Якщо ваги в рівновазі, то монета 3 фальшива	Якщо монета 2 легша, то монета 2 – фальшива

Це розв’язування можна записати за допомогою схеми.

Зважування №1	1 і 2(3)
Результат		=
Висновок: фальшива монета	1	3	2

Задача 2. Відомо, що із дев’яти однакових по вигляду монет одна фальшива – її вага менша справжньої. Потрібно за два зважування знайти цю монету. Запишіть розв’язування за допомогою схеми.

Підказка. Цю задачу можна звести до попередньої. Для цього достатньо розбити монети на три однакові групи і вияснити за перше зважування, в якій із груп знаходиться фальшива монета.

Зважування №1	1, 2, 3 і 4, 5, 6 (7, 8, 9)
Результат			=
Висновок: фальшива монета	Серед ____________		Серед ___________		Серед ____________
Зважування №2	1 і 2 (3)
Результат		=		=		=
Висновок: фальшива монета

Задача 3. Із трьох монет одна фальшива, причому невідомо, легша вона чи важча від справжніх. Як знайти її за два зважування і визначити, легша вона чи важча?

Підказка. В задачі 6 варіантів відповідей, оскільки кожна із трьох монет може бути легша або важча.

Зважування №1	1 і 2(3)
Результат			=
Висновок: фальшива монета	__ або ___		_____		__ або ___
Зважування №2	1 і 3 (2)		1 і 3 (2)		1 і 3 (2)
Результат		=		=		=
Висновок: фальшива монета (легка або тяжка)

У випадку рівноваги монет 1 і 2 при першому зважуванні друге зважування дозволить визначити, легша фальшива монета чи важча.
У випадку нерівності монет 1 і 2 перше зважування дозволить визначити, легша фальшива монета чи важча, а друге зважування дозволить знайти фальшиву монету.

Поділити клас на групи. Кожній групі розв’язати одну із запропонованих задач.

Задача 4. Відомо, що із семи однакових за виглядом монет одна фальшива – її вага більша від ваги справжньої. Як за два зважування знайти фальшиву монету?

Задача 5. Відомо, що із 25 однакових за виглядом монет одна фальшива – її вага менша від ваги справжньої. Як за три зважування знайти цю монету?

Задача 6. В коробці лежить 26 діамантів, із яких один природного походження, інші – штучного. Маси штучних діамантів однакові, маса природного – трішки менша. Складіть план дій для знаходження природного діаманта за три зважування.

Домашнє завдання:

Із двох фальшивомонетників перший робить монети важчими від справжніх, а другий – легшими від справжніх. Є 15 однакових за виглядом монет, серед них одна – фальшива. Як за два зважування можна визначити, хто зробив фальшиву монету – перший чи другий?

Зважування №1	1, 2, 3, 4, 5 або 6, 7, 8, 9, 10 (11, 12, 13, 14, 15)
Результат			=
Висновок	Якщо фальшива монета легша, то вона серед ________ Якщо фальшива монета важча, то вона серед ________ Справжні: __________________		Фальшива монет серед _________________ Справжні: __________________		Якщо фальшива монета легша, то вона серед ________ Якщо фальшива монета важча, то вона серед ________ Справжні: __________________
Зважування №2	1, 2, 3, 4, 5 або 6, 7, 8, 9, 10 (11, 12, 13, 14, 15)
Результат		=		=		=
Висновок

Урок №10

Задачі на зважування

Задача 1. Є 4 монети. Скільки потрібно зважувань, щоб знайти серед них найлегшу?

Розв’язання.

Розіб’ємо монети на пари.
В кожній парі виберемо монету, яка легша.
Порівняємо між собою легкі монети кожної із пари.

Запишемо розв’язок за допомогою таблиці.

Зважування №1 і №2	1 і 2, 3 і 4
Результат
Висновок: найлегша монета	Серед 1 і 3		Серед 1 і 4		Серед 2 і 3		Серед 2 і 4
Зважування №3	1 і 3		1 і 4		2 і 3		2 і 4
Результат
Висновок: найлегша монета	1	3	1	4	2	3	2	4

Задача 2. Є 8 різних за вагою пластикових кульок. Як за 10 зважувань визначити найважчу і найлегшу кульку? Запишіть розв’язок за допомогою схеми.

Задача 3. Коваль викував 4 мечі для чотирьох рицарів. Але мечі виявились різної маси. Коваль вирішив, що найважчий меч отримає найсильніший із рицарів. Майстру вдалось не більш ніж за 5 зважувань розмістити мечі за зростанням маси. Спробуйте зробити це і ви.

Підказка. Пронумеруйте мечі: 1, 2, 3 і 4. Порівняйте мечі 1 і 2; 3 і 4 (два зважування). Потім порівняйте між собою більш важчі і більш легші мечі.

Задача 4. Король вирішив подарувати своєму сину земельні угіддя і побудувати там замок. Майстри сказали, що для цього їм знадобиться 9 кг цвяхів. В коморах замку знайшли мішок з цвяхами масою 24 кг. Як відміряти 9 кг цвяхів?

Розв’язання.

Розділимо цвяхи на дві кучки та, щоб при зважуванні ваги виявились у рівновазі. В кожній купці цвяхів буде по _______________ кг.
Одну із купок знову поділимо навпіл. Отримаємо дві купки по ___________ кг.
Одну із купок ділимо навпіл. Отримуємо дві купки по ______________ кг.
Складаємо 9 кг цвяхів із купок по _________ кг і ____________ кг.

Домашнє завдання

На столі в ряд лежать 4 монети. Серед них є як справжні, так і фальшиві (вони легші від справжніх). Відомо, що будь-яка справжня монета знаходиться лівіше від фальшивої. Як за одне зважування виявити монету?

Урок №11

Турнір – задачі на переливання і зважування

Інтелектуальна розминка

Переставте букви у слові «клоун» так, щоб отримати два нових слова.

Веселі задачки

На листок із записами прикладу впали краплинки, закривши знаки «+» і «-». Здогадайтесь, які знаки потрібно поставити замість краплинок так, щоб рівність була правильною:

Переставте числа в квадраті так, щоб сума чисел по всім горизонталям, вертикалям і діагоналям була однаковою.

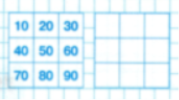
Старовинні задачки.

Задача Діофанта. Знайдіть три числа, якщо відомо, що добуток суми перших двох чисел і третього числа дорівнює 35, добуток суми першого і третього чисел на друге – 27, а добуток смуи другого і третього на перше – 32.

Підказка.

Задача про школу Піфагора. Тиран острава Самос Полікрат одного разу на балу запитав у Піфагора, скільки у нього учнів. «Із задоволенням скажу тобі, о Полікрат!» - відповів вчитель. «Половина моїх учнів вивчає прекрасну математику, чверть вивчає таємниці вічної природи, сьома частина тренує силу духу, зберігаючи в серці навчання. Додай до них ще трьох юнаків, із яких Теон найкращий. Скільки учнів я навчаю?» Тож скільки учнів було у Піфагора?

Числові головоломки

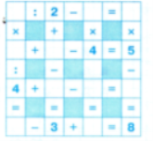Проведіть ламану лінію від цифри 1 у верхньому лівому кутку в нижній правий куток з цифрою 9 так, щоб сума всіх чисел, перекреслених цією лінією, дорівнювала 100. Рухатись можна лише вправо і вниз.

Заповніть арифметичний коврик числами.

Розповідають, що два батька і два сина знайшли на дорозі, яка веде до Бомбею, три рупії (срібні монети) і швидко розділили їх між собою, причому кожному дісталось по монеті. Як їм вдалось справитись з цією задачею?
Геометричні фігури вирішили помінятись своєю роллю з цифрами. Відновіть запис з урахуванням того, що однакові фігури відповідають однаковим цифрам.

Звірі вирішили перевірити, хто важчий – носоріг чи бегемот. Вони запросили мавпочку – і та згодилась керувати процесом зважування. В результаті виявилось, що 3 носороги важать стільки, скільки 4 бегемоти і один крокодил. А от зрозуміти, хто ж важчий, їм так і не вдалось. Допоможіть звірям!
Розставте замість зірочок математичні знаки так, щоб після послідовного виконання дій отримати задані результати.

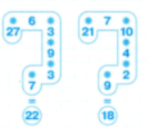
В прикладі на множення частину цифр замінили зірочками. З’ясуйте, яких цифр н вистачає, щоб приклад був розв’язаний правильно.

Відмітьте задачі, які вам вдалось розв’язати (номер задачі обведіть кружечком).

Номер задачі	1	2	3	4	5	6	7	8	9	10	11	12
Оцінка

Тема №5. Дидактичні ігри

Уроки №1, 2

Математичні фокуси

Фокус з календарем

Вражати друзів за допомогою знань деяких математичних закономірностей дуже просто. Та ще й неабияк цікаво!

Скажіть присутнім, що легко зможете вирахувати суму дев’яти будь-яких чисел, які друзі загадають, не знаючи, що це за числа.

Для цього нехай хтось один відмітить на календарі дев’ять чисел так, щоб вони утворили квадрат, а вам лише назве найменше число із відмічених. І ви одразу, або ж трішки подумавши, назвете суму.

Секрет такий: для цього до названого числа додайте 8, а результат помножте на 9. Наприклад, закреслено так, як показано на малюнку. Отож, найменшою є цифра 3.

Далі робимо таким чином: 3 + 8 = 11, 11 х 9 = 99. Оголошуємо суму – 99. Ну, тепер нехай друзі додають і перевіряють результат.

Звісно, спочатку необхідно навчитися гарно і швидко рахувати в умі.

Отож вперед вчити математику!

Таємниця дати народження

Для цього математичного фокусу Тобі потрібно знати дату народження (день і місяць) свою, або будь-кого іншого, а також калькулятор чи папір і ручка, щоб зробити правильні підрахунки.

Ну що, готовий до несподіванки? Тоді вперед!

Перший крок: день народження помножити на 2 (два);

Другий крок: до отриманого результату додати 5 (п’ять);

Третій крок: отримане число помножити на 50 (п’ятдесят);

Четвертий крок: додати номер місяця, в якому народився;

П’ятий крок: від отриманої суми віднімаємо 250 (двісті п’ятдесят);

Результатом має бути три або чотири цифри. Їх значення Ти, напевно, зрозумієш сам.))

Загадки чисел

Цю гру можна назвати також дослідом. Виконуючи кожну дію, будь уважним. Дотримуйся поданих вказівок.

І так, для початку Тобі потрібен калькулятор, або ж відкрий його на комп’ютері, і Твій номер телефону.

Тепер уважно читай завдання і ретельно виконуй кожну дію.

1. Для початку згадай або подивись три перші цифри свого номеру телефону. Зверни увагу, код оператора чи міста не враховується!

2. Множимо ці цифри на 80.

3. Наступний крок – це додавання до отриманого числа 1.

4. Число, отримане в результаті, множимо на 250.

5. Тепер згадай 4 останні цифри свого номеру телефону і додай їх.

6. Дію повторюємо знову, тобто ще раз додаємо 4 останні цифри Твого номеру телефону.

7. А зараз віднімаємо 250.

8. Отримане число ділимо на 2.

Математичне чаклунство

Багато хто вважає математику нудною і важкою наукою: складні задачки, рівняння, формули… Голова обертом. Проте світ чисел і прикладів набагато цікавіший, ніж здається на перший погляд. Хочеш відчути себе фокусником і викликати захоплення та здивування у друзів? Тоді вперед!

За допомогою цього фокусу Ти зможеш безпомилково порахувати, скільки братів і сестер у Твоїх знайомих, не питаючи їх про це. Необхідно, щоб спочатку Твій друг (чи подружка) до кількості своїх братів додав число 3 (але тобі результат поки не каже).

Потім отримане число помножить на 5, приплюсує 20, суму помножить на 2.

До результату необхідно додати ще й кількість сестер, плюс число 5.

Він чи вона називають остаточний результат. Тоді справа за Тобою!

Від отриманого числа відніми 75 (звісно, другу про це нічого не кажи). Двозначне число, яке Ти отримаєш, вкаже на склад сім'ї: перша цифра – кількість братів, друга – сестер.

Ось як усе просто!

Домашнє завдання.

Знайти один математичний фокус і запропонувати його однокласникам.