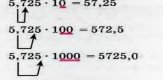Посібник для уроків математики 5 класу ІІ семестру (оновлений)
Ківерцівська експериментальна школа
Навчальний посібник


___________________________________
___________________________________
Шановний п’ятикласнику!
Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. У цьому тобі допоможе навчальний посібник, який ти тримаєш в руках.
Посібник складається з чотирьох тем. Кожна тема має таку структуру:
- перший урок – урок розбору блоку навчальної інформації;
- наступні уроки – уроки фронтального опрацювання матеріалу, на яких ти зможеш засвоїти поняття, терміни і правила блоку навчальної інформації, також навчитись застосовувати ці знання для розв’язування різноманітних задач і вправ.
-
між уроками фронтального опрацювання ти будеш виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені

- в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.
Також в кінці посібника є блок №11 – повторення всього матеріалу, вивченого у 5 класі, під час вивчення якого ти зможеш узагальнити все, про що дізнався на уроках математики протягом року.
Нехай Бог посилає тобі мудрості у вивченні математики!!!
Тема №7. Звичайні дроби та дії над ними
Урок №1

Звичайні дроби та дії над ними
«Хто з мудрими ходить, той мудрим
стає, а хто товаришує з безумним, той лиха набуде»
Книга Приповістей Соломонових 13:20
Питання
- Звичайні дроби.
- Звичайні дроби і ділення натуральних чисел.
- Порівняння звичайних дробів з однаковими знаменниками.
- Правильні і неправильні дроби.
- Мішані числа.
- Додавання і віднімання дробів з однаковими знаменниками. Додавання і віднімання мішаних чисел.
Література
Істер О.С. Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – §§27 – 33, ст. 157 – 193.
|
1. Звичайні дроби |
||
|
1.1 |
Коли один предмет або одиницю виміру ділять на рівні частини, виникають дробові числа. Звичайні дроби записуються за допомогою двох натуральних чисел і горизонтальної риски.
|
Півхлібини,
|
|
1.2 |
Число, записане над рискою, називають чисельником дробу, число, записане під рискою – знаменником дробу.
|
|
|
2. Звичайні дроби і ділення натуральних чисел |
||
|
2.3 |
Значення дробу дорівнює частці від ділення чисельника дробу на його знаменник. |
|
|
2.4 |
Частка від ділення одного числа на інше дорівнює дробу, чисельник якого дорівнює діленому, а знаменник – дільнику. |
|
|
3. Порівняння звичайних дробів з однаковими знаменниками |
||
|
3.5 |
Із двох дробів з однаковими знаменниками той дріб більший, чисельник якого більший, і той дріб менший, чисельник якого менший.
|
|
|
3.6 |
Більшому дробу на координатному промені відповідає точка, що лежить правіше, а меншому – точка, що лежить лівіше.
|
|
|
3.7 |
З двох дробів з однаковими чисельниками більшим є той, знаменник якого менший, а меншим є той знаменник якого більший. |
|
|
4. Правильні і неправильні дроби |
||
|
4.8 |
Дріб, чисельник якого менший від знаменника, називається правильним. |
|
|
4.9 |
Дріб, чисельник якого більший від знаменника або дорівнює йому, називається неправильним. |
|
|
4.10 |
Правильний дріб менший від 1. |
|
|
4.11 |
Якщо чисельник і знаменник неправильного дробу рівні між собою, то такий дріб дорівнює 1. |
|
|
4.12 |
Якщо чисельник неправильного дробу більший за знаменник, то цей дріб більший за 1. |
|
|
5. Мішані числа |
||
|
5.13 |
Число, яке є сумою натурального числа (ціла частина) і звичайного дробу (дробова частина), називають мішаним числом. |
|
|
5.14 |
Щоб неправильний дріб перетворити у мішане число, треба чисельник поділити на знаменник. Отримана неповна частка буде цілою частиною мішаного числа, а остача – чисельником дробової частини.
|
|
|
5.15 |
Щоб мішане число перетворити в неправильний дріб, треба цілу частину помножити на знаменник дробової частини і до отриманого добутку додати чисельник дробової частини. Ця сума є чисельником неправильного дробу, а його знаменник дорівнює знаменнику дробової частини мішаного числа. |
|
|
6. Додавання і віднімання дробів з однаковими знаменниками. Додавання і віднімання мішаних чисел. |
||
|
6.16 |
Щоб додати дроби з однаковими знаменниками, треба їхні чисельники додати і залишити той самий знаменник. |
|
|
6.17 |
Щоб відняти дроби з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від’ємника і залишити той самий знаменник. |
|
|
6.18 |
При додаванні мішаних чисел цілі частини додаються окремо, дробові частини – окремо. |
|
|
6.19 |
При відніманні мішаних чисел, коли дробова частина зменшуваного більша за дробову частину від’ємника доцільно цілі частини відняти окремо, а дробові — окремо та додати отримані числа. |
|
Уроки №2, 3
«Без знання дробів ніхто
не може визнавати, що знає математику»
Цицерон, давньоримський політичний діяч
Фронтальне опрацювання матеріалу
Звичайні дроби
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.4 блоку № 7.
- Усно дай відповідь на питання:
- Коли виникають дробові числа?
- З чого складається дріб?
- Число, що записується під рискою звичайного дробу, називається …
- Число, що записується над рискою звичайного дробу, називається …
- Риска дробу означає дію …
- Що показує знаменник дробу?
-
Що показує чисельник дробу?
- Перегляньте інформацію:
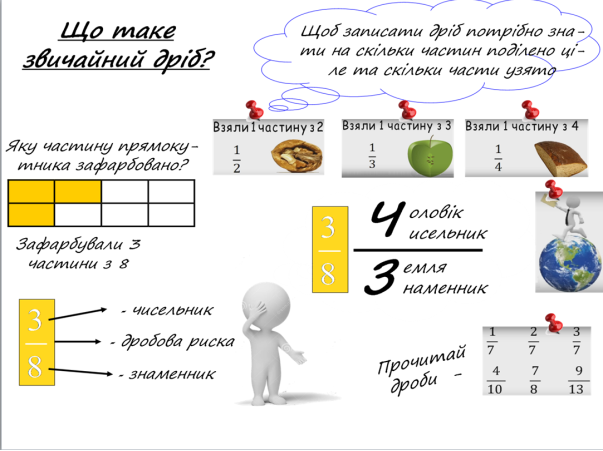
Завдання 2.
- Яка частина фігури зафарбована?


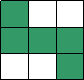

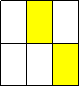
- Усно виконай вправи, стор. 159 підручника: 918, 919.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Розглянь приклади 1 – 3 на сторінці 158 підручника.
- Користуючись розглянутими прикладами, письмово виконай вправи, стор. 160 підручника: 921, 923, 931, 942.
Завдання 4.
- Розглянь задачу 1 на сторінці 158 підручника. Сформулюй правило знаходження дробу від числа.
- Користуючись розглянутим прикладом і сформульованим правилом, письмово виконай вправи, стор. 161 підручника: 938, 946, 948, 950.
Завдання 5.
- Розглянь задачу 2 на сторінці 159 підручника. Сформулюй правило знаходження числа за значенням його дробу.
- Користуючись розглянутим прикладом та сформульованим правилом, письмово виконай вправи, стор. 209 – 210 підручника: 951, 953, 955.
Урок №4
«Не кажи чому учився, а що пізнав»
Народна мудрість
Фронтальне опрацювання матеріалу
Звичайні дроби і ділення натуральних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.4 блоку № 7.
- Усно дай відповідь на питання:
- Коли виникають дробові числа?
- Як записують звичайні дроби?
- Що називають чисельником і знаменником дробу?
- Що показує знаменник дробу?
- Що показує чисельник дробу?
- Що означає риска дробу?
- Чому дорівнює значення дробу?
- Чому дорівнює частка від ділення одного числа на інше?
Завдання 2.
 Усно розв’яжи вправи:
Усно розв’яжи вправи:
- Пиріг розрізали на 8 рівних шматків.
- Яку частину пирога становить 1 шматок?
- Яку частину пирога становлять 3 шматки?
- Яку частину пирога становлять усі шматки?
- Розділити порівну 6 плиток шоколаду між трьома дітьми.
- Розділити порівну 3 плитки шоколаду між трьома дітьми.
- Розділити порівну 2 плитки шоколаду між трьома дітьми.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправу, стор. 166 підручника: 966.
Завдання 4.
Заповни порожні місця в таблиці:
|
Частка |
Дріб |
Ділене |
Дільник |
Чисельник |
Знаменник |
|
5 : 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
14 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
11 |
Завдання 5.
Письмово виконай вправи, стор. 166 підручника: 967, 968 (самостійно), 971, 973, 974 (самостійно), 975.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 6.
Ненажерки Хрум, Трям і Ням вирішили на свято спекти пироги. Хрум випік 2 пироги, і Трям 2, а Ням зміг спекти тільки 1 пиріг. Як їм поділити порівну 5 пирогів на трьох? Яку частину від усіх пирогів отримає кожен?
Уроки №5, 6
«Бога повинно слухатись більш, як людей!»
Дії святих апостолів 5:29
Фронтальне опрацювання матеріалу
Порівняння звичайних дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.7 блоку №7.
- Дай відповіді на питання:
- Коли виникають дробові числа?
- Як порівняти два дроби з однаковими знаменниками?
- Як порівняти два дроби з однаковими чисельниками?
- Як порівняти звичайні дроби за допомогою координатного променя?
- З чого складаються звичайні дроби?
- Що показують чисельник і знаменник звичайного дробу?
Завдання 2.
Усно розв’яжи вправи:
-
 Ведмідь сперечається з вовком: у кого важчий мішок. Ведмідь каже, що у нього мішок заповнений на
Ведмідь сперечається з вовком: у кого важчий мішок. Ведмідь каже, що у нього мішок заповнений на 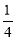 , а у вовка на
, а у вовка на 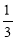 , і оскільки 4 > 3, то у нього мішок важчий. Допоможіть їм розв’язати цю проблему.
, і оскільки 4 > 3, то у нього мішок важчий. Допоможіть їм розв’язати цю проблему.

-
Старенька Сова задумала полетіти до своєї доньки – Совички. Вона пролетіла
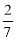 частини шляху без відпочинку. Їй залишилось пролетіти ще
частини шляху без відпочинку. Їй залишилось пролетіти ще 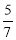 . Допоможіть старенькій з’ясувати: вона пролетіла більшу чи меншу частину шляху?
. Допоможіть старенькій з’ясувати: вона пролетіла більшу чи меншу частину шляху?

-
Зайченятка на велосипедах виїхали з різних кінців лісу назустріч один одному. Перший зайчик проїхав
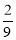 км всього шляху, а другий -
км всього шляху, а другий -  км. Хто із зайців проїхав більшу відстань?
км. Хто із зайців проїхав більшу відстань?
-
 Білочка порахувала свої запаси на зиму і з’ясувала, що вже
Білочка порахувала свої запаси на зиму і з’ясувала, що вже 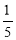 частину сушених грибів і
частину сушених грибів і  частину горішків вона з’їла. Яких запасів білочка з’їла більше: сушених грибів чи горіхів?
частину горішків вона з’їла. Яких запасів білочка з’їла більше: сушених грибів чи горіхів?
Завдання 3.
Усно виконай вправи, стор. 169 підручника: 981, 982, 983.
ІІ. Відпрацювання умінь і навичок розв’язування задач
Завдання 4.
Письмово виконай вправи, стор. 169: 985, 986, 991, 993, 996, 997.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 5.
- Чи правильно виконано порівняння? Виправити помилку. Відповідь пояснити.
![]() <
<![]() ,
, ![]() <
<![]() ,
, ![]() >
>![]() ,
, ![]() >
>![]() .
.
- Записати по два числа замість зірочки, щоб утворилась правильна нерівність:
![]() <
<![]() ,
, ![]() >
> ![]() ,
, ![]() <
< ![]() ,
, ![]() >
>![]()
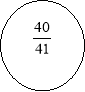
- В порожніх колах поставити знаки « = », « < », « >».




![]()

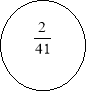


![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
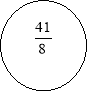
![]()

![]()

![]()
![]()
Урок №7
Щоб наш урок був плідним, будемо:
не просто слухати, а чути;
не просто дивитися, а бачити;
не просто відповідати, а міркувати;
дружно й плідно працювати!
Індивідуальне опрацювання матеріалу
Порівняння звичайних дробів
Виконання практичної роботи «Тема 7 робочий зошит «Я дослідник»
Урок №8
«Наблизьтесь до Бога, то й Він наблизиться до вас…»
Послання апостола Якова 4:8
Фронтальне опрацювання матеріалу
Правильні і неправильні дроби
І. Робота над засвоєнням понять термінів і правил
Завдання 1.
- Повтори тези 1.1 – 4.12 блоку №7.
- Дай відповіді на питання:
- Число записане над рискою дробу, називається…
- Число записане під рискою дробу, називається…
- Чисельник вказує на …
- Знаменник вказує на …
- Риску дробу можна замінити …
- Дроби бувають …
- Правильний дріб – це …
- Неправильний дріб – це …
- З чого складаються звичайні дроби?
- Коли виникають дробові числа?
- Сформулюй правила порівняння дробів з одиницею.
Завдання 2.
![]()
- Чому деякі дроби записані одним кольором, а деякі — іншим?
- Що спільного у всіх дробів, записаних синім кольором?
- Що спільного у всіх дробів, записаних червоним кольором?
Завдання 3.
Виконай усно вправу, стор. 172 підручника: 1000.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Виконай письмово вправи, стор. 172 підручника: 1002, 1008 (1, 3, 5, 7, 9), 1010, 1011, 1017, 1019, 1026.
Завдання 5.
Накресли координатний промінь і візьміть за одиничний відрізок 12 клітинок. Відміть точки: О(0); E(1); А(2); К![]() ; М
; М![]() ; N
; N![]() ; Р
; Р![]() ; S
; S![]() ; Т
; Т ![]() ; С
; С![]() .
.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Запишіть у вигляді дробів 1, 2, 6, 12, 30 частин числа, яке поділили на 60 частин.
-
Накресліть координатний промінь. Виберіть зручний одиничний відрізок і позначте на промені такі точки:
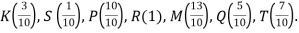
-
У крамниці за три дні було продано 36 коробок цукерок. У п’ятницю було продано
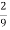 усіх коробок, у суботу
усіх коробок, у суботу 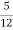 , а решту – у неділю. Скільки коробок цукерок було продано у неділю?
, а решту – у неділю. Скільки коробок цукерок було продано у неділю?
-
У 5-А класі навчається німецьку мову вивчають 10 учнів, що складає
 усієї кількості учнів у класі. Скільки учнів у 5-А класі?
усієї кількості учнів у класі. Скільки учнів у 5-А класі?
Уроки №10, 11
«Я можу все в Тім, Хто мене підкріпляє, – в Ісусі Христі »
Послання апостола Павла до филипʼян 4:13
Фронтальне опрацювання матеріалу
Мішані числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 5.15 блоку № 7.
- Дай відповіді на питання:
- Коли один предмет або одиницю виміру ділять на рівні частини, отримують…
- Число записане над рискою дробу, називають…
- Число, що показує на скільки рівних частин поділили щось ціле, називається …
- Дріб, у якого чисельник менший від знаменника, називається…
- Риску дробу можна розглядати як знак…
- Що називають мішаним числом?
- Як перетворити неправильний дріб у мішане число?
-
Як мішане число перетворити у неправильний дріб?
- Запам’ятай правило перетворення мішаного числа в неправильний дріб і неправильного дробу у мішане число:
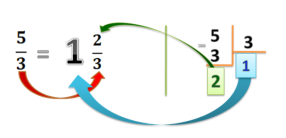
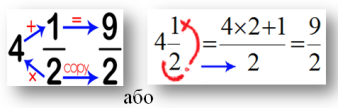
Завдання 2.
- Виконай усно вправу 1032, стор. 177 підручника.
- Прочитай останній абзац §31, стор. 177. Коли про число кажуть, що воно не має дробової частини? Коли про число кажуть, що воно немає цілої частини?
- Користуючись отриманими у завданні 2.2 висновками, усно виконай вправи 1037, 1038, стор.177, 178 підручника.
ІІ. Відпрацювання умінь і навичок розв’язування вправ
Завдання 3.
- Письмово виконай вправи, стор. 177: 1033; 1035.
- Розглянь приклад 1, стор.176 підручника. Користуючись розглянутим прикладом, виконай письмово вправи, стор.178, 1039; 1041.
Завдання 4.
Виконай письмово вправи, стор.178 – 179 підручника: 1045, 1047, 1049, 1054, 1055, 1058.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 5.
Замість квадратиків запиши такі числа, щоб утворились правильні рівності:
1) ![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Уроки №12, 13
«Любов виникає з любові; коли хочу,
щоб мене любили, я сам перший люблю»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Додавання і віднімання звичайних дробів з однаковими знаменниками
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок №7.
- Дай відповіді на питання:
- Які дроби називаються правильними?
- Як перетворити мішане число в неправильний дріб?
- Які дроби називаються неправильними?
- Дайте визначення мішаному числу.
- З чого складаються звичайні дроби?
- Як додати дроби з однаковими знаменниками?
- Як порівняти дроби з однаковими знаменниками?
- Як відняти дроби з однаковими знаменниками?
- Як порівнювати звичайні дроби з одиницею?
Завдання 2.
Усно виконай вправи, запропоновані вчителем (презентація).
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Письмово виконай вправи, стор. 182 підручника: 1066, 1068, 1070, 1074, 1079, 1082, 1086.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
Письмово виконай вправи, стор. 237 – 238: 1087, 1089, 1090.
Уроки №14, 15
«З усіх утрат втрата часу найтяжча»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Додавання і віднімання мішаних чисел
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку №7.
- Дай відповіді на питання:
- Коли виникають дробові числа?
- Як мішане число перетворити у неправильний дріб?
- Як додати мішані числа?
- Що називають мішаним числом?
- З чого складаються звичайні дроби?
- На що вказують знаменник і чисельник дробу?
- Як порівняти звичайні дроби з однаковими знаменниками?
- Як перетворити неправильний дріб у мішане число?
- Як додати два дроби з однаковими знаменниками?
- Як порівняти два дроби з однаковими чисельниками?
Завдання 2.
Усно виконай вправу:
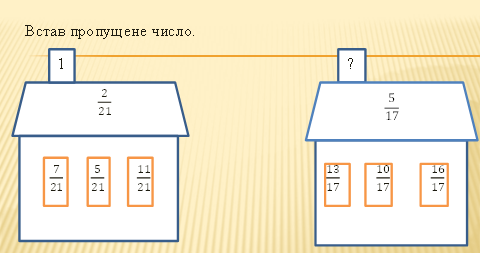
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Розглянь приклади 1, 2, 3, стор. 186 підручника.
- Користуючись розглянутими прикладами, виконай вправи, стор. 187 підручника: 1098, 1099.
Завдання 4.
- Розглянь приклади 4, 5, стор. 187 підручника. Дай відповідь на питання:
- Як від цілого числа відняти правильний дріб?
-
Як відняти мішані числа, у яких дробова частина зменшуваного менша за дробову частину від’ємника?
- Користуючись розглянутими прикладами та зробленими висновками, виконай письмово вправи, стор. 188 підручника: 1101, 1103, 1105, 1109, 1112.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 5.
- Знайдіть невідомі числа в ланцюжку обчислень:
-
Скільки потрібно змолоти пшениці, щоб одержати 32 ц борошна, якщо маса борошна становить
 маси пшениці?
маси пшениці?
Завдання 6.
Виконати завдання практичної роботи, запропонованої вчителем.
- Розмалюй частини, щоб проілюструвати дроби.
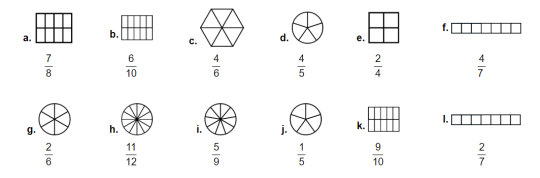
- Запиши дріб, який відповідає зафарбованій частині.
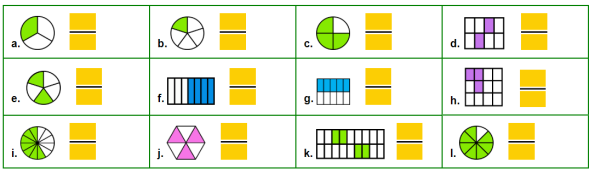
- Запиши дріб, який відповідає зафарбованій частині.
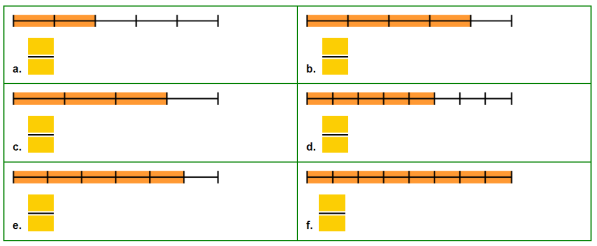
- Застосуй інформацію про поділ круга на частинки і поділи круги і зафарбуй частини, щоб проілюструвати дроби.
|
Половинки: поділи круг навпіл прямою лінією.
|
Третина: поділи круг, намалювавши лінії на 12, 4, 8 годин.
|
|
Четвертина: спочатку намалюйте половинки, а потім поділіть їх навпіл.
|
П’ять частин: малювати як людину, яка розкинула руки і ноги.
|
|
Шість частин: спочатку поділити на третини, а потім кожну розділити навпіл.
|
Вісім частин: спочатку намалюй четвертини, а потім розділи їх навпіл.
|
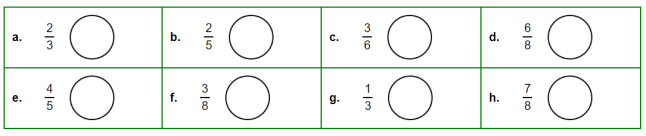
- Все ціле = 1. Запиши 1 як дріб, користуючись прикладом.

- Поділи фігури на рівні частини і зафарбуй деякі елементи, щоб проілюструвати дроби.
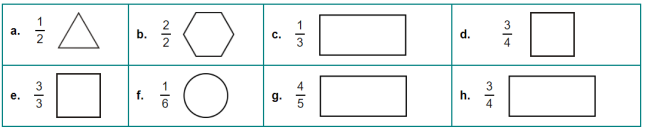
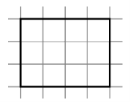
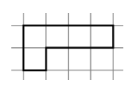
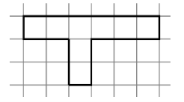
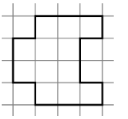
- Поділіть фігуру на рівні частини. Все, що виділено чорною лінією, дорівнює 1. Запишіть площу частинки як частину всієї фігури за допомогою звичайного дробу.
|
Розділіть фігуру на дві рівні частини
1 частинка = |
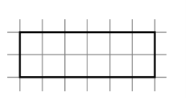
Розділіть фігуру на три рівні частини
1 частинка = |
|
Розділіть фігуру на шість рівних частин
1 частинка = |
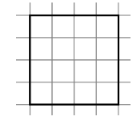
Розділіть фігуру на чотири рівні частини
1 частинка = |
|
Розділіть фігуру на три рівні частини
1 частинка = |
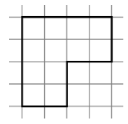
Розділіть фігуру на п’ять рівних частин
1 частинка = |
|
Розділіть фігуру на чотири рівні частини
1 частинка = |
Розділіть фігуру на чотири рівні частини
1 частинка = |
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Обчислити: 1)
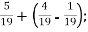 2)
2)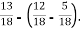
-
На базу завезли яблука на двох вантажних машинах. На першій було
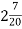 т, на другій -
т, на другій - 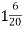 т яблук. На скільки більше яблук на першій машині, ніж на другій?
т яблук. На скільки більше яблук на першій машині, ніж на другій?
-
Обчислити:
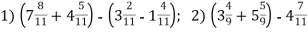 .
.
-
Швидкість катера
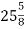 км/год. Швидкість течії річки
км/год. Швидкість течії річки 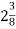 км/год. Знайдіть швидкість катера за течією і проти течії річки.
км/год. Знайдіть швидкість катера за течією і проти течії річки.
-
Розв'язати рівняння:
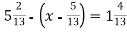 .
.
-
Учень прочитав 120 сторінок, що становить
 книжки. Скільки сторінок залишилось прочитати учню?
книжки. Скільки сторінок залишилось прочитати учню?
Урок №17
«Тим, хто не знає математики, важко
збагнути справжню, глибоку красу природи»
Річард Фейнман, американський фізик
Внутрішньопредметне узагальнення матеріалу
Звичайні дроби та дії над ними
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 7.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
- Записати дріб, який утвориться, коли щось ціле поділити на 8 частин і взяти 5 частин.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скільки серед дробів
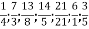 є неправильних?
є неправильних?
|
А |
Б |
В |
Г |
|
2 |
3 |
4 |
5 |
-
Вкажіть натуральне число, яке дорівнює значенню неправильного дробу
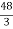 .
.
|
А |
Б |
В |
Г |
|
19 |
16 |
17 |
18 |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
-
Обчислити: 1)
 ; 2)
; 2) 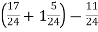 .
.
-
У книжці Івана Крип’якевича «Історія України» 168 сторінок. Галя прочитала
 книжки. Скільки сторінок прочитала Галя?
книжки. Скільки сторінок прочитала Галя?
-
З винограду отримали 18 кг родзинок, що становить
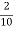 маси винограду. Скільки було взято винограду?
маси винограду. Скільки було взято винограду?
-
Розв’яжіть рівняння: 1)
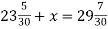 ; 2)
; 2) 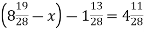 .
.
-
У книжці 60 сторінок. Михайлик прочитав
 усієї книги. Скільки сторінок залишилося прочитати?
усієї книги. Скільки сторінок залишилося прочитати?
-
Катеру потрібно пропливти 92 км. За першу годину він проплив
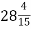 км, за другу –
км, за другу – 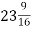 км, за третю –
км, за третю – 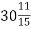 км. Скільки кілометрів залишилося пропливти катеру?
км. Скільки кілометрів залишилося пропливти катеру?
Тема №8. Десяткові дроби. Додавання і віднімання десяткових дробів
Урок №1

Десяткові дроби. Додавання та віднімання десяткових дробів
«Глядіть, щоб ніхто
нікому не віддавав злом за зло, але завжди
дбайте про добро один для одного й для всіх!»
1послання ап. Павла до солунян 5:15
Питання
- Десятковий дріб, запис десяткових дробів
- Порівняння десяткових дробів
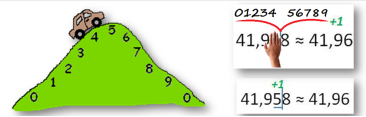
- Округлення натуральних чисел і десяткових дробів
- Додавання і віднімання десяткових дробів
Література
Істер О.С. Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – §§34 – 37, ст. 193 – 220.
|
|||||||||||||||||||||||||||||||
|
1.1 |
Дроби, в яких знаменники є числами 10, 100, 1000 і т. д. називають десятковими. В записі десяткового дробу ціла і дробова частини відокремлюються комою. |
|
|||||||||||||||||||||||||||||
|
1.2 |
Запис дробової частини містить стільки цифр, скільки нулів у запису знаменника відповідного звичайного дробу. |
|
|||||||||||||||||||||||||||||
|
1.3
|
Розряди дробової частини десяткового дробу: розряд десятих, розряд сотих, розряд тисячних, розряд десятитисячних і т. д.
|
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
2.4 |
Якщо справа до десяткового дробу приписати один чи кілька нулів або відкинути один чи кілька нулів, то отримаємо дріб, що дорівнює даному. |
|
|||||||||||||||||||||||||||||
|
2.5 |
Із двох десяткових дробів більший той, у якого більша ціла частина; якщо десяткові дроби мають рівні цілі частини, то більшим буде той дріб, в якого більше число десятих; якщо число десятих однакове, то більшим буде дріб, у якого більше число сотих і т.д.
|
11,25 > 6,32 135,2 < 200,45 12,35 > 12,14
14,43 14,2 = 14,20 |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
3.6 |
Округлення натуральних чисел: 1) округлюючи натуральне число до певного розряду всі цифри, що йдуть за ним, замінюють нулями; 2) якщо перша наступна за цим розрядом цифра 5, 6, 7, 8, 9, то останню цифру, яка залишилась збільшують на одиницю; 3) Якщо перша наступна за цим розрядом цифра 0, 1, 2, 3, 4, то останню цифру, яка залишилась, не змінюють. |
Округли 435 до десятків
435 |
|||||||||||||||||||||||||||||
|
3.7 |
Округлення десяткових дробів: 1) округлюючи десятковий дріб до певного розряду, усі цифри, записані за цим розрядом, замінюємо нулями або відкидаємо (якщо вони стоять після коми); 2) якщо першою цифрою за цим розрядом є 0, 1, 2, 3 або 4, то останню цифру, що залишилася, не змінюємо; 3) якщо першою цифрою за цим розрядом є 5, 6, 7, 8 або 9, то останню цифру, що залишилася, збільшуємо на 1.
|
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
4.8 |
Щоб додати (відняти) десяткові дроби, потрібно їх записати один під другим так, щоб кома стояла під комою, виконати додавання (віднімання) і в результаті кому поставити під комою. Якщо в дробах різна кількість цифр після коми, то її потрібно зрівняти, приписуючи справа нулі. |
|
|||||||||||||||||||||||||||||
|
4.9 |
Властивості додавання Переставна Від перестановки доданків сума не змінюється. Сполучна Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього. |
|
|||||||||||||||||||||||||||||
Уроки №2, 3
«Що вподобав, на те й перетворився»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Десяткові дроби. Читання і запис десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку №8.
- Усно дай відповіді на питання:
- Які дроби називаються десятковими?
- Як у десяткових дробах відокремлюються ціла та дробова частини?
- Скільки цифр містить запис дробової частини десяткового дробу?
- Назви розряди дробової частини десяткового дробу.
Завдання 2.
- Прочитай числа:
1) 0,2; 2) 18,001; 3) 7,0101;
5,7; 0,0004; 29,00601;
16,4; 46,0732; 387,100056;
0,27; 1238,0072; 0,0000101;
4,31; 35,0000063; 5,00001004.
- Заміни знак питання такими цифрами, щоб одержати правильну рівність:
1) ![]() = 0,23 ; 2)
= 0,23 ; 2) ![]() = 0,452 ; 3)
= 0,452 ; 3) ![]() = 0,? ;
= 0,? ;
4) ![]() = 0,? ; 5)
= 0,? ; 5) ![]() = 0,045 ; 6)
= 0,045 ; 6)![]() = 0,00475 .
= 0,00475 .
- Усно виконай завдання, запропоновані вчителем (презентація).
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Усно виконай вправи, стор. 195 підручника: 1127; 1128.
- Письмово виконай вправи, стор. 196 підручника: 1129 (1, 3, 5, 7, 9, 11); 1131; 1133 (1, 3, 5); 1136 (2, 4, 6); 1137 (1, 3, 5); 1139 (2, 4, 6);
- Письмово виконай вправи, стор. 197 підручника:1142; 1149; 1151 (1, 3, 5); 1159; 1155.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
 Завдання 4.
Завдання 4.
Виконай вправу:
Івасик придумав на урок чотири рівності з десятковими і звичайними дробами. Ліві і праві частини цих рівностей він написав на окремих картках. Прийшовши до школи він забув, які з цих дробів рівні. Допоможіть Василькові встановити відповідність між цими дробами.
1 – 0, 24 А – ![]()
2 – 3,76 Б – ![]()
3 – 3,076 В – ![]()
4 – 0,024 Г – ![]()
Уроки №4, 5
«Хіба не любов усе єднає, будує,
творить, подібно до того, як ворожість руйнує?»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Порівняння десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.5 блоку № 8.
- Дай відповідь на питання:
- Які дроби називаються десятковими?
- Як у десяткових дробах відокремлюються ціла та дробова частини?
- Скільки цифр містить запис дробової частини десяткового дробу?
- Назви розряди дробової частини десяткового дробу.
- Коли отримаємо дріб рівний даному десятковому дробові?
-
Сформулюй правило порівняння десяткових дробів.
- Відшукай помилку:
![]()
- Розглянь приклади порівняння десяткових дробів, запропоновані вчителем (презентація).
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
- Виконай усно вправи, стор. 202 підручника: 1173, 1175.
- Виконай письмово вправи, стор. 203 підручника: 1177, 1179.
- Виконай письмово вправи, стор. 203 підручника: 1182, 1183.
- Виконай письмово вправи, стор. 203 підручника: 1187, 1188.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 3.
Виконати самостійно завдання практичної роботи
Практична робота
Порівняння десяткових дробів
Підказка!!!
Десяткові дроби легко порівнювати за допомогою таких таблиць:
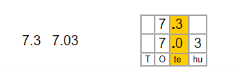
Для цього числа записують одне під іншим так, щоб кома була під комою. І після цього порівнюють числа за правилом порівняння десяткових дробів.
-
 Виконайте наступні завдання:
Виконайте наступні завдання:
- Що більше 0,3 чи 0,21?
- Намалюйте координатний промінь від 0,5 до 0,6 і розмістіть на ній числа 0,55 і 0,6. Для прикладу використайте координатний промінь попереднього завдання. Що більше 0,55 чи 0,6?
- Розташуйте числа 5,2 і 5,02 на даному координатному промені.

- Розташуйте числа у порядку зростання. Пам’ятайте, що числа легше порівнювати, якщо вони мають однакову кількість знаків після коми. Ви також можете використовувати координатний промінь з попереднього завдання.
![]()
-
Порівняйте і напишіть знаки
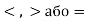 . Використовуйте таблички, якщо це вам необхідно.
. Використовуйте таблички, якщо це вам необхідно.

4. Порівняйте
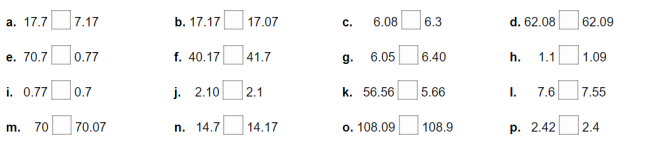
- Обведіть найбільше число

- Розташуйте числа від найменшого до найбільшого
![]()
![]()
- Наведіть приклад двох десяткових дробів, у яких:
- Число, з більшою кількістю цифр менше від іншого;
- Число з більшою кількістю цифр більше від іншого;
- Число, з більшою кількістю цифр дорівнює іншому.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Запиши усі цифри, які можна поставити замість зірочки, щоб нерівність
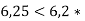 була правильною.
була правильною.
- Розташуй числа у порядку зростання: 5,47; 3,002; 5,55; 5,555; 3,02.
-
Які натуральні числа можна поставити замість
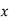 , щоб нерівність була правильною:
, щоб нерівність була правильною: 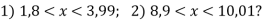
- Накресли координатний промінь. За одиничний відрізок візьми 10 клітинок зошита. Познач на промені числа: 0,4; 0,5; 0,7; 1,3; 1,5; 1,8.
- Порівняй величини: 1) 4,17 дм і 41,8 см; 2) 0,42 м ² і 4,2 дм ².
-
Запиши три числа, які можна поставити замість
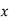 , щоб була правильною нерівність:
, щоб була правильною нерівність: 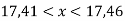 .
.
Уроки №7, 8
«Хто думає про науку, той любить її,
а хто її любить, той ніколи не перестає вчитися»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Округлення натуральних чисел і десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.7 блоку № 8.
- Дай відповіді на питання:
- Дай визначення десятковому дробу.
- З чого складається десятковий дріб?
- Які числа можна записати у вигляді десяткового дробу?
- Назвіть розряди дробової частини десяткового дробу.
- Округлюючи натуральне число до певного розряду всі числа, що йдуть за ним замінюють …
- Якщо перша за цим розрядом цифра 5, 6, 7, 8, 9, то останню цифру …
- Якщо перша наступна за розрядом цифра 0, 1, 2, 3, 4, то останню цифру …
- Як округлюють десяткові дроби?
Завдання 2.
Усно розв’яжи вправи:
- Прочитай наближені рівності і поясни, до якого розряду округлили десятковий дріб:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
- Прочитай наближені рівності і поясни, до якого розряду округлили натуральне число:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 208 підручника: 1206, 1207 (1, 3), 1213.
Завдання 4.
- Виконай письмово вправи, стор.209 підручника: 1217, 1224, 1221.
- Виконай усно вправи, запропоновані вчителем.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 5.
- У змаганнях з бігу перші чотири місця посіли спортсменки, які показали такий час: 6,53 хв; 6,57 хв; 7,18 хв та 7,25 хв. Дарина фінішувала після Ірини, але перед Галиною. Марина бігла найшвидше. У якому порядку фінішували спортсменки?
- Знайди пропущене число:
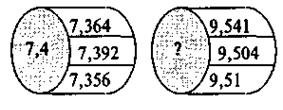
- Оформи правило округлення десяткових дробів у вигляді схеми.
- Запиши 5 прикладів зі свого досвіду, де використовуються наближені значення.
Завдання 6.
Виконайте завдання практичної роботи, запропонованої вчителем.
Практична робота
- Округліть числа до десятків. Використовуйте координатний промінь для допомоги.

- Округліть числа до сотень.

- За готовим прикладом виконайте наступне завдання.
Приклад: Місіс Спенсер, директор школи, купила книги та зошити за 547 доларів, олівці за 38 доларів і крейду за 31 долар. Ми можемо округлити ці числа до десятків і додати: $ 550 + $ 40 + $ 30 = $ 620. Ї загальний рахунок дорівнює приблизно 620 доларів.
|
Комп’ютер 296 доларів, стіл 188 доларів Комп’ютер приблизно _________________ Стіл приблизно ______________________ Загальна сума приблизно _________________ |
Тенісна ракетка 123 долари, м’ячі 38 доларів Тенісна ракетна приблизно ________________ М’ячі приблизно ____________________ Загальна сума приблизно __________________
|
|
Фільм 29 доларів, плеєр 99 доларів, штани 32 долари Фільм приблизно __________________________ Плеєр приблизно __________________________ Штани приблизно _________________________ Загальна сума приблизно ___________________
|
Принтер 65 доларів, папір 13 доларів, чорнило для принтера 117 доларів Принтер приблизно _________________________ Папір приблизно ___________________________ Чорило приблизно __________________________ Загальна сума приблизно ____________________ |
- Запишіть попереднє і наступне «кругле число», потім округліть дане число.
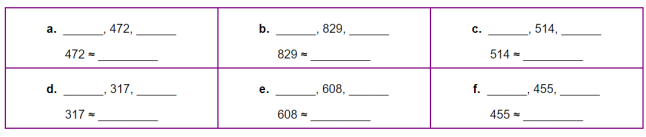
- Анна хоче купити велосипед за 129 доларів. Округліть це число до десятків. _________
Вона заробляє 30 доларів кожного тижня. Скільки вона заробить за 2 тижні? ____________________
Скільки за 3 тижні? ___________________________________
Скільки тижнів їй вистачить, щоб купити велосипед? _____________________________________
-
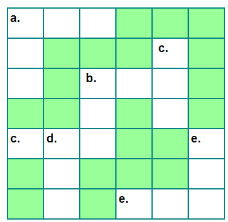 Округліть кожне число до десятків. Розмістіть кожне число в головоломку з перехресними числами.
Округліть кожне число до десятків. Розмістіть кожне число в головоломку з перехресними числами.
|
Через: |
Вниз: |
|
а. 633 |
а. 655 |
|
b. 796 |
b. 819 |
|
c. 447 |
c. 397 |
|
d. 54 |
d. 512 |
|
e. 306 |
e. 911 |
Уроки №9 – 11
«Той, хто не любить своєї
країни, нічого любити не може»
Д. Байрон
Фронтальне опрацювання матеріалу
Додавання і віднімання десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку №8.
- Дай відповіді на питання:
- Що називають десятковим дробом?
- Які розряди дробової частини десяткового дробу вам відомі?
- Як додавати десяткові дроби?
- За яким правилом віднімати десяткові дроби?
- Коли десятковий дріб округлюють до цілої частини, то що роблять з цифрами дробової частини?
- Якщо перша з відкинутих цифр десяткового дробу 5, 6, 7, 8, 9, то останню цифру, яку залишають, …
- Якщо десяткові дроби мають різні цілі частини, то як їх порівняти?
- Із двох дробів з однаковими цілими частинами, більшим буде той дріб у якого…
Завдання 2.
- Усно виконай додавання і віднімання:
1) 1,2 + 2,4 = 5) 9,7 – 5,1 =
2) 4,6 + 3,7 = 6) 7,8 – 0,2 =
3) 2,5 + 5,5 = 7) 5,4 – 2,5 =
4) 3,5 + 4,4 = 8) 3,9 – 3,7 =
- Виконай усно вправу, запропоновану вчителем.
- Виконай усно вправи, стор. 212 підручника: 1234, 1236.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Виконай письмово вправи, стор. 212 – 213 підручника: 1237; 1240; 1243 (1, 3, 5, 7, 9); 1246 (2, 4); 1249.
3.2. Виконай письмово вправи, стор. 214 – 215 підручника: 1256 (1, 3); 1262; 1289.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ
Завдання 4.
 Письмово виконай вправи:
Письмово виконай вправи:
- Задача-рецепт
Для приготування крему слід узяти вершки, сметану і цукрову пудру. Сметана і вершки важать 84,47 кг, а цукрова пудра і вершки – 79,31 кг. Скільки окремо вершків, сметани і цукрової пудри міститься у 102,08 кг крему?
- Гра «Хто швидше»
Друкуючи завдання, я випадково пропустила в числах коми.
Завдання. Відновити записи:
- 52 + 18 = 7;
- 74 – 24 = 5;
- 736 – 336 = 4;
- 725 + 275 = 10.
Завдання 5.
Виконайте практичну роботу, запропоновану вчителем.
Практична робота
- Знайти пропущені числа.
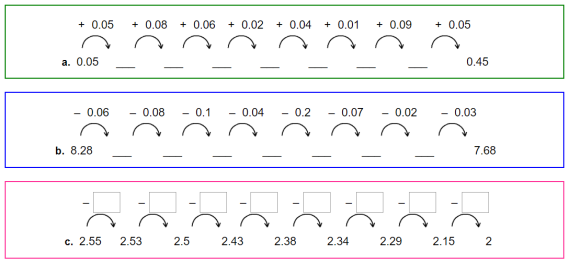
- Виконайте віднімання. Зверніть увагу на дроби, в яких неоднакова кількість знаків. Додайте до них нулі, щоб кількість знаків стала однаковою.

- Виконайте додавання і віднімання, щоб відшукати пропущені числа.

- З’ясуйте, що було виконано додавання чи віднімання і відшукайте пропущені числа.

- Перетворіть звичайні дроби в десяткові за зразком і виконайте дії.

![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Округли числа до: 1) десятих – 5,471; 2) сотих – 1,197; 3) сотень – 1439,3.
-
Розв’яжи рівняння
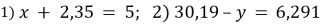 .
.
-
Знайди значення виразу
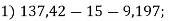
![]()
-
Обчисли найзручнішим способом:
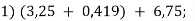
![]()
-
 Першого дня туристи пройшли 12,7 км, а другого – на 0,8 км більше, ніж першого, третього – на 6,8 км менше, ніж другого дня. Скільки кілометрів пройшли туристи за три дні?
Першого дня туристи пройшли 12,7 км, а другого – на 0,8 км більше, ніж першого, третього – на 6,8 км менше, ніж другого дня. Скільки кілометрів пройшли туристи за три дні?
-
Розв’яжи рівняння:
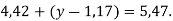
- У трьох мішках міститься 151,4 кг цукру. У першому і другому разом 89,1 кг, а у другому і третьому — 100,2 кг. Скільки кілограмів цукру в кожному мішку?
Урок №13
«Добрий розум приносить приємність»
Книга приповістей Соломонових 13 :15
Внутрішньопредметне узагальнення матеріалу
Десяткові дроби. Додавання і віднімання десяткових дробів
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
- Повтори блок № 8.
- Дай письмово відповідь на питання, запропоновані вчителем.
Завдання 2.
Усно виконай вправи:
-
Запиши у вигляді десяткового дробу: 1)
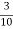 ; 2)
; 2) 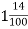 .
.
|
А |
Б |
В |
Г |
Д |
|
1) 0,3; 2) 0,114 |
1) 0,3; 2) 11,4 |
1) 0,3; 2) 1,14 |
1) 0,3; 2) 11,04 |
1) 0,03; 2) 1,014 |
- Запиши в метрах 12 см.
|
А |
Б |
В |
Г |
Д |
|
0,12 м |
1,2 м |
0,12 м |
0,012 м |
Інша відповідь |
-
Обчисли: 1 ) +
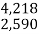 2) –
2) – 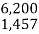
|
А |
Б |
В |
Г |
Д |
|
1) 6,708; 2) 4,853 |
1) 6,808; 2) 4,743 |
1) 6,708; 2) 5,743 |
1) 6,78; 2) 4,853 |
1) 6,608; 2) 5,853 |
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 3.
Письмово виконай вправи:
- Запиши десяткові дроби у порядку їх спадання: 0,24; 0,248; 0,31; 0,048; 1,001.
-
Виконай дії: 1)
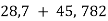 ; 2)
; 2) 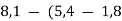 ).
).
-
Розв'яжи рівняння: 1)
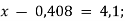 2)
2) 
- Яка довжина третьої сторони трикутника, якщо перша сторона дорівнює 2,3 м, друга на 0,4 м менша за першу, а периметр трикутника дорівнює 10,5 м?
- У трьох ящиках міститься 151,4 кг цвяхів. У першому та третьому ящиках міститься 89,1 кг, а в другому та третьому – 100,2 кг. Скільки кілограмів цвяхів у кожному ящику?
Завдання 4 (додаткове).
Письмово виконай вправи:
- У дно річки забили бетонні палі завдовжки 9,4 м так, що 3,8 м було у землі, а 1,2 м – над водою. Яка глибина річки у цьому місці?
- Швидкість течії річки 2,1 км /год, а швидкість катера проти течії - 10,7 км/год. Яка швидкість катера за течією річки?
Тема №9. Множення та ділення десяткових дробів
Урок №1

Множення та ділення десяткових дробів
«Отож, уважай, щоб те світло,
що в тобі, не сталося темрявою!»
Луки 11:35
Питання
- Множення десяткових дробів.
- Ділення десяткового дробу на натуральне число.
- Ділення на десятковий дріб.
Література
Істер О.С. Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – §§38 – 41, ст. 220 – 244.
|
||
|
1.1 |
Десяткові дроби множать за таким правилом: 1) помножити їх як натуральні числа, не звертаючи уваги на коми; 2) у добутку відокремити справа комою стільки цифр, скільки їх мають після коми обидва множники разом. |
|
|
1.2 |
Щоб помножити десятковий дріб на 10, 100, 1000 і т. д., треба в цьому дробі перенести кому вправо відповідно на 1, 2, 3 і т. д. цифр. |
|
|
1.3 |
Щоб помножити десятковий дріб на 0,1; 0,01; 0,001 тощо достатньо в цьому дробі перенести кому вліво відповідно на 1, 2, 3 і т. д. цифри. |
|
|
1.4 |
При множенні десяткових дробів справджуються усі вивчені раніше властивості множення:
|
|
|
||
|
2.5 |
Щоб поділити десятковий дріб на натуральне число потрібно:
|
|
|
2.6 |
Щоб поділити десятковий дріб на 10, 100, 1000 і т.д. треба в цьому дробі перенести кому вліво відповідно на 1, 2, 3 і т.д. цифри. |
23,4 : 10 = 2,34 5 : 100 = 0,05 138,24 : 1000 = 0,13824 |
|
||
|
3.7 |
Основна властивість частки якщо ділене й дільник помножити або поділити на одне й те саме натуральне число, то частка не зміниться. |
|
|
3.8 |
Щоб поділити число на десятковий дріб, треба в діленому і дільнику перенести кому вправо на стільки цифр, скільки їх є в дільнику; після чого виконати ділення на натуральне число. |
|
|
3.9 |
Щоб поділити десятковий дріб на 0,1; 0, 01; 0,001 і т.д. треба в цьому дробі перенести кому вправо відповідно на 1, 2, 3 і т.д. цифри. |
23,4 : 0,1 = 234 5 : 0,001 = 5000 138,24 : 0,01 = 13824 |
Уроки №2 – 4
«Якщо відразу немає
успіху, то спробуй ще і ще»
Джоан Хіксон, британська актриса
Фронтальне опрацювання матеріалу
Множення десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 1.3 блоку № 9.
- Дай відповіді на питання:
- Що таке десятковий дріб?
- Як перемножити два десяткових дроби?
- Як помножити десятковий дріб на розрядну одиницю 10; 100; 1000…?
- Як помножити десятковий дріб на розрядну одиницю 0,1; 0,01; 0,001…?
- Назвіть та сформулюйте основні закони множення.
Завдання 2.
Усно виконай вправи:
- Стор. 222 підручника: 1305 (1, 3, 5, 7); 1306 (2, 4, 6).
- Виконай усно вправи, запропоновані вчителем (презентація).
- Який знак слід поставити між числами 4 і 5, щоб вийшло число більше 4 і менше 5?
- Що спільне у рівняння і у дерева?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Розглянь приклади 1 – 3, стор. 221 підручника. Використай розглянуті приклади під час розв’язування вправ.
- Виконай письмово вправи, стор. 222 підручника: 1309 (1, 3, 5, 7); 1313; 1315 (2, 4, 6); 1318; 1320 (2); 1323; 1327 (1, 3).
- Пригадай властивості множення. Розглянь запропоновані вчителем приклади їх застосування.
- Виконай письмово вправи, стор. 224 підручника: 1331 (2, 4); 1333; 1336 (1, 3); 1338 (2, 4); 1335.
- Виконай письмово вправу, запропоновану вчителем (презентація).
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
Виконай письмово вправи, стор. 225 підручника: 1344; 1347; 1349.
Урок №5
«Тоді лише пізнається
цінність часу, коли він утрачений»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Окремі випадки множення десяткових дробів
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
-
 Повтори тези 1.1 – 1.4 блоку № 9.
Повтори тези 1.1 – 1.4 блоку № 9.
- Усно дай відповідь на питання:
- Як помножити десяткові дроби?
- Як помножити десятковий дріб на 10, 100, 1000 і т.д.?
- Як помножити десятковий дріб на 0,1; 0,01; 0,001 і т.д.?
Завдання 2.
От з’явився в нас у класі
Веселунчик клоун Вася.
Він прокинувсь на світанні
І приніс Вам запитання.
- Обчисли: 1) 2 · 100; 2) 34 · 10; 3) 1300 · 10.
- Не виконуючи множення вкажи найбільшу кількість десяткових знаків у добутку:
|
А |
Б |
В |
Г |
|
|
|
|
|
- Виконуючи множення 4,356 · 18 одержали цифри 78408. Постав кому та прочитай результат.
Завдання 3.
Вибери правильну відповідь:
- 0,0345 · 1000.
|
А |
Б |
В |
Г |
|
0,345 |
3,45 |
34,5 |
345 |
- 5,25 · 0,01.
|
А |
Б |
В |
Г |
|
52,5 |
525 |
0,525 |
0,0525 |
- 0,034 · 10.
|
А |
Б |
В |
Г |
|
0,34 |
0,0034 |
3,4 |
34 |
- 12,3 · 0,001.
|
А |
Б |
В |
Г |
|
0,123 |
0,0123 |
1,23 |
1230 |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Розв’язування прикладів з листів від Незнайка і Віллі Вонка.
Завдання 5.
Вирази у вказаних одиницях вимірювання і розшифруй вислів:
- 7,8 кг у грамах;
- 7,8 грн. у копійках;
-
 3,25 км у метрах;
3,25 км у метрах;
- 3,25 ц у кілограмах;
- 0,16 т у кілограмах;
- 0,16 а у м2.
Завдання 6.
Клоун Вася йшов до вас,
А надворі дощ якраз.
Тому числа намочились,
В картках плями появились.
Тож швиденько поміркуйте,
Й числа вправно намалюйте.
![]()
![]()
35,1 · = 0,351 436 · = 0,436
![]()
![]()
6,58 · = 0,658 65,8 · = 6,58
Завдання 7.
Знайди значення виразів та дізнайся ім’я козацького ватажка, який став улюбленим серед козаків.
![]() А
А
![]() Н
Н
![]() Р
Р
![]() І
І
![]() К
К
![]() О
О
![]() В
В
![]() С
С
Завдання 8.
Вовк побіг за Зайцем, коли відстань між ними була 100 м. Заєць біг зі швидкістю 0,01 км/с, Вовк – зі швидкістю 0,006 км/с. Яка відстань буде між ними через 10 с? Чи зможе Вовк наздогнати Зайця?
Урок №6
Щоб наш урок був плідним, будемо:
не просто слухати, а чути;
не просто дивитися, а бачити;
не просто відповідати, а міркувати;
дружно й плідно працювати!
Індивідуальне опрацювання матеріалу
Окремі випадки множення
Виконання практичної роботи «Тема 8 робочий зошит «Я дослідник»
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Знайди периметр і площу квадрата, сторона якого дорівнює 4,2 см.
-
Спрости вираз
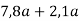 і знайди його значення
і знайди його значення 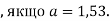
-
Виконай дії:
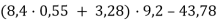 .
.
- Обчисли об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 1,7 м; 0,4 м; 4,6 м.
-
Спрости вираз
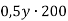 і знайди його значення, якщо
і знайди його значення, якщо 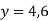 .
.
- Швидкість течії річки – 1,7 км/год, власна швидкість човна – 18,5 км/год. Знайди, яку відстань пропливе човен за 2,6 год руху проти течії і 1,5 год руху за течією.
Уроки №8, 9
«Як нерозумно випрохувати те, чого можеш сам досягти»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Ділення десяткового дробу на натуральне число
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.6 блоку № 9.
- Усно дай відповіді на питання:
- Як помножити два десяткові дроби?
- Які ти знаєш властивості множення?
- Як помножити десятковий дріб на 10, 100, 1000 і т.д.?
- Як помножити десятковий дріб на 0,1; 0,01; 0,001 і т.д.?
- Як поділити десятковий дріб на натуральне число?
- Як поділити десятковий дріб на 10, 100, 1000 і т.д.?
Завдання 2.
- Розглянь приклади 1, 2, 3 на стор. 230 підручника.
- Усно дай відповідь на питання:
- Що ставимо в частці, якщо ціла частина діленого менша від дільника?
- Яку ще дію можна виконувати за правилом ділення десяткового дробу на натуральне число?
-
Як звичайний дріб перетворити у десятковий?
- Виконай усно вправи, стор. 231 підручника: 1374, 1375.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Виконай письмово вправи, стор. 232: 1380, 1382, 1387.
- Виконай письмово (самостійно) вправи, стор. 232 підручника: 1381, 1383.
- Виконай письмово вправи, стор. 232 – 236 підручника: 1390 (1, 3, 5), 1396, 1400, 1408 (1, 3, 5), 1413, 1418; 1428.
Уроки №10 – 12
«Блажен той муж, воістину блажен,
котрий не був ні блазнем, ні вужем.
Котрий вовік ні в празники, ні в будні
не піде на збіговиська облудні»
Ліна Костенко, Псалом 1:1
Фронтальне опрацювання матеріалу
Ділення на десятковий дріб
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Прочитай уважно тези блок № 9.
- Усно дай відповідь на питання:
- Як помножити десяткові дроби?
- Як поділити десятковий дріб на натуральне число?
- Як поділити число на десятковий дріб?
- Як помножити число на 10, 100, 1000 і т.д.?
- Як помножити число на 0,1; 0,001; 0,001 і т.д.?
- Як поділити десятковий дріб на 10, 100, 1000 і т.д.?
- Як поділити десятковий дріб на 0,1; 0,01; 0.001 і т.д.?
- Як читається основна властивість частки?
Завдання 2.
Усно виконай вправи:
- Вправа 1438, стор. 237 підручника.
- Виконай ділення: 1) 65,2 : 10; 2) 65,2 : 100; 3) 65,2 : 1000.
- Виконай ділення: 1) 6,25 : 0,1; 2) 6,25 : 0,01; 3) 6,25 : 0,001.
-
Виконай дії та дізнайся як називається багаторічна рослина, яка росте в Південній Америці і розцвітає один раз в житті:
1) 8,1 : 0,09 ; 2) 2,86 : 100; 3) 49,5 : 0,1; 4) 4 : 16; 5) 2,7 : 0,2.
|
0,25 В |
90 А |
13,5 А |
|
0,9 О |
495 А |
0,0286 Г |
ІІ. Відпрацювання практичних умінь та навичок
Завдання 3.
Письмово виконай вправи, стор. 238 підручника: 1441 (2, 4, 6, 8); 1450; 1456 (1, 3); 1461 (1, 3); 1468; 1469; 1478 (1, 2, 3); 1482 (2, 4); 1487.
Завдання 4.
Письмово виконай вправи:
- Буратіно зробив обчислення, проте випадково сплутав всі відповіді. Допоможи йому і ти дізнаєшся назву найбільшої квітки:
а) 68,4 : 9 1) 1,8 ф
б) 12,43 : 100 2) 0,1243 а
в) 0,1242 : 0,069 3) 7,6 р
г) 45,69 :100 4) 1,9 з
д) 34,3 :1,4 5) 24,5 е
е) 0,1387 : 0,073 6) 151 і
є) 15,1 : 0,1 7) 0,4569 л
ж) 86,02 : 0,2 8) 430,1 я
- Виконай дії і ти дізнаєшся, який з наших птахів літає найшвидше: (4 – 2,6) · 4,3 + 1,08 : 1,2 – 0,9.
- Маса колібрі — найменшої пташки на Землі — 1,8 г, що у 0,00002 більше маси страуса — найбільшого птаха. Знайди масу страуса.
- У двох кошиках і 4 однакових ящиках складено 73,72 кг апельсинів. У кожному кошику по 6,4 кг апельсинів. Скільки апельсинів у кожному ящику?
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Письмово виконати вправи, стор. 242 підручника: 1492; 1494.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Обчисли:
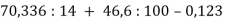 .
.
-
Знайди корінь рівняння:
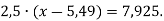
-
 Площа прямокутника дорівнює 13,12 см2, одна з його сторін – 4,1 см. Знайди периметр прямокутника.
Площа прямокутника дорівнює 13,12 см2, одна з його сторін – 4,1 см. Знайди периметр прямокутника.
- З однієї квітки одночасно злетіло в протилежних напрямках дві бджоли. Через 0,08 год відстань між ними була 4,4 км. Швидкість однієї бджоли 28,8 км/год. Знайти швидкість другої бджоли.
Уроки №14, 15
«Учитися можна тільки весело... Щоб
переварити знання, їх потрібно вживати з апетитом»
Анатоль Франс, французький письменник
Фронтальне опрацювання матеріалу
Розв’язування вправ на всі дії з десятковими дробами
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блоки № 8, № 9.
- Усно дай відповідь на питання:
- Що називають десятковим дробом?
- Які дії ти вмієш виконувати над десятковими дробами?
- Як додати (відняти) десяткові дроби?
- Як помножити десяткові дроби?
- Як поділити десятковий дріб на натуральне число?
- Як поділити число на десятковий дріб?
- Як помножити десятковий дріб на 10, 100, 1000 і т.д.?
- Як помножити десятковий дріб на 0,1; 0,01; 0,001 і т.д.?
- Як поділити десятковий дріб на 10, 100, 1000 і т.д.?
- Як поділити десятковий дріб на 0,1; 0,01; 0,001 і т.д.?
- Як звичайний дріб записати у вигляді десяткового дробу?
- Сформулюй правило округлення натуральних чисел.
- Сформулюй правило округлення десяткових дробів.
Завдання 2.
Усно виконай вправи:
- Обчисли усно:
-
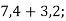 6)
6) 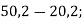
-
 7)
7) 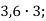
-
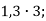 8)
8) 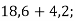
-
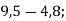 9)
9) 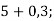
-
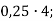 10)
10) 
- Округли: 1) до десятих: 12,88; 0,33; 2) до сотих: 5,678; 0,781; 3) до десятків: 44,7; 68,3; 4) до сотень: 375,2; 1342,1; 5) до одиниць: 371,8; 59,3.
-
Встанови відповідність між звичайними та десятковими дробами:
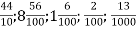 ; 1,06; 4,4; 0,013; 8,56; 0,02.
; 1,06; 4,4; 0,013; 8,56; 0,02.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Ознайомся з інформацією про Червону книгу України (презентація).
- Розгадай кросворд і у виділеному стовпці прочитай назву рослини, занесеної до Червоної книги (презентація).
Завдання 4.
Письмово виконай вправи:
- Обчисли значення виразу та прочитай назву найбільшої змії України, занесеної до Червоної книги: (1,184 : 3,2 + 0,832 : 0,4) : 0,5 + 1,5.
|
6,4 |
2,08 |
4,9 |
2,45 |
0,37 |
|
З |
О |
О |
Л |
П |
- Розв’яжи рівняння та прочитай назву найбільшої тварини України, занесеної до Червоної книги: 1) (0,8 х + 9,4) ∙ 0,2 = 1,928; 2) 6,8у – 2,3у + 24,6 = 47,55.
|
0 |
1 |
3 |
5 |
|
З |
Р |
У |
Б |
- Швидкість польоту стрижа – 1600 м/хв, швидкість польоту шпака становить 0,75, а яструба – 0,44 швидкості польоту стрижа. Знайди швидкість польоту яструба і шпака.
- В заповіднику Асканія-Нова охороняється близько 30 видів ссавців, що дорівнює 0,75 видів тварин, занесених до Червоної книги України. Скільки всього видів тварин занесені до Червоної книги України?
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Обчисли значення виразів і ти потрапиш ще на одну сторінку Червоної книги:
1) 0,12 : 2 + 4,1; 5) (19,85 + 4,65) : 5;
2) 19,56 : (3,2 + 4,95); 6) 7,224 : 0,301 – 18,6;
3) 0,308 : 0,14 + 1,08; 7) (7,6 – 5,78) : 9,1.
4) 21,5 – 7,2 : 0,6;
|
9,5 |
2,4 |
3,28 |
4,9 |
5,4 |
4,16 |
0,2 |
|
Ь |
Е |
Л |
Ф |
І |
Д |
Н |
Урок №16
«В собі самому шукай справжніх благ»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Задачі на всі дії з десятковими дробами
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 9.
- Усно дай відповіді на питання:
- Які числа називають десятковими дробами?
- Які дії ви вмієте виконувати над десятковими дробами?
- Як помножити десяткові дроби?
- Сформулюйте правило округлення десяткових дробів.
- Як поділити десятковий дріб на натуральне число?
- Як поділити десятковий дріб на десятковий дріб?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 2.
Виконай усно вправи:
-
Запиши у вигляді десяткового дробу
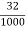 .
.
|
А |
Б |
В |
Г |
|
0,32 |
3,2 |
0,032 |
0,0032 |
-
Обчисли:
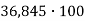 .
.
|
А |
Б |
В |
Г |
|
0,36845 |
3,6845 |
368,45 |
3684,5 |
-
Виконай ділення
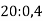 .
.
|
А |
Б |
В |
Г |
|
5 |
0,5 |
50 |
500 |
Завдання 3.
Виконай письмово вправи:
- Округли число:
- 81,58 до десятих;
-
32,643 до сотих.
-
Розв’яжи рівняння:
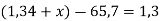 .
.
-
Спрости вираз і обчисли його значення
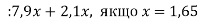 .
.
-
Обчисли значення виразу:
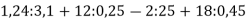 .
.
- Відстань між двома пристанями дорівнює 260,4 км. Від цих пристаней назустріч один одному одночасно вирушили два катери, які зустрілись через 2,4 год після початку руху. Один катер рухався зі швидкістю 48,3 км/год. Знайдіть швидкість другого катера.
-
Розв’яжи рівняння:
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Округли:
- до десятих число 8,263;
- до сотих число 11,958.
-
Спрости вираз
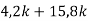 і обчисли його значення,
і обчисли його значення, 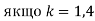 .
.
-
Розв’яжи рівняння:
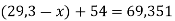 .
.
-
Обчисли:
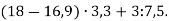
-
Обчисли значення виразу:
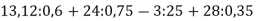 .
.
- Відстань між двома пристанями дорівнює 88,2 км. Від цих пристаней назустріч один одному одночасно вирушили два моторних човни, які зустрілись через 1,5 год після початку руху. Один із них рухався зі швидкістю 28,3 км/год. Знайдіть швидкість другого човна.
Урок №18
«Хто любить навчання, той любить
пізнання, а хто докір ненавидить, той нерозумний»
Книга приповістей Соломонових 12 : 1
Внутрішньопредметне узагальнення матеріалу
Множення і ділення десяткових дробів
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
1.1. Повтори блок № 9.
1.2. Письмово дай відповіді на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
2.1. Виконай множення: 7,82 ∙ 1000.
|
А |
Б |
В |
Г |
|
78,2 |
78200 |
782 |
7820 |
2.2. Виконай ділення: 5412,92 : 100.
|
А |
Б |
В |
Г |
|
541,292 |
0,541292 |
54,1292 |
5,41292 |
2.3. Довжина прямокутника дорівнює 80 см. Знайдіть ширину прямокутника, якщо вона становить 0,6 від довжини.
|
А |
Б |
В |
Г |
|
4,8 см |
1,6 см |
16 см |
48 см |
Завдання 3.
Письмово виконай вправи:
- Виконай ділення: 1) 0,048 : 16; 2) 39 : 4; 3) 73,8 : 9.
- Обчисли, використовуючи зручний спосіб: 1) 0,5 ∙ 2,8 ∙ 2; 2) 12,5 ∙ 48,6 ∙ 0,8.
-
Розв'яжи рівняння:
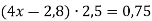 .
.
- Катер проплив за течією річки 63,35 км і 41,75 км проти течії річки. Скільки часу рухався катер, якщо його власна швидкість дорівнює 34,8 км/год, а швидкість проти течії річки – 33,4 км/год?
- Знайди значення виразу: (15,4 : 77 + 113,6 ∙ 2,5) – 2,46 : 60.
Тема №10. Відсотки. Середнє арифметичне
Урок №1

Відсотки. Середнє арифметичне
«…математика безмежно різноманітна, як світ…»
М.П. Єругін, білоруський математик
Питання
- Поняття про відсотки.
- Знаходження відсотків від даного числа.
- Знаходження числа за його відсотками.
- Середнє арифметичне. Середнє значення величини.
Література
Істер О.С. Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – §§42 – 44, ст. 244 – 260.
|
1. Поняття про відсотки |
||
|
1.1 |
Дріб Відсоток позначають значком %. |
1% = |
|
1.2 |
Щоб виразити десятковий дріб у відсотках, потрібно його помножити на 100%. |
0,83 = 0,83 ∙ 100% = 83% 0,02 = 0,02 ∙ 100% = 2% |
|
1.3 |
Щоб виразити відсотки десятковим дробом, потрібно їх поділити на 100%. |
48% = 48% : 100% = 0,48 4% = 4% : 100% = 0,04 |
|
1.4 |
Щоб перетворити звичайний дріб у відсотки, треба спочатку перетворити його у десятковий, а потім помножити отриманий десятковий дріб на 100. |
|
|
1.5 |
Все, ціле, про що йде мова в задачі, становить 100%. |
Всі учні класу – 100% Весь шлях – 100% |
|
1.6 |
Запам’ятай!
|
|
|
|
2. Знаходження відсотків від даного числа |
|
|
2.7 |
1 спосіб Щоб знайти відсотки від числа, потрібно це число поділити на 100 (знайти 1%), а потім помножити на число відсотків. |
1. Знайди 12 % від 500. 500 : 100 ∙ 12 = 60 2. Знайди 40 % від 3 грн.. 3 : 100 ∙ 40 = 1,2 (грн.) |
|
2.8 |
2 спосіб Щоб знайти відсотки від числа, потрібно виразити відсоток десятковим дробом і помножили дане число на цей дріб. |
1. Знайди 12 % від 500.
2. Знайди 40 % від 3 грн.. 40 % = 0,4; 3 ∙ 0,4 = 1,2 (грн.) |
|
|
3. Знаходження числа за його відсотками |
|
|
3.9 |
1 спосіб Щоб знайти число за його відсотками, потрібно число, яке становить частину шуканого числа, поділити на відповідні йому відсотки (знайти 1%) і помножити на 100.
|
1. Знайди число, якщо 15% його становлять 30. 30 : 15 ∙ 100 = 200. 2. 8 учнів відсутні в школі. Це становить 25% всіх учнів. Скільки учнів у класі? 8 : 25 ∙ 100 = 32 (учні). |
|
3.10 |
2 спосіб Щоб знайти число за його відсотками, потрібно виразити відсоток десятковим дробом і поділити дане число на цей дріб. |
1. Знайди число, якщо 15% його становлять 30. 15 % = 0,15; 30 : 0,15 = 200. 2. 8 учнів відсутні в школі. Це становить 25% всіх учнів. Скільки учнів у класі? 25 % = 0,25; 8 : 0,25 = 32 (учні) |
|
4. Середнє арифметичне. Середнє значення величини |
||
|
4.11 |
Середнім арифметичним кількох чисел називається число, знайдене при діленні суми цих чисел на їх кількість. |
Знайди середнє арифметичне чисел 2; 3; 7: (2 + 3 + 7): 3 = 12 : 3 = 4. |
|
4.12 |
Щоб знайти середню швидкість руху, треба весь пройдений шлях поділити на весь затрачений час. Аналогічно можна знаходити середнє значення деякої величини. |
Пішохід за три години пройшов відповідно 4,7 км; 4,9 км і 4,2 км. Яка середня швидкість пішохода за цей час?
|
Уроки №2, 3
«Блаженна людина, що мудрість
знайшла і людина, що розум одержала»
Книга приповістей Соломонових 3 : 13
Фронтальне опрацювання матеріалу
Поняття відсотка. Знаходження відсотків від числа
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 2.8 блоку № 9.
- Дай відповіді на питання:
- Що називають відсотком?
- Як ще називають відсоток?
- Як виразити десятковий дріб у відсотках?
- Як виразити відсотки десятковим дробом?
- Як перетворити звичайний дріб у відсотки?
- Що становить 100 %?
- Як знайти відсотки від числа?
Завдання 2.
Усно виконай вправи:
- Подай відсотки у вигляді десяткового дробу:
|
3 % |
21 % |
30 % |
56 % |
80 % |
110 % |
14, 6 % |
|
|
|
|
|
|
|
|
- Запиши десятковий дріб у вигляді відсотків:
|
0,05 |
0,6 |
8,6 |
1,3 |
0,124 |
0,71 |
0,48 |
|
|
|
|
|
|
|
|
- Яка величина приймається за 100 %, коли відомо, що:
- 35% усіх учнів класу становлять дівчатка;
- молоко дає 25% вершків;
- в перший день скопали 30% городу;
- з пшениці виходить 80% борошна;
- маса кошеняти складає 15% маси кішки;
- нікелева руда містить 1,3% нікелю;
-
з чайного листа після сушіння виходить 4,2% чаю?
- Скільки відсотків фігури зафарбовано?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Яку частину фігури становить 50 %; 25 %; 75 %?
- Обчисли: 1) 50 % від числа 40; 2) 25 % від числа 40; 3) 75 % від числа 40; 4) 100 % від числа 40.
- Як називають соту частину: 1) гектара; 2) століття; 3) гривні; 4) метра?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 247 підручника: 1503 (1, 3, 5); 1505 (2, 4, 6); 1507; 1509.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
 Виконати завдання практичної роботи, запропонованої вчителем.
Виконати завдання практичної роботи, запропонованої вчителем.
Практична робота
- Зафарбуй 100% квадрата будь-яким кольором.
- Чи можлива ситуація? Якщо так, постав у клітинку поряд із твердженням знак «+», якщо ні – знак «-».
-
101% учнів класу займаються спортом

-
За два дні Маринка прочитала 150% книги

-
За два дні Маринка прочитала 100% книги

-
Вовчик за один день з’їв 90% пиріжків, що спекла бабуся

- Скориставшись зразком, подай відсотки у вигляді десяткового дробу.

- Скориставшись зразком, подай число у вигляді відсотків.

- Заповни порожні місця у таблиці.

- Заповни пропуски так, щоб на однакових геометричних фігурах була записана одна й та сама величина: у вигляді відсотків і у вигляді десяткового дробу.

Урок №4
«Хто стереже свої уста й свого
язика, той душу свою зберігає від лиха»
Крига приповістей Соломонових 21:23
Фронтальне опрацювання матеріалу
Знаходження числа за його відсотком
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.10 блоку №10.
- Усно дай відповіді на питання:
- Що називають відсотком?
- Як ще називають відсоток?
- Як виразити десятковий дріб у відсотках?
- Як виразити відсотки десятковим дробом?
- Як перетворити звичайний дріб у відсотки?
- Що становить 100 %?
- Як знайти відсотки від числа?
- Як знайти число за його відсотками?
Завдання 2.
Виконай усно вправи:
2.1. Доповни записи

2.2. Розглянь рисунки, поміркуй, запиши відповідні числа
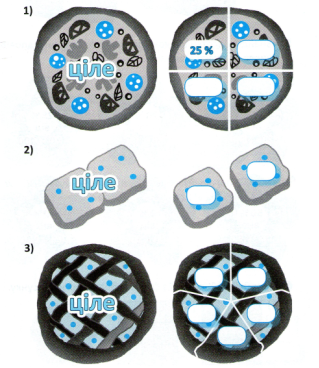

2.3. Зафарбуй 40% усіх повітряних кульок, що зображені на рисунку, жовтим кольором, 10% - рожевим, 25% - зеленим, 10% - синім. Скільки кульок залишилось незафарбованими?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи:
3.1. Малюк виконав 6 прикладів на множення, що дорівнює 30 % всієї домашньої роботи. Скільки прикладів у домашній роботі Малюка?
3.2. В басейн налили 1400 м3 води, що складає 35 % об’єму всього басейну. Який об’єм всього басейну?
3.3. Спортсмен готується до турніру. 78 % всіх кидків потрапило в ціль. Скільки було зроблено кидків, якщо в ціль потрапило 156 дротиків?
3.4. 60 % учнів класу поїхали на екскурсію, а 25 % учнів і ще 3 учні пішли у кіно. Скільки учнів у класі?
3.5. Робітник зробив 60 % всього завдання і ще 8 деталей, а його учень – 20 % всього завдання і 7 деталей. Скільки всього деталей зробили майстер і учень?
3.6. Троє хлопчиків знайшли в лісі 200 грибів. Микита знайшов 40 % всіх грибів, Олег 25 % грибів, які знайшов Микита, Дмитрик знайшов решту грибів. Скільки грибів знайшов Дмитрик?
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
Лікар Айболить зі своїми друзями плив на кораблі по річці Лімпопо, щоб вилікувати хворих звірів. Коли вони пропливли 60 % шляху, на них напали пірати. Але друзі перехитрили піратів, і 80 км шляху, що залишилися, пропливли на піратському кораблі. Скільки кілометрів складає весь шлях лікаря Айболита?
Урок №5
 «Приклади в навчанні корисніші за правила»
«Приклади в навчанні корисніші за правила»
Ісаак Ньютон
Фронтальне опрацювання матеріалу
Знаходження числа за його відсотком
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.10 блоку №10.
- Усно дай відповіді на питання:
- Що називають відсотком?
- Як ще називають відсоток?
- Як виразити десятковий дріб у відсотках?
- Як виразити відсотки десятковим дробом?
- Як перетворити звичайний дріб у відсотки?
- Що становить 100 %?
- Як знайти відсотки від числа?
- Як знайти число за його відсотками?
Завдання 2.
Виконайте усно вправи:
- Перетворіть дроби у відсотки: 0,13 ; 1,09; 0,8; 0,45; 0,006.
- Перетворіть відсотки у дроби: 43%; 18%; 40%; 77%; 112%.
- Витягнувши себе за чуба з болота, барон Мюнхгаузен сказав:
- Я висмикнув 120% свого волосся.
- Я висмикнув 60% свого волосся і став лисим.
- Я висмикнув 1,2% свого волосся.
- Я висмикнув 35% свого волосся, а 75% волосся, що залишилося, геть посивіло.
Які з цих висловлювань можуть бути правдивими?
-
Знайти:
1) 5 % від 300; 12; 3;
2) число, якщо 5 % його дорівнюють 700; 3.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор 252 підручника: 1549; 1560.
ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач
Завдання 4.
- Виконай письмово вправи, стор 253 підручника: 1567; 1570.
- Відтвори прямокутник, якщо на рисунку зображено:
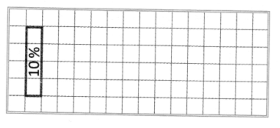
- 10% прямокутника
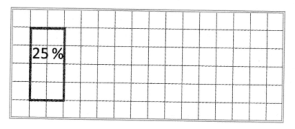
- 25% прямокутника
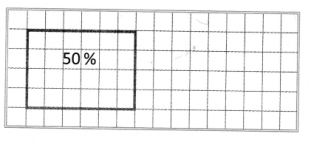
- 50% прямокутника
![]()
-
Постав поряд із твердженням позначку , якщо твердження правильне, або позначку
 , якщо твердження неправильне.
, якщо твердження неправильне.
-
Якщо 50% від довжини відрізка АВ становить 10 см, то АВ = 2 м

-
Якщо 25% від довжини відрізка АВ становить 10 см, то АВ = 4 дм

-
Якщо 20% від довжини відрізка АВ становить 5 см, то АВ = 1 м

-
Якщо 2% від довжини відрізка АВ становить 1 см, то АВ = 50 дм

Уроки №6, 7
«Хто погорджує словом Господнім, той шкодить
собі, хто ж страх має до заповіді, тому надолужиться»
Книга приповістей Соломонових 13:13
Фронтальне опрацювання матеріалу
Розв’язування задач на відсотки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.10 блоку №10.
- Усно дай відповіді на питання:
- Що називають відсотком?
- Як знайти відсотки від даного числа?
- Як знайти число за його відсотками?
- Яку ще назву має відсоток?
- Що ми приймаємо за 100% у задачі?
- Як виразити відсотки десятковим дробом?
- Як виразити десятковий дріб у відсотках?
- Як перетворити звичайний дріб у відсотки?
- Яку частину від цілого становлять 10 %; 25 %; 50 %; 75 %; 20 %?
Завдання 2.
Усно виконай вправи:
- Скільки гривень складає 1 % від 1000 грн.?
|
А |
Б |
В |
Г |
|
100 грн. |
10 грн. |
1 грн. |
0,1 грн. |
- Знайдіть 20% від числа 50.
|
А |
Б |
В |
Г |
|
5 |
10 |
20 |
15 |
- Знайти число, якщо 25% від нього дорівнює 20.
|
А |
Б |
В |
Г |
|
5 |
4 |
80 |
50 |
Завдання 3.
Усно розв’яжи вправи:
- Круг поділили на 100 рівних частин. Скільки відсотків від усього круга становлять 2, 8, 25, 80, 100 таких частин?
- Скільки відсотків від площі квадрата становить площа половини квадрата; чверті квадрата?
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 4.
Письмово розв’яжи вправи:
- Найбільша швидкість, з якою може рухатися лев, 80 км/год, що становить 125% найбільшої можливої швидкості гієни. Яка найбільш можлива швидкість гієни?
- Петрик витратив 52% своїх грошей на покупку нової книжки, 40% грошей на цукерки, після чого в нього залишилось 2,8 грн. Скільки грошей було в Петрика спочатку?
- Плід банана складається зі шкірки та м'якоті. М'якоть містить 75 % води, решта — поживні речовини. Скільки поживних речовин міститься у 480кг плодів, якщо відомо, що шкірка складає 40 % маси банана?
- На ремонт школи витратили 4340 грн. З них 35 % заплатили за роботу, а решту – за будівельні матеріали. Скільки коштували будівельні матеріали?
- У шкільній бібліотеці 1800 книжок. З них 28 % становлять книжки науково-популярної тематики, 43 % – книжки зарубіжних письменників, а решта – українських. Скільки книжок українських письменників у бібліотеці?
- Магазин протягом трьох днів продав завезену картоплю. Першого дня продали 32 % всієї картоплі, другого – 40 %, а третього – решту 224 кг. Скільки кілограмів картоплі було завезено у магазин.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 5.
Письмово розв’яжи вправи:
- Катруся з мамою купували взуття, маючи 1000 грн. Катрусі сподобались чоботи за 1200 грн., на які була знижка 17 %. Чи зможе Катруся купити чоботи?
- Баскетбольний майданчик площею 240 м² займає 15 % площі шкільного спортивного майданчика. Площа спортивного майданчика становить 32 % площі всієї шкільної ділянки. Знайди площу шкільної ділянки.
- Додали три числа. Перше число становить 25 % від суми, друге – 35 % від суми. Які числа додали, якщо третє число на 2,1 більше, ніж друге?
- 35% учасників відбіркових спортивних змагань взяли участь у районній олімпіаді, а 20% учасників районної олімпіади в кількості 28 чоловік взяли участь в обласній олімпіаді. Скільки чоловік взяли участь у відбіркових змаганнях?
- Мотоцикліст проїхав 120 км. 40% шляху він їхав шосе зі швидкістю 30 км/год, а решту шляху – ґрунтовою дорогою зі швидкістю на 20% меншою. За який час мотоцикліст проїхав всю відстань?
- В якій кількості води потрібно розчинити 400 г солі, щоб отримати 5-відсотковий розчин?
Урок №8
«Господня земля, і все, що на ній, вселенна й мешканці її»
Псалом 23:1
Індивідуальне опрацювання матеріалу
Розв’язування задач на відсотки
Виконання практичної роботи «Тема 9 робочий зошит «Я дослідник»
Урок №9
«Купи собі й не продавай правду,
мудрість, і картання та розум»
Книга приповістей Соломонових 23:23
Фронтальне опрацювання матеріалу
Відсотки. Задачі на відсотки
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези 1.1 – 3.10 блоку №10.
- Усно дай відповіді на питання:
- Що називають відсотком?
- Як знайти відсотки від даного числа?
- Як знайти число за його відсотками?
- Яку ще назву має відсоток?
- Що ми приймаємо за 100% у задачі?
- Як виразити відсотки десятковим дробом?
- Як виразити десятковий дріб у відсотках?
- Як перетворити звичайний дріб у відсотки?
- Яку частину від цілого становлять 10 %; 25 %; 50 %; 75 %; 20 %?
Завдання 2.
Усно виконай вправи:
- Скільки гривень складає 1% від 200 000 грн.?
|
А |
Б |
В |
Г |
|
200 грн. |
20 грн. |
2000 грн. |
|
- Знайди 30% від числа 150.
|
А |
Б |
В |
Г |
|
15 |
30 |
50 |
25 |
- Знайди число, якщо 25% від нього дорівнює 12.
|
А |
Б |
В |
Г |
|
120 |
75 |
480 |
48 |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
- Сплав містить 6% олова. Скільки кілограмів олова міститься в 520 кг сплаву?
- Найбільша швидкість, з якою може рухатися дельфін, 70 км/год, що становить 140% найбільшої можливої швидкості синього кита. Яка найбільш можлива швидкість синього кита?
- Бригада трактористів мала зорати 4830 га за два тижні. За перший тиждень вони зорали 47% землі. Скільки гектарів землі зорала бригада трактористів за другий тиждень?
- Сергійко з батьком та матір’ю збирали гриби. Батько зібрав 46% грибів, мати – 32%, а Сергійко – решту 66 грибів. Скільки всього грибів було зібрано?
- За три дні було продано 480 кг овочів. У перший день було продано 25% всіх овочів, що складає 60% овочів, проданих на другий день. Скільки кілограмів овочів продали на третій день?
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
 Полуниця містить 6% цукру. Скільки кілограмів цукру міститься в 48 кг полуниці?
Полуниця містить 6% цукру. Скільки кілограмів цукру міститься в 48 кг полуниці?
- Найбільша швидкість, з якою може рухатися собака, 80 км/год, що становить 320% найбільшої можливої швидкості черепахи. Яка найбільш можлива швидкість черепахи?
- До магазину завезли 400 кг картоплі. Першого дня було продано 23% завезеної картоплі. Скільки кілограмів картоплі залишилось продати?
- Сергійко з татом і мамою збирали гриби. Тато зібрав 46% всіх грибів,мама – 32%, а Сергійко – решту 44 гриби. Скільки всього грибів зібрала сім’я?
- За перший день робітник виготовив 35% всіх деталей. Це складає 70% кількості деталей, виготовлених робітником другого дня. Скільки деталей виготовив робітник на третій день, якщо за всі три дні він зробив 160 деталей?
Урок №11
«Що може бути шкідливіше за людину, котра володіє
знанням найскладніших наук, але не має доброго серця?»
Григорій Сковорода
Фронтальне опрацювання матеріалу
Середнє арифметичне
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори блок № 10.
- Усно дай відповіді на питання:
- Що називають відсотком?
- Як знайти відсотки від даного числа?
- Як знайти число за його відсотками?
- Що ми приймаємо за 100% у задачі?
- Як виразити відсотки десятковим дробом?
- Як виразити десятковий дріб у відсотках?
- Як перетворити звичайний дріб у відсотки?
- Що називають середнім арифметичним?
Завдання 2.
Усно виконай вправи, стор. 256 підручника: 1581; 1582.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Завдання 3.
Виконай письмово вправи, стор. 256 – 258 підручника: 1586; 1591; 1593; 1595; 1598; 1606, 1610.
Урок №12
«Арифметика — вхідна брама до всіх інших наук, без її пізнання
ніхто не може зробити жодного кроку вперед до храму науки»
Феофан Прокопович, український богослов, письменник, поет,
математик, філософ, ректор Київської академії (1710—1716)
Фронтальне опрацювання матеріалу
Середнє значення величини
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку №10.
- Усно дай відповіді на питання:
- Як знайти середнє арифметичне?
- Що таке відсоток? Як позначають відсотки?
- Як виразити відсотки десятковим дробом?
- Сформулюй правило знаходження відсотка від числа.
- Як знайти число за його відсотком?
- Як знайти середню швидкість і середнє значення величини?
Завдання 2.
Усно виконай вправи:
- Учню Олександру в класному журналі поставили оцінки 6 і 8. Яку ж оцінку потрібно поставити учневі за тему? А Денис мав оцінки 7, 7 і 10. Яку ж оцінку поставити Денисові?
- Знайти середнє арифметичне: 1) 5 і 7; 2) 97 і 103; 3) 38 і 12; 4) 0,2 і 2; 5) 11, 12 і 13.
- Знайти середнє арифметичне: 1) велосипеда і мотоцикла; 2) апельсина і лимона; 3) піаніно і баяна; 4) холодильника і вентилятора.
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Письмово виконай вправи:
Завдання 3.
- Накресли координатний промінь, одиничний відрізок якого дорівнює одній клітинці зошита. Познач на цьому промені точки М(3), N(2), К(7) і точку А, координата якої є середнім арифметичним координат усіх трьох заданих точок.
- Знайди невідоме число, якщо відоме число дорівнює 7,4, а їх середнє арифметичне — 8,1.
- Знайди 10% числа, яке є середнім арифметичним чисел 3,8 та 1,2.
Завдання 4.
- Температура повітря опівдні у п'ятницю була 35,1°С, у суботу вона дорівнювала 35,5°С, а в неділю становила 34,7°С. Знайди середню температуру опівдні протягом трьох днів.
- У фермера 5 корів. За 30 днів від них надоїли 4725 л молока. Скільки літрів молока в середньому дає в цього фермера одна корова за день?
- У різних магазинах міста 1 кг лимонів коштує по-різному: в першому магазині — 22 грн. 10 к., у другому — 23 грн. 20 к., а в третьому — 21 грн. 90 к. Яка середня ціна 1 кг лимонів?
- Велосипедист їхав 3 год зі швидкістю 18 км/год і 5 год зі швидкістю 16 км/год. Знайдіть середню швидкість велосипедиста протягом усього шляху.
Урок №13
«Господня земля, і все, що на ній, вселенна й мешканці її»
Псалом 23:1
Індивідуальне опрацювання матеріалу
Середнє арифметичне. Середнє значення величини
Виконання практичної роботи «Тема 10 робочий зошит «Я дослідник»
Уроки №14, 15
«Ліпше добре ім'я за багатство
велике, і ліпша милість за срібло та золото»
Книга приповістей Соломонових 22:1
Фронтальне опрацювання матеріалу
Застосування середнього арифметичного та середнього значення величини до розв’язування задач
І. Робота над засвоєнням понять, термінів і правил
Завдання 1.
- Повтори тези блоку №10.
- Усно дай відповіді на питання:
- Як знайти середнє арифметичне?
- Що таке відсоток? Як позначають відсотки?
- Як виразити відсотки десятковим дробом?
- Сформулюй правило знаходження відсотка від числа.
- Як знайти число за його відсотком?
- Як знайти середню швидкість і середнє значення величини?
Завдання 2.
Усно виконай вправи:
- Сума трьох чисел дорівнює 360. Знайди середнє арифметичне цих чисел.
|
А |
Б |
В |
Г |
|
36 |
120 |
80 |
100 |
- Вінні-Пух за перший день з’їв 3 баночки меду, за другий — 4 баночки, а за третій — аж 5 баночок. Скільки у середньому баночок меду з’їдав Вінні-Пух за день?
|
А |
Б |
В |
Г |
|
12 |
9 |
4 |
7 |
- Автомобіль за перші дві години проїхав 117 км, а за три наступні – 203 км. Скільки кілометрів в середньому він проїжджав за одну годину?
|
А |
Б |
В |
Г |
|
117 км |
204 км |
64 км |
320 км |
ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ
Письмово виконай вправи:
Завдання 3.
- Зріст волейболістів, які грали на майданчику, такий: 2 м; 1,87 м; 1,96 м; 1,98 м; 2,03 м і 1,86 м. Обчисли середній зріст цих волейболістів.
- На футбольних змаганнях команда за виграш отримує 2 бали, за поразку — 0 балів, за нічию — 1 бал. Команда «Чемпіон» 5 матчів виграла, один програла і 2 зіграла в нічию. Який середній бал у команди «Чемпіон»?
- У літній табір дітей відправляли на 5 однакових автобусах, у яких розмістилось 29, 32, 36, 35, 31 чоловік. Чи можна було б розмістити дітей у автобусах порівну?
- Для визначення схожості насіння посіяли 4 сотні насінин окремо одну сотню від іншої. Із першої сотні зійшло 90 насінин, з другої – 92, з третьої – 87, з четвертої – 91. Визнач середню схожість насіння.
- Пробний вилов та зважування коропів-однорічок показали, що з 10 коропів чотири мали масу по 0,6 кг, три по 0,65 кг, два по 0,7 кг і один важив 0,8 кг. Обчисли середню вагу коропа-однорічки.
- З дослідних ділянок площею 4, 5 та 2 сотки зібрано відповідно 3,8 ц, 4,5 ц та 2,26 ц буряків. Знайди середній урожай буряків з однієї сотки.
ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач
Завдання 4.
- Розглянь розв’язування вправи 1616, стор. 259 підручника.
- Користуючись розглянутим прикладом, розв’яжи вправу 1617, стор. 259 підручника.
- Петрик купив 2 кг цукерок одного виду по 1,6 грн. за кілограм, 4 кг цукерок іншого виду по 2,05 грн. і ще 3 кг цукерок третього виду. Середня ціна куплених цукерок становила 2,2 грн. за кілограм. Скільки коштував кілограм цукерок третього виду?
- Середній вік одинадцяти футболістів команди становить 22 роки. Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став 21 рік. Скільки років футболісту, який залишив поле?
- Дмитрик розв’язав 10 задач. За кожну задачу він міг отримати від 6 до 12 балів. За перші вісім задач хлопчик отримав середню оцінку 7 балів. Скільки балів має отримати Дмитрик за кожну з решти двох задач, щоб середня кількість балів за одну задачу становила 8 балів?
- Середнє арифметичне чотирьох чисел дорівнює 2,1, а середнє арифметичне трьох інших чисел – 2,8. Знайди середнє арифметичне цих семи чисел.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Мотоцикліст пробув у дорозі 2 години. За першу годину він проїхав 35,7 км, а за другу – 27,9 км. Знайди середню швидкість мотоцикліста.
- Закінчи твердження:
- середнє арифметичне чисел 12 і 38 дорівнює…
- якщо середнє арифметичне двох чисел дорівнює 12, то сума чисел дорівнює …
- якщо сума трьох чисел дорівнює 27, то середнє арифметичне цих чисел дорівнює…
- Знайди середнє арифметичне чисел: 41,4; 42; 43,6; 41,8.
-
Середнє арифметичне чисел 6,9 і
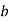 дорівнює 5,65. Знайди число
дорівнює 5,65. Знайди число 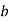 .
.
- Поїзд їхав 5 год зі швидкістю 62 км/год і 3 год зі швидкістю 52 км/год. Знайдіть середню швидкість поїзда протягом усього шляху.
- Змішали 6 кг цукерок за ціною 50,2 грн. за кілограм і 6,5 кг цукерок за ціною 80,2 грн. за кілограм. Скільки коштує 1 кг такої суміші?
Урок №17
«Не відкладайте на завтра те,
що можна зробити сьогодні»
Бенджамін Франклін
Внутрішньопредметне узагальнення матеріалу
Відсотки. Середнє арифметичне
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
Повтори тези блоку №10 і письмово дай відповіді на питання, запропоновані вчителем.
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Укажи запис у вигляді відсотків числа 0,54.
|
А |
Б |
В |
Г |
|
5,4% |
54% |
0,54% |
540% |
- Знайди 1% від 80 грн.
|
А |
Б |
В |
Г |
|
8 коп. |
80 коп. |
8 грн. |
8,8 грн. |
- Знайди середнє арифметичне чисел 6,5 і 3,5.
|
А |
Б |
В |
Г |
|
10 |
20 |
5 |
0,5 |
- У парку росте 800 дерев. Скільки дерев становлять від усіх дерев 50%?
|
А |
Б |
В |
Г |
|
8 |
80 |
400 |
20 |
Завдання 3.
Письмово виконай вправи:
- Знайди вартість тістечка, якщо 30% її становлять 1,5грн.
- Знайди середнє арифметичне чисел: 26,4; 42,6; 31,8; 15.
- Площа поля дорівнює 340га. Житом засіяли 15% поля. Скільки гектарів засіяли житом?
- Автомобіль рухався 3 год зі швидкістю 71,2 км/год і 2 год зі швидкістю 68,4 км/год. Знайди середню швидкість руху автомобіля.
- За три дні було продано 240кг овочів. Першого дня продали 25% усіх овочів, що становить 40% овочів, проданих другого дня. Скільки овочів продали третього дня?
Тема №11. Повторення матеріалу, вивченого у 5 класі
Уроки №1, 2
«Хто відплачує злом за добро,
не відступить лихе з його дому»
Книга приповістей Соломонових 17:13
Внутрішньопредметне узагальнення матеріалу
Натуральні та дробові числа
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
Усно дай відповіді на питання:
- Які числа називаються натуральними?
- Які дроби називаються звичайними?
- Які звичайні дроби – правильні, а які неправильні?
- Як додати звичайні дроби з однаковими знаменниками?
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
Знайди добуток
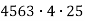 .
.
|
А |
Б |
В |
Г |
|
45630 |
4563 |
456300 |
4563000 |
-
Скільки серед дробів
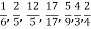 правильних?
правильних?
|
А |
Б |
В |
Г |
|
3 |
2 |
4 |
6 |
-
Виконай ділення
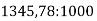 .
.
|
А |
Б |
В |
Г |
|
1345780 |
134,578 |
1,34578 |
13,4578 |
Завдання 3.
Письмово виконай вправи:
-
Знайди значення виразу:
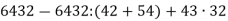 .
.
-
Обчисли:
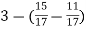 .
.
-
Обчисли, використовуючи зручний порядок дій:
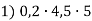 ;
; 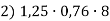 .
.
-
Знайди значення виразу:
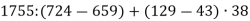 .
.
-
Виконай дії:
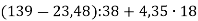 .
.
Завдання 4.
Письмово виконай вправи, стор. 263 підручника: 1661; 1672; 1693; 1704; 1723; 1728.
Уроки №3, 4
«Не той дурний, хто не знає...
але той, хто знати не хоче»
Григорій Сковорода
Внутрішньопредметне узагальнення матеріалу
Числові та буквені вирази. Формули. Рівняння
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
Усно дай відповіді на питання:
- Що називається числовим виразом?
- Як знайти значення числового виразу?
- Що таке буквений вираз?
- Що називають формулою?
- Що називають рівнянням?
- Що називають коренем рівняння?
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Письмово виконай вправи, стор. 260 підручника: 1633 (1, 3, 5); 1641 (2); 1646; 1647 (2; 4); 1649; 1677; 1679 (2).
Завдання 3.
Письмово виконай вправи, стор. 332 – 336 підручника: 1702; 1707; 1743.
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
-
Обчисли:
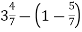 .
.
-
Знайди значення виразу:
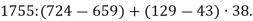 .
.
-
Розв’яжи рівняння:
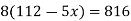 .
.
-
Знайди значення виразу
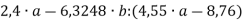 , якщо
, якщо 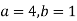 .
.
Урок №6
«Не дайте себе звести, – товариство лихе псує добрі звичаї!»
1 послання ап. Павла до коринтян 15:33
Внутрішньопредметне узагальнення матеріалу
Геометричні фігури та їх властивості. Відсотки. Середнє арифметичне
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
Усно дай відповіді на питання:
- Назви та опиши найпростіші геометричні фігури.
- Які складніші геометричні фігури ти знаєш?
- Які є види кутів і які їх кутові міри?
- Назви види трикутників за кутами та за сторонами.
- Чому дорівнює периметр многокутника?
- Чому дорівнює площа прямокутника, квадрата?
- Як обчислити об’єм прямокутного паралелепіпеда?
- Що називають відсотком?
- Як знайти відсотки від числа?
- Як знайти число за значенням його відсотків?
- Що називають середнім арифметичним кількох чисел?
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
- Тупий кут має градусну міру …
|
А |
Б |
В |
|
|
|
|
- Обчисли площу прямокутника, якщо його довжина дорівнює 3 см, а ширина – 2 см.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайди 30 % від числа 150.
|
А |
Б |
В |
Г |
|
20 |
45 |
60 |
15 |
Завдання 3.
Письмово виконай вправи:
- Одна сторона прямокутника 15 см, а друга – в 3 рази більша. Обчисли периметр і площу прямокутника.
- Морська вода містить 4 % солі. Скільки кілограм солі міститься в 320 кг морської води?
![]() K P
K P
![]() Завдання 4.
Завдання 4.
![]() Письмово виконай вправи:
Письмово виконай вправи:
N О М
-
За даним малюнком знайди градусну міру кута КОР, якщо
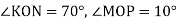 .
.
- У друкарню привезли 3860 кг паперу для друку книг. За перший день використали 35 % паперу. Скільки кілограм паперу залишилось?
Завдання 5.
Письмово виконай вправи:
- Довжина прямокутного паралелепіпеда 16 см, ширина – в 2 рази менша за довжину, а висота – на 5 см більша за ширину. Знайди об’єм паралелепіпеда.
- Змішали 3 кг цукерок за ціною 26 грн. за кілограм і 2 кг цукерок за ціною 25 грн. за кілограм. Скільки коштує 1 кг такої суміші?
![]() Готуємось до індивідуального опрацювання матеріалу
Готуємось до індивідуального опрацювання матеріалу
- Одна сторона прямокутника 18 см, а сусідня сторона на 12 см довша за неї. Обчисли периметр і площу прямокутника.
-
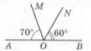 Залізна руда містить 54% заліза. Скільки тонн заліза міститься в 475 т залізної руди?
Залізна руда містить 54% заліза. Скільки тонн заліза міститься в 475 т залізної руди?
- За даним малюнком знайди градусну міру кута MON.
- На ремонт школи витратили 43 400 грн. З них 35% заплатили за роботу, а решту – за будівельні матеріали. Скільки коштували будівельні матеріали?
- Ширина прямокутного паралелепіпеда 8 дм, довжина – на 4 дм більша за ширину, а висота – у 3 рази менша від довжини. Знайди об’єм паралелепіпеда.
Урок №8
«Не відкладайте на завтра те,
що можна зробити сьогодні»
Бенджамін Франклін
Внутрішньопредметне узагальнення матеріалу за рік
І. Систематизація та узагальнення теоретичних знань
Завдання 1.
Усно дай відповіді на питання:
- Які числа називаються натуральними?
- Які дроби називаються звичайними?
- Які звичайні дроби – правильні, а які неправильні?
- Як додати звичайні дроби з однаковими знаменниками?
- Як виділити цілу частину з неправильного дробу?
- Що називається числовим виразом?
- Як знайти значення числового виразу?
- Що таке буквений вираз?
- Що називають формулою?
- Що називають рівнянням?
- Що називають коренем рівняння?
- Чому дорівнює периметр многокутника?
- Чому дорівнює площа прямокутника, квадрата?
- Як обчислити об’єм прямокутного паралелепіпеда?
ІІ. Систематизація та узагальнення практичних умінь та навичок
Завдання 2.
Усно виконай вправи:
-
З дробу
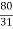 виділи цілу частину.
виділи цілу частину.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Чому дорівнює значення виразу
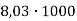 ?
?
|
А |
Б |
В |
Г |
|
803 |
8030 |
80300 |
0,803 |
- Чому дорівнює значення виразу 312,5 : 100?
|
А |
Б |
В |
Г |
|
31250 |
3,125 |
0,3125 |
0,03125 |
Завдання 3.
Письмово виконай вправи:
- Виконай дії: а) 6,132 · 5,2; б) 7,488 : 3,12.
-
Знайди значення виразу:
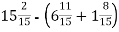 .
.
-
Розв
 яжи рівняння:
яжи рівняння: 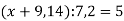 .
.
-
Знайди значення виразу:
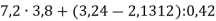 .
.
- Два мотоциклісти їхали назустріч один одному. Швидкість одного з них 24,5 км ∕ год, і вона менша від швидкості другого на 4,3 км ∕ год. Через 0,8 год вони зустрілись. Яка відстань була між ними на початку руху?
Урок №10
Міжпредметне узагальнення матеріалу
Урок – захист проектів «Ми – учні талановиті»
Клас поділений на групи в залежності від природного таланту дітей. Кожна група має певне завдання, яке необхідно підготувати, а також вміло захистити продукт своєї діяльності.
1 група
Скласти задачник, в який би входили задачі пов’язані із вашим повсякденним життям. До кожної задачі намалювати ілюстрацію. Кожен учасник групи повинен скласти хоча б 3 задачі. Далі лідер групи всі задачі збирає разом і компонує у задачник. Ваш продукт діяльності ви повинні захистити перед класом.
Приклад задачі:

В шкільну їдальню привезли овочі: 20 кг картоплі, 15 кг цибулі, а моркви половина від маси картоплі і цибулі разом. Скільки всього кілограмів овочів привезли до їдальні?
2 група:
Вам потрібно створити виставку геометричних фігур, які ми вивчали протягом року, із різноманітних матеріалів: фетр, мішковина, тканина, кольоровий папір та ін. Кожній фігурі придумати кумедне прізвисько і на захисті проекту представити ваш продукт і розповісти про кожну фігуру та її властивості. Робота колективна для всієї групи. Можна створити книжечку, в якій кожна сторінка належить одному учаснику групи.
Приклад розробки:






про публікацію авторської розробки
Додати розробку