Практична робота 8:"Табличний процесор Excel"

ПРАКТИЧНА РОБОТА № 8.

 

 Тема:   Рішення транспортних задач і задач про призначення.

 Ціль: Навчитися вирішувати транспортні задачі та задачі про призначення.

 

 

МЕТОДИЧНІ ВКАЗІВКИ.

 

8.1. Транспортна задача

 

Для рішення  транспортних задач застосовується пошук рішення. Вирішимо наступну задачу. Фірма має 4 фабрики та 5 центрів розподілу її товарів. Фабрики розташовуються в Денвері, Бостоні, Нью-Орлеані і Далласі з виробничими можливостями відповідно 200, 150, 225 й 175 одиниць продукції щодня. Розподільні центри розташовуються в Лос-Анджелесі, Далласі, Сент-Луїсі, Вашингтоні та Атланті з потребами в 100, 200, 50, 250 й 150 одиниць продукції щодня відповідно. Зберігання на фабриці не поставленої в центр розподілу одиниці продукції обходиться в $0,75 у день, а штраф за прострочення поставки замовленої споживачем у центрі розподілу одиниці продукції, але там не перебуваючої, дорівнює $2,5 у день. Вартість перевезення одиниці продукції з фабрик у пункти розподілу наведена в таблиці нижче.

 

	1	2	3	4	5	Виробництво
	Лос-Анджелес	Даллас	Сент-Луїс	Вашингтон	Атланта
Денвер	1,5	2	1,75	2,25	2,25	200
Бостон	2,5	2	1,75	1	1,5	150
Нью-Орлеан	2	1,5	1,5	1,75	1,75	225
Даллас	2	0,5	1,75	1,75	1,75	175
Потреба	100	200	50	250	150

 

Необхідно так спланувати перевезення, щоб мінімізувати сумарні транспортні витрати.

Тому що дана модель збалансована, тобто сумарний обсяг виробленої продукції дорівнює сумарному обсягу потреб, то в цій задачі не треба враховувати витрати, пов'язані як із складуванням, так і з недопоставками продукції. У противному випадку в модель треба ввести:

 

• у випадку надвиробництва - фіктивний  пункт розподілу;  вартість перевезення одиниці продукції в цей фіктивний пункт покладається вартості складування, а обсяги перевезень у цей пункт дорівнюють обсягам складування надлишок продукції на фабриках;

 

• у випадку дефіциту - фіктивну фабрику; вартість перевезень одиниці продукції з фіктивної фабрики покладається рівної вартості штрафів за недопоставку продукції, а обсяги перевезень із цієї фабрики дорівнюють обсягам недопоставок продукції в пункти розподілу.

 

Для рішення даної задачі побудуємо її математичну модель. Невідомими є обсяги перевезень. Нехай x_ij -  обсяг перевезень із i-й  фабрики в j-й центр розподілу. Функцією цілі є сумарні транспортні витрати, тобто

 

,

 

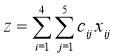де c_ij – вартість перевезення одиниці продукції з i-й  фабрики в j-й центр розподілу. Крім того, невідомі повинні задовольняти наступним обмеженням: a) ненегативність обсягу перевезень; б) тому що модель збалансована, то вся продукція повинна бути вивезена з фабрик, і потреба всіх центрів розподілу повинна бути повністю задоволена. Звідси - маємо наступну модель:

 

Мінімізувати:

,

 

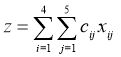при обмеженнях:

 

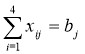, j[1,5];

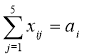, i[1,4];

, i[1,4]; j[1,5].

 

де а_i - обсяг виробництва на i-й фабриці, b_j – попит в j-м центрі розподілу.

 

Виконайте наступну підготовчу роботу для рішення задачі:

 

1. Введіть в комірки діапазону B3: F6 вартість перевезень.

2. Відведіть комірки діапазону В8:F11 під значення невідомих (обсягів перевезень).

3. Введіть в комірки діапазону Н8:H11 обсяги виробництва на фабриках.

4. Введіть в комірки діапазону B13:F13 потребу в продукції в пунктах розподілу.

5. В комірку B16 введіть функцію цілі =СУММПРОИЗВ (В3:F6; В8:F11)

6. В комірки діапазонів G8:G11 введіть формули, що обчислюють обсяги виробництва на фабриках, а в комірки діапазону B12:F12 обсяги доставляємої у пункти розподілу продукції:

 

Комірка  Формула   Комірка  Формула

 

G8   =СУММ(B8:F8)            B12   =СУММ(В8:В11)

G9   =СУММ(B9:F9)  C12   =СУММ(C8:C11)

G10   =СУММ(B10:F10) D12   =СУММ(D8:D11)

 

Комірка  Формула   Комірка  Формула

 

G11   =СУММ(B11:F11) E12   =СУММ(E8:E11)

       F12   =СУММ(F8:F11)

 

 

 

7. Виберіть команду Сервис -> Поиск решения і заповніть діалогове вікно, як показано нижче:

 

 

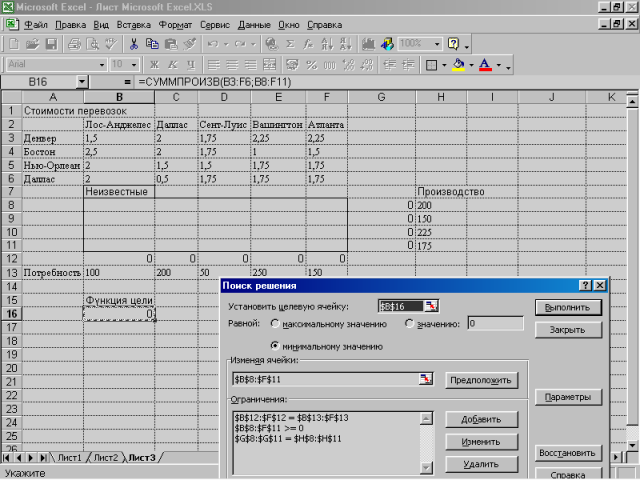
Мал. 8.1. Введення даних для вирішення транспортної задачі

HH 

8. Натисніть кнопку Выполнить. Пошук рішення знайде оптимальний план поставок продукції, а також відповідні йому транспортні витрати (мал. 8.2). На цьому транспортну задачу можна вважати вирішеною.             

 

 

 

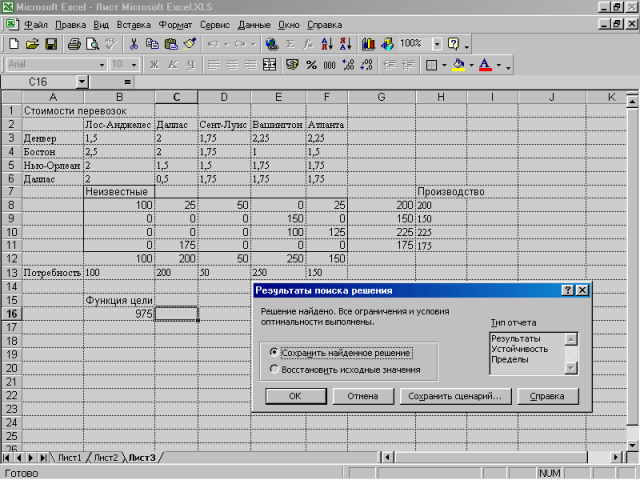
Мал. 8.2. Результати пошуку рішення транспортної задачі.

 

 

8.2. Задача про призначення

 

Розглянемо, як пошук рішення дозволяє вирішувати задачі про призначення.

У нашому випадку задача про призначення формулюється так: є чотири робітники й чотири види робіт. Вартості с_іj виконання i-м робітником j-й роботи наведені в таблиці, де під рядком розуміється робітник, а під стовпцем – робота:

 

Poб. 1	1	4	6	3
Роб. 2	9	10	7	9
Роб. 3	4	5	11	7
Роб. 4	8	7	8	5
	I вид	II вид	III вид	IV вид

Р

 

 

 

 

Необхідно так скласти план виконання робіт, щоб всі роботи були виконаними, кожен робітник був зайнятий тільки на одній роботі, а сумарна вартість виконання всіх робіт була мінімальною. Для рішення задачі спочатку побудуємо її математичну модель. Позначимо символом x_іj змінну, що має тільки два припустимих значення: 0 чи 1. Такі змінні називаються двійковими.

 

Будемо вважати, що:

 

x_іj = 1, якщо i-м робітником виконується j-я робота;

x_іj = 0, якщо i-м робітником не виконується j-я робота;

 

тобто математичну модель задачі про призначення можна сформулювати в такий спосіб: 

 

Мінімізувати:

 

,

 

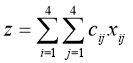при обмеженнях

 

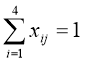, j[1,4];

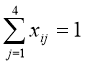, i[1,4];

, i[1,4]; j[1,4].

 

 

Для рішення задачі необхідно виконати попередні дії:

 

1. В комірки діапазону A2:D5 введіть вартості робіт.

2. Відведіть комірки діапазону F2:I5 під невідомі.

3. Введіть в комірку J1 функцію цілі, що обчислює вартість робіт

=СУММПРОИЗВ(А2:D5; F2:I5)

4.  В комірки діапазонів J2:J5 й F6:I6 введіть наступні формули, що задають ліві частини обмежень:

 

Комірка  Формула   Комірка  Формула

 

J2   =СУММ(F2:I2)     F6   =СУММ(F2:F5)

J3   =СУММ(F3:I3)  G6   =СУММ(G2:G5)

J4   =СУММ(F4:I4)  H6   =СУММ(H2:H5)

J5   =СУММ(F5:I5)  I6   =СУММ(I2:I5)

 

 

Скористаємося пошуком рішення для рішення задачі. Виберіть команду Сервис -> Поиск решения й заповніть діалогове вікно. Натисніть кнопку Выполнить. Пошук рішення знайде оптимальний план призначення на роботи (мал. 8.4).

 

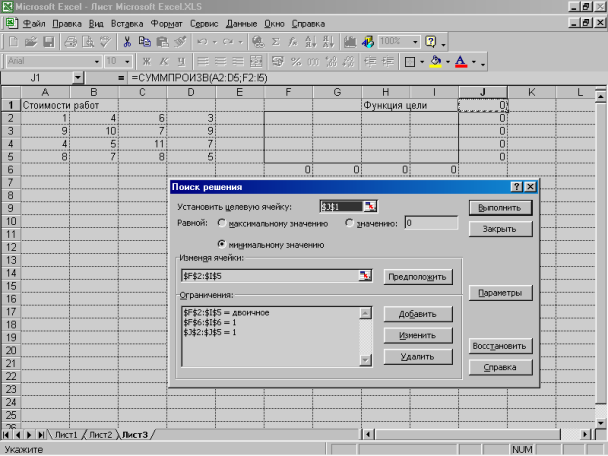
Мал. 8.3. Заповнення комірок перед пошуком рішення задачі.

 

 

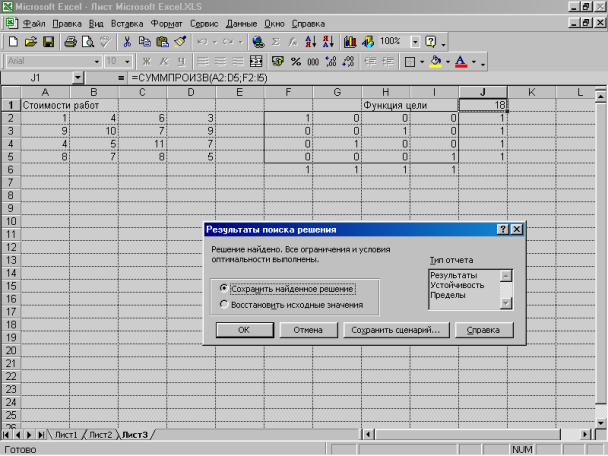
Мал. 8.4. Результати пошуку рішення задачі про призначення.

ПРАКТИЧНЕ ЗАВДАННЯ.

 

 

 8.1. Є 4 пункти виробництва і 4 пункти розподілу продукції. Вартість перевезення одиниці продукції з i-го пункту виробництва в j-й пункт розподілу с_ij наведена в таблиці, де рядок – пункт виробництва, а стовпець – пункт розподілу. В i-й рядку зазначений обсяг виробництва, а в j-м стовпці - попит у пункті розподілу. Скласти план перевезень по доставці продукції з мінімальними транспортними витратами відповідно до таблиці (де N - номер за журналом):

 

	Пункт 1.1	Пункт 2.1	Пункт 3.1	Пункт 4.1	Виробництво
Пункт 1	1	3	4	5	2N
Пункт 2	5	2	10	3	3N
Пункт 3	3	2	1	4	5N
Пункт 4	6	4	2	6	2N
Потреба	3N	2N	6N	N

 

 

8.2.  Є 3 робітників і 4 види робіт. Вартість c_ij виконання i -м робітником j-й роботи наведена в таблиці, де рядок – це робітник, а стовпець – робота. Скласти план робіт так, щоб всі роботи були виконані, кожен робітник був зайнятий тільки на одній роботі, а сумарна вартість робіт була мінімальною (N - номер за журналом):

 

 

Роб. 1	9N	4N	8N	5N
Роб. 2	1N	2N	9N	8N
Роб. 3	3N	8N	1N	9N
	I вид	II вид	III вид	IV вид

 

 

 

 

 

 

 

 

КОНТРОЛЬНІ ПИТАННЯ.

 

1. Що таке транспортна задача? У який спосіб можна її вирішити за допомогою MS Excel 2000/XP?
2. Як треба доповнити математичну модель транспортної задачі у випадку її незбалансованості?
3. Що таке задача про призначення? У який спосіб можна її вирішити за допомогою MS Excel 2000/XP?
4. У яких випадках можна ще викоритовувати засіб “Пошук рішення”?