Практичні роботи у 5 класі

ПРАКТИЧНІ РОБОТИ З МАТЕМАТИКИ

В 5-му класі

Орієнтована тематика практичних робіт

Практична робота 1

Тема. Пряма. Промінь. Відрізок.

Робота невелика за обсягом, виконується учнями в робочих зошитах.

1. Побудувати пряму а.

2. Побудувати промінь ОМ.

3. Побудувати відрізок ВС.

4. Записати зображені на малюнку прямі, відрізки та промені.

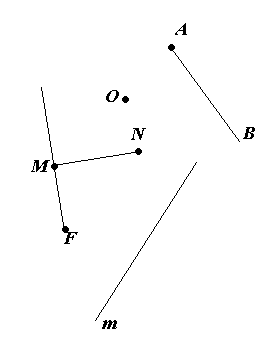
5. Чи перетинаються зображені на малюнку:

а) промінь АВ і пряма т;

б) відрізок MN і промінь АВ;

в) промінь FM і пряма ОА?

Практична робота 2

Тема. Кут.

Робота виконується на альбомних аркушах, поділених на 4 частини, і проводиться в три етапи.

Перший етап проводиться безпосередньо після пояснення та закріплення теми «Кут» і містить такі завдання.

1. У першій частині альбомного аркуша:

а) побудувати два кути, один позначити трьома буквами, другий – однією і записати побудовані кути;

б) побудувати кут AOD, провести промінь ОВ і записати утворені кути.

2. У другій частині альбомного аркуша побудувати розгорнутий, прямий, гострий і тупий кути, назвати ці кути.

На другому етапі практичної роботи учні заповнюють третю і четверту частини альбомного аркушу під час виконання такого домашнього завдання.

1. У третій частині альбомного аркуша побудувати два гострих і два тупих кути. Гострі позначити однією буквою, а тупі – трьома. Назвати побудовані кути.

2. У четвертій частині альбомного аркуша побудувати гострий кут MON; провести промінь ОК так, щоб кут KON був тупим; провести промінь ОА так, щоб кут МОА був прямим.

Третій етап практичної роботи проводиться після вивчення теми «Вимірювання кутів» з метою перевірки умінь учнів вимірювати кути.

Учням необхідно виміряти всі кути, побудовані на попередніх етапах.

Після виконання цієї роботи вчитель збирає аркуші, перевіряє правильність виконання роботи та оцінює її. Роботу над помилками, допущеними в роботі, можна виконати на зворотному боці альбомного аркуша.

Для проведення наступної практичної роботи попередньо треба виготовити набір геометричних фігур, що складається з вирізаних із картону фігур.

Практична робота 3

Тема. Многокутники.

1. Серед геометричних фігур із набору найти:

а) рівносторонній трикутник;

б) тупокутний трикутник;

в) рівнобедрений прямокутний трикутник;

г) гострокутний трикутник;

ґ) рівнобедрений гострокутний трикутник;

д) прямокутний трикутник.

2. Провести діагональ чотирикутника, попередньо відшукавши його серед фігур із набору.

3. Виміряти всі кути рівнобедреного трикутника, що є в наборі.

4. Обчислити найпростішим способом периметр рівнобедреного трикутника, що є в наборі.

Практична робота 4

Тема. Площа прямокутника і трикутника.

1. Вибрати два рівні трикутники з набору фігур. Розмістити їх так, щоб одна сторона була паралельною лінії горизонту (це основа трикутника).

2. В одному з них до основи провести висоту.

3. Розрізати трикутник вздовж проведеної висоти на два трикутники.

4. Доповнити другий трикутник отриманими трикутниками до прямокутника так, щоб довжина утвореного прямокутника дорівнювала основі трикутника, а ширина – його висоті.

5. Зробити висновок щодо обчислення площі прямокутника і трикутника.

Доцільно проводити такі практичні роботи, в яких потрібно вимірювати довжини сторін многокутників, обчислювати площі фігур та їх периметри, користуючись відповідними формулами.

Практична робота 5

Тема. Площа і периметр прямокутника і трикутника.

1. Із набору геометричних фігур вибрати прямокутник, квадрат, прямокутний трикутник, тупокутний трикутник.

2. Обчислити периметри і площі вказаних фігур.

3. Назвати різні способи обчислення площі прямокутного трикутника.

4. Як зміниться площа квадрата, якщо його сторону збільшити втричі?

5. Накреслити прямокутники зі сторонами

а) 8 см і 4 см;

б) 7 см і 5 см;

в) 6 см і 3 см;

г) 10 см і 2 см.

Що модна сказати про їх периметри? Обчислити площу кожного з побудованих прямокутників. Який із них має найбільшу площу? Що це за фігура? Що можна сказати про площі прямокутника і квадрата, периметри яких одинакові?

Виготовлені власними руками речі і математичні моделі сприяють зміцненню впевненості учнів у собі, посилюють інтерес до матеріалу, що вивчається. Виготовити модель просторової фігури – непросте завдання, але спостерігаючи за тим, з яким інтересом і бажанням учні виготовляють такі моделі, учителю легко переконатися, що таку практичну роботу необхідно виконувати.

Практична робота 6

Тема. Виготовлення геометричних моделей.

1. Виготовити прямокутний паралелепіпед, що має розміри:

а) 4 см, 6 см, 10 см;

б) 3 см, 8 см, 10 см.

2. Виготовити куб, ребро якого дорівнює:

а) 6 см;

б) 8 см.

Обчислити об’єм та площу поверхні прямокутного паралелепіпеда за числовими даними учням 5-го класу досить легко. Проте виконання такого самого завдання для відповідної моделі у них викликає розгубленість. Тому доцільно провести практичну роботу на обчислення з використанням моделей, виготовлених учнями.

Практична робота 7

Тема. Обчислення площ та об’ємів тіл.

1. Виміряти довжини ребер прямокутного паралелепіпеда.

2. Обчислити площу поверхні куба.

3. Обчислити об’єм обох фігур.

4. Поділити даний прямокутний паралелепіпед на дві частини площиною, що проходить через середину одного з бічних ребер паралельно основі. Знайти об’єм і площу поверхні кожної з частин. Чи дорівнює об’єм усього паралелепіпеда сумі об’ємів його частин? Чи правильно це для площі поверхні?

У кінці навчального року можна провести узагальнюючу практичну роботу з усього геометричного матеріалу. Набори геометричних фігур після виконання всіх практичних робіт краще зібрати в учнів і зберігати в кабінеті до наступного навчального року, а в 6-му класі поповнити їх і знову використовувати.