Презентація "Числові послідовності"
Про матеріал
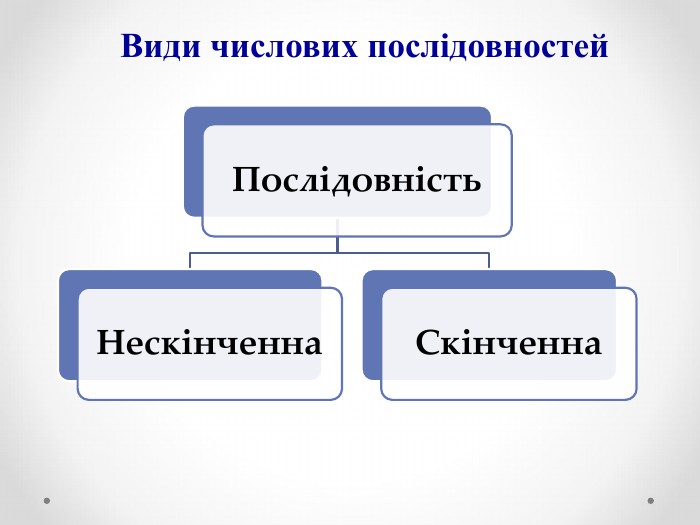
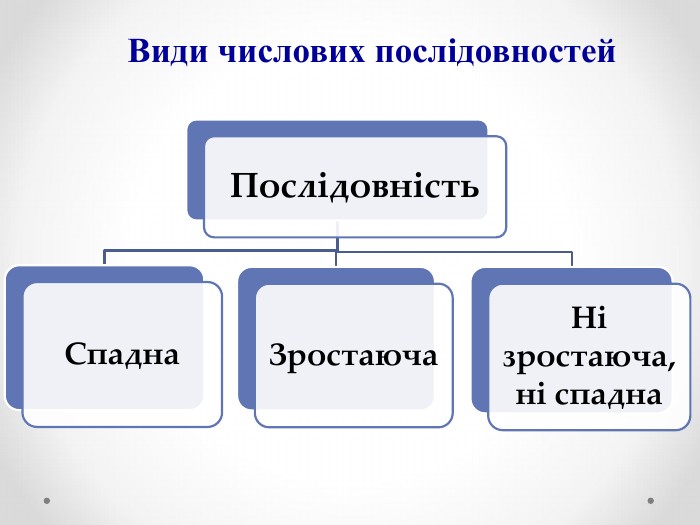
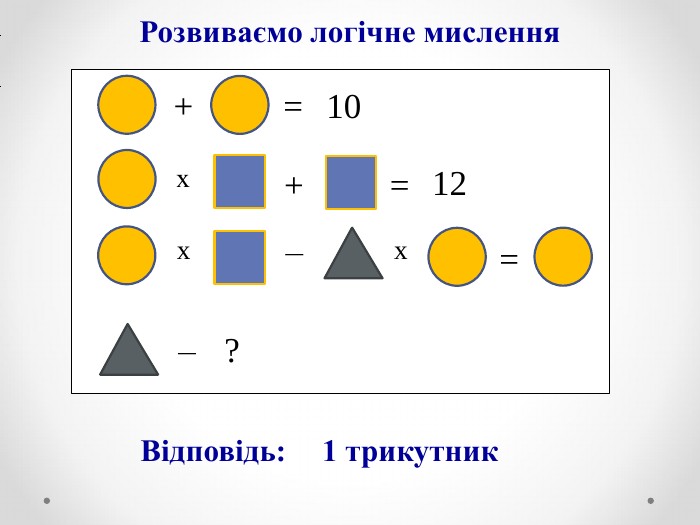
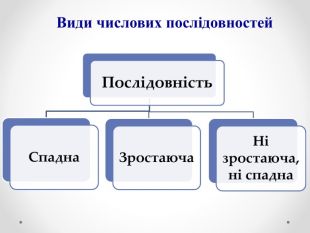
Презентація на тему «Числові послідовності» сприятиме формуванню в учнів поняття числової послідовності та формуванню вміння розв'язувати задачі, що передбачають застосування поняття числової послідовності.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку































-

Гичка Ганна
02.03.2025 в 22:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kavinska Natalija
16.02.2025 в 20:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бондаренко Тетяна Василівна
11.02.2025 в 08:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Данилець Вікторія
09.02.2025 в 15:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стельмах Оксана Анатоліївна
05.02.2025 в 22:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Щербакова Наталія Олександрівна
02.02.2025 в 18:10
Використала в роботі. Чудова презентація. Мабуть вперше нічого не редагувала "під своїх учнів". Як для нас і робилась. Щиро дякую автору.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

ПЕО комуненерго
18.04.2024 в 03:41
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука