Презентація "Деякі типи завдань, пов'язаних з функцією"
Про матеріал
Дана презентація буде корисною для вивчення теми "Функція" у 7 класі та у 8-9 класах як спосіб повторення матеріалу при підготовці до ДПА.
В презентації розібрані різні види завдань. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 7 клас (Істер О.С.)
До уроку
§ 19. Функція Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







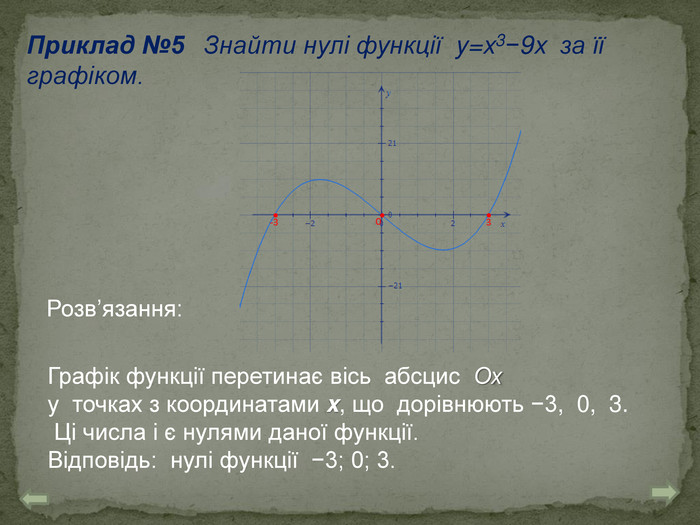




![Якщо вираз у вигляді парного кореня: треба розв’язати нерівність, де підкореневий вираз невід’ємний f(x)≥0. Відповідь D(y) обов’язково у вигляді проміжку. Якщо вираз у вигляді парного кореня у знаменнику: треба розв’язати нерівність, де підкореневий вираз додатній f(x)>0. Відповідь D(y) обов’язково у вигляді проміжку.𝑦𝑥=36−𝑥242−7𝑥 𝑦𝑥=𝑥2+3 𝑦𝑥=49−36𝑥 Якщо вираз містить декілька умов – розв’язуємо систему та знаходимо спільне рішення системи.𝑥2+3≥0, при будь якомуxR 49−36𝑥≥0,𝑥≤4936 36−𝑥2≥0,42−7𝑥>0; 𝑥∈[−6;6],𝑥<6; x [-6; 6)𝑥∈(−∞; 4936] Якщо вираз у вигляді парного кореня: треба розв’язати нерівність, де підкореневий вираз невід’ємний f(x)≥0. Відповідь D(y) обов’язково у вигляді проміжку. Якщо вираз у вигляді парного кореня у знаменнику: треба розв’язати нерівність, де підкореневий вираз додатній f(x)>0. Відповідь D(y) обов’язково у вигляді проміжку.𝑦𝑥=36−𝑥242−7𝑥 𝑦𝑥=𝑥2+3 𝑦𝑥=49−36𝑥 Якщо вираз містить декілька умов – розв’язуємо систему та знаходимо спільне рішення системи.𝑥2+3≥0, при будь якомуxR 49−36𝑥≥0,𝑥≤4936 36−𝑥2≥0,42−7𝑥>0; 𝑥∈[−6;6],𝑥<6; x [-6; 6)𝑥∈(−∞; 4936]](/uploads/files/236190/158146/170800_images/12.jpg)