Презентація ,до модуля:"Математичні основи інформатики", на тему: "Подання цілих чисел. Прямий код. Доповняльний код."
Про матеріал
Презентація ,до модуля:"Математичні основи інформатики", на тему: "Подання цілих чисел. Прямий код. Доповняльний код."
Способи представлення цілих чисел. Беззнакове подання цілого числа. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку









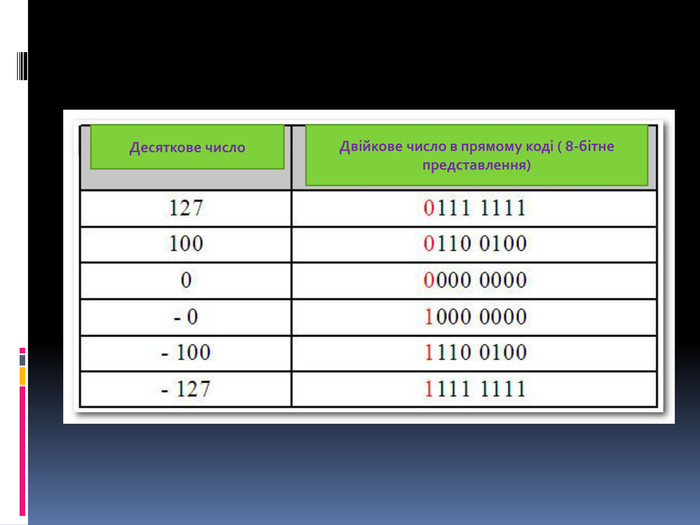
![Подання числа Подання числа в звичній для людини формі «знак-величина», при якій старший розряд комірки відводиться під знак, інші k - 1 розрядів - під цифри числа, називається прямим кодом. 2k-1 – 1 Нуль у прямому коді може бути позитивним і негативним. У прямому коді всі цифрові розряди вiд’ємного числа залишаються незмінними, а в знаковій частині записується одиниця. Приклад: A = -0,101110 [A]пр= 1,101110 Подання числа Подання числа в звичній для людини формі «знак-величина», при якій старший розряд комірки відводиться під знак, інші k - 1 розрядів - під цифри числа, називається прямим кодом. 2k-1 – 1 Нуль у прямому коді може бути позитивним і негативним. У прямому коді всі цифрові розряди вiд’ємного числа залишаються незмінними, а в знаковій частині записується одиниця. Приклад: A = -0,101110 [A]пр= 1,101110](/uploads/files/63663/118297/129651_images/9.jpg)






![Алгоритм отримання додаткового k-розрядного коду негативного числа 1. Модуль числа представити прямим кодом в k двійкових розрядах. 2. Значення всіх розрядів інвертувати (всі нулі замінити на одиниці, а одиниці - на нулі), отримавши, таким чином, k-розрядний зворотний код вихідного числа. 3. До отриманого зворотного коду, трактуемому як k-розрядний невід'ємне двійкове число, додати одиницю Приклад: A = -0,101110 [A]д = 1,010001 + 1= 1,010010 . Алгоритм отримання додаткового k-розрядного коду негативного числа 1. Модуль числа представити прямим кодом в k двійкових розрядах. 2. Значення всіх розрядів інвертувати (всі нулі замінити на одиниці, а одиниці - на нулі), отримавши, таким чином, k-розрядний зворотний код вихідного числа. 3. До отриманого зворотного коду, трактуемому як k-розрядний невід'ємне двійкове число, додати одиницю Приклад: A = -0,101110 [A]д = 1,010001 + 1= 1,010010 .](/uploads/files/63663/118297/129651_images/17.jpg)