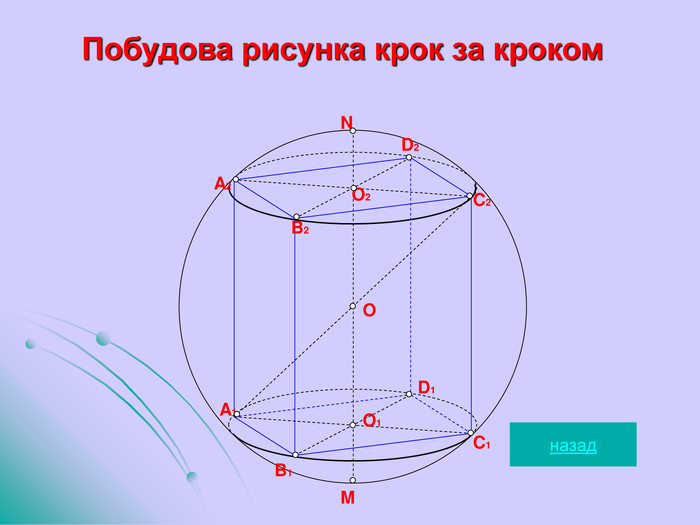
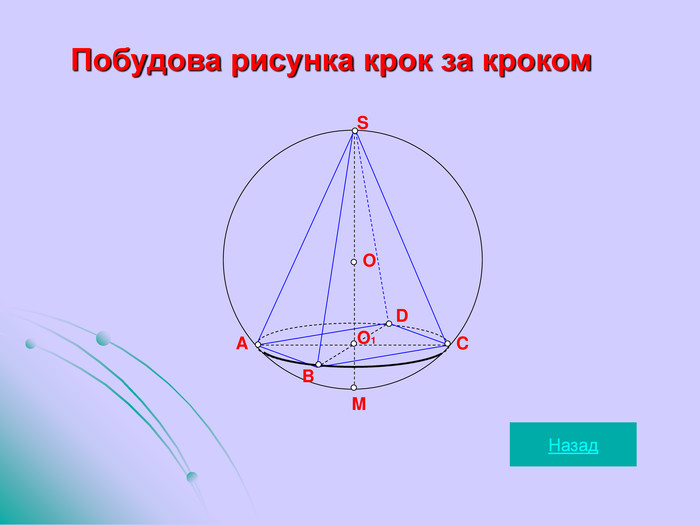
Презентація до уроку "Комбінація кулі та геометричних тіл"

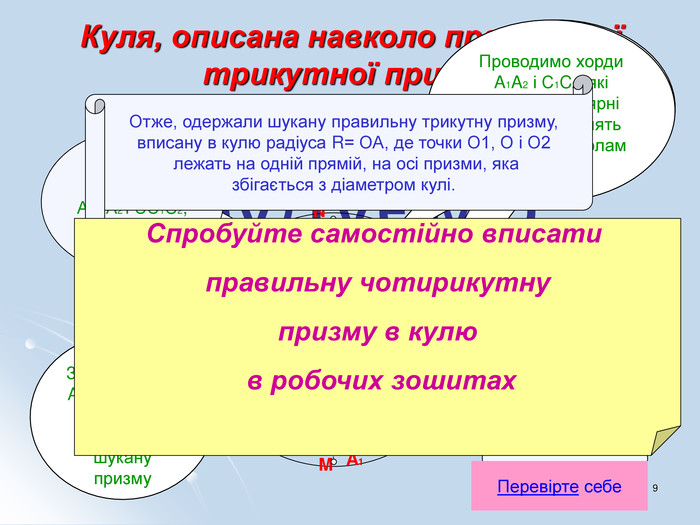
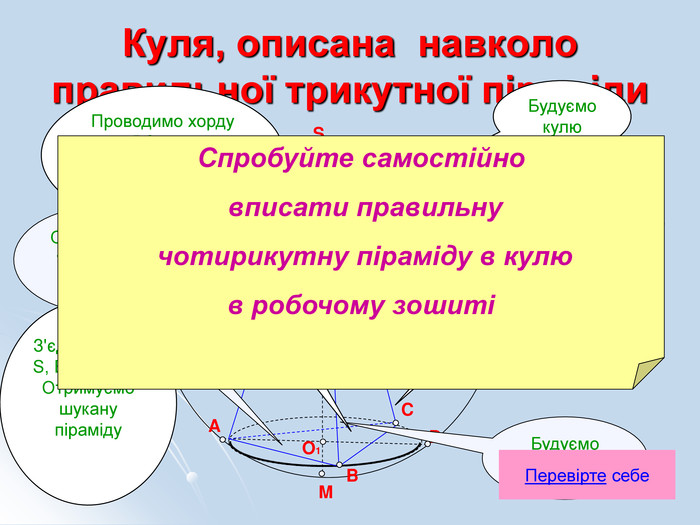
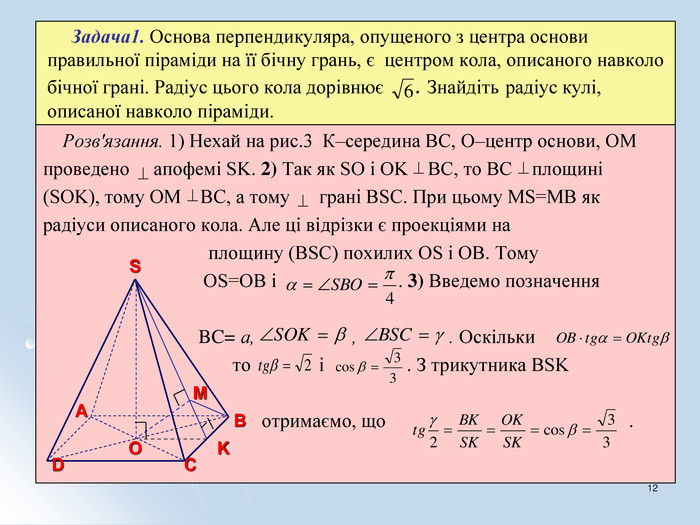
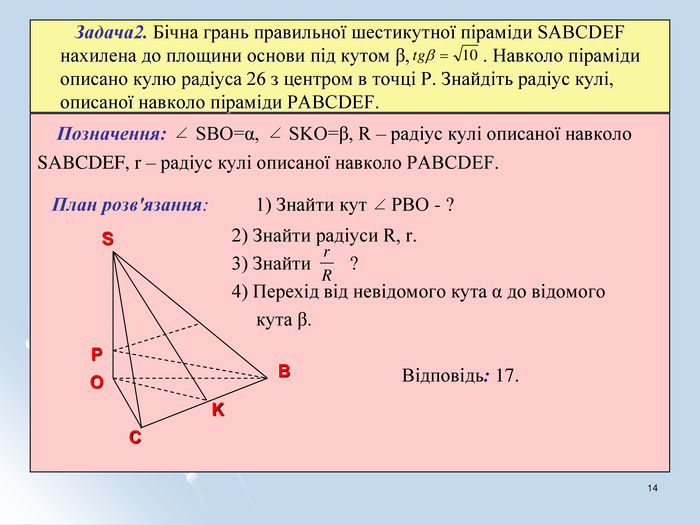
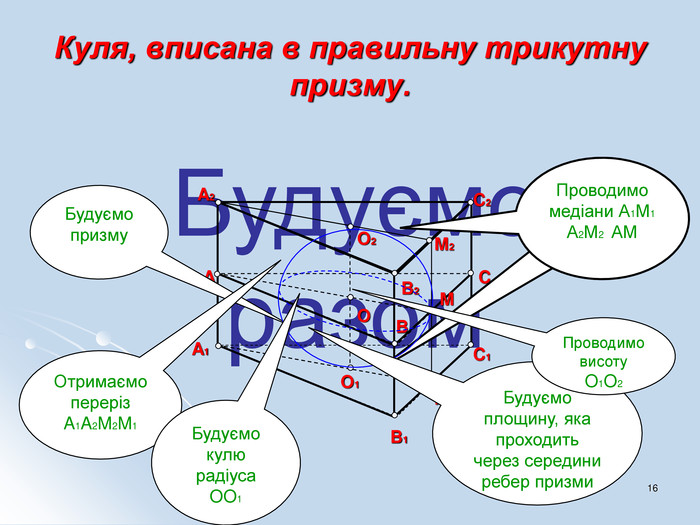
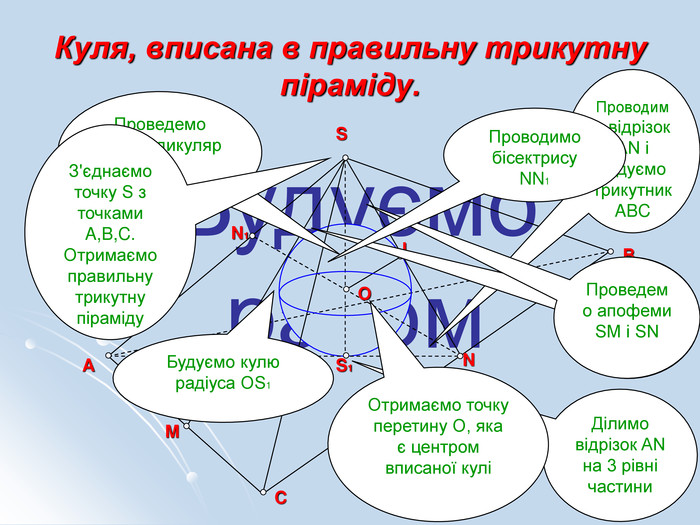
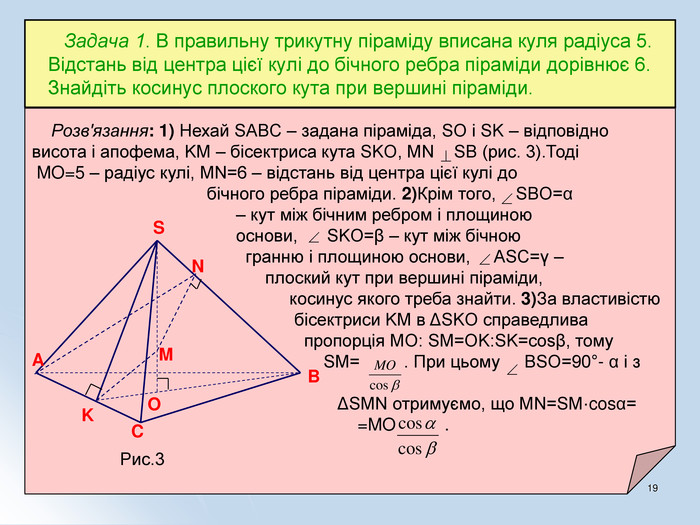
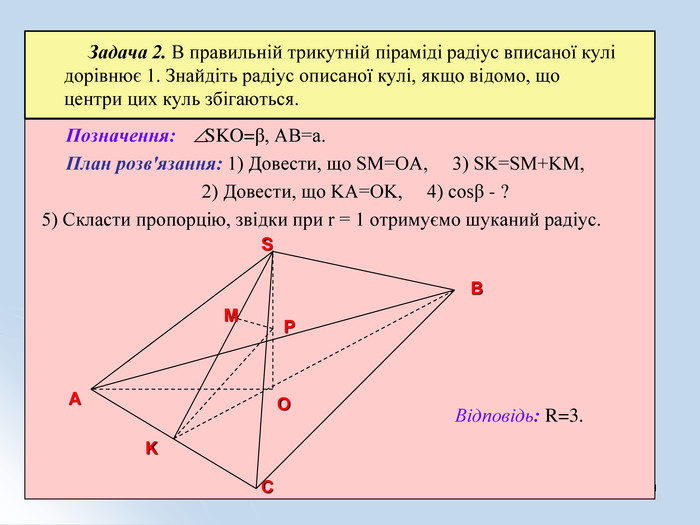
* Навчальні – формувати знання, уміння та навички розв’язування стереометричних задач на комбінації геометричних тіл та кулі. Розвивальні – розвивати творчу та пізнавальну діяльність учнів на уроці засобами розв’язування задач з аналізом даних та порівняння задач. Сприяти розвитку інтелектуальних якостей учнів таких, як самостійність та гнучкість мислення, вміння «бачити проблему», узагальнення; формувати навички колективної та самостійної роботи, вміння чітко, послідовно та аргументовано висловлюватися. Виховні - виховувати в учнів інтерес до предмету засобами використання інформаційних технологій; формувати вміння охайно та грамотно виконувати математичні записи та геометричні побудови. Вчитель Пироженко Н.А.

* До відома учнів …

Основні означення Куля називається описаною навколо многогранника, а многранник вписаним в кулю, якщо всі вершини лежать на поверхні кулі (сфери). Куля називається вписаною в многранник, а многранник описаним навколо кулі, якщо всі грані многранника дотикаються до кулі. Куля називається вписаною в циліндр, зрізаний конус (конус), якщо основи (основа) і всі твірні, які утворюють циліндр, зрізаний конус (конус), дотикаються кулі. Такий циліндр (конус) називається описаним навколо кулі. (З цього означення випливає, що в довільний осьовий переріз цих тіл можна вписати коло великого круга кулі.) Куля називається описаною навколо циліндра (зрізаного конуса), якщо основи циліндра (зрізаного конуса) є паралельними перерізами кулі. Куля називається описаною навколо конуса, якщо основа конуса є перерізом кулі, а вершина конуса лежить на поверхні кулі . Такі циліндр, зрізаний конус і конус називаються вписаними в кулю (сферу). (З цих означень випливає, що навколо довільного осьового перерізу цих тіл можна описати коло великого круга кулі.) *

* Загальні зауваження про розміщення центра кулі 1. Центр кулі, вписаної в многогранник, лежить в точці перетину бісекторних площин всіх двогранних кутів многогранника. Він розміщений тільки всередині многогранника. 2. Центр кулі, описаної навколо многогранника, лежить в точці перетину площин, які перпендикулярні до всіх ребер многогранника і проходять через їх середини. Він може бути розміщений всередині, на поверхні і поза многогранником.

* Фронтальна проекція фігур. Основні принципи фронтального косокутного проектування зводяться до наступного: а) проекція прямолінійного відрізка, паралельного площині проекцій, зберігає розміри і напрям проектованого відрізка незалежно від відстані останнього від площини проекцій; б) проекція прямолінійного відрізка, направленого перпендикулярно до площини проекцій, зображається у вигляді відрізка, направленого під кутом в 45° до прямої, прийнятої за горизонтальну, причому довжина цієї проекції зменшується удвічі порівняно з довжиною проектованого відрізка (рис.1) Рис.1 Фронтальна проекція прямокутника

* в) при зображенні круглих тіл круги, що лежать в площинах, не паралельних площині проекцій, зображаються у вигляді еліпсів. Якщо площина круга розташована горизонтально, то в геометрії велику вісь еліпса розташовують в напрямі, прийнятому на кресленні за горизонтальне. Така побудова є відступом від принципів фронтального косокутного проектування, але приймається як найпростіше та наочне зображення (рис.2) Цих трьох правил достатньо, щоб побудувати зображення довільної з просторових фігур. Рис.2 Фронтальна проекція кола До правил побудови слід приєднати ще декілька умовних правил оформлення креслення, які визначають вид ліній різного призначення.

* Висновки а) всі частини фігури, які задані в умові теореми або задачі, повинні зображатися лініями найбільшої товщини, яка підходить до розмірів рисунка; б) всі допоміжні лінії, що проводяться під час доведення теореми або розв’язування задачі, а також лінії розмірні і виносні беруться по товщині в 1/4 менші, ніж лінії основного контуру; в) осьові лінії зображаються штрихпунктиром в 1/4 товщини основної лінії; г) у просторових фігурах невидимі частини зображаються штриховими лініями; товщина їх береться удвічі менше суцільних ліній відповідного призначення; д) для зображення плоских перерізів просторових фігур використовується паралельне штрихування суцільними лініями; лінії штрихування беруться в 1/4 товщини основних ліній. В плоских фігурах для виділення деяких частин фігури також може бути використано штрихування; е) в курсі геометрії для вказівки рівності між собою двох відрізків можна перекреслювати їх однаковим числом штрихів. Рівність кутів можна відзначати перекреслюванням їх однаковим числом дуг. Такі основні правила зображення фігур в технічному кресленні, і цих же правил ми повинні строго дотримуватися і в курсі геометрії…

* Побудова зображень просторових фігур

* Будуємо разом Куля, описана навколо правильної трикутної призми Будуємо два малих круга Отримуємо трикутники АA1A2 і СC1C2, які вписані в коло C A O1 A2 M B K1 A1 O2 N C2 C1 K2 D O Перевірте себе З'єднуємо C і A, C1 і A1, С2 і A2. Отримаємо шукану призму Проводимо паралельні хорди АВ і СD Будуємо кулю Проводимо хорди A1A2 і C1C2, які перпендикулярні AB і CD та ділять О1В і О2D пополам Отже, одержали шукану правильну трикутну призму, вписану в кулю радіуса R= ОА, де точки O1, О і O2 лежать на одній прямій, на осі призми, яка збігається з діаметром кулі. Спробуйте самостійно вписати правильну чотирикутну призму в кулю в робочих зошитах

* Будуємо разом Куля, описана навколо правильної трикутної піраміди O A D C B O1 S M Будуємо малий круг Отримуємо трикутник ABC Перевірте себе Проводимо хорду АD Будуємо кулю Проводимо хорду ВС, яка перпендикулярна АD і ділить О1D пополам З'єднуємо A і S, B і S, D і S. Отримуємо шукану піраміду Спробуйте самостійно вписати правильну чотирикутну піраміду в кулю в робочому зошиті

* Висновки Теорема 2. Кулю можна описати навколо призми в тому і лише в тому випадку, якщо призма пряма і навколо її основи можна описати коло. Наслідок 1. Центр кулі, описаної навколо прямої призми, лежить на середині висоти призми, проведеної через центри кругів, описаних навколо основ. Наслідок 2. Кулю, зокрема, можна описати: навколо прямої трикутної призми, навколо правильної призми, навколо прямокутного паралелепіпеда, навколо прямої чотирикутної призми, у якої сума протилежних кутів основи рівна 180 градусів. Теорема 3. Навколо піраміди можна описати кулю в тому і лише в тому випадку, якщо навколо її основи можна описати коло. Наслідок 1. Центр кулі, описаної навколо піраміди лежить в точці перетину прямої, перпендикулярної до основи піраміди, що проходить через центр кола, описаного навколо основи, і площини, перпендикулярної будь-якому бічному ребру, проведеної через середину цього ребра. Наслідок 2. Якщо бічні ребра піраміди рівні між собою (або нахилені під одним кутом до площини основи), то навколо такої піраміди можна описати кулю. Центр цієї кулі в цьому випадку лежить в точці перетину висоти піраміди (або її продовження) з віссю симетрії бічного ребра, яка лежить в площині бічного ребра і висоти. Наслідок 3. Кулю, зокрема, можна описати: біля трикутної піраміди, біля правильної піраміди, біля чотирикутної піраміди, у якої сума протилежних кутів рівна 180 градусів. Теорема 5. Навколо будь-якої правильної зрізаної піраміди можна описати кулю (Ця умова є достатньою, але не є необхідною). Теорема 7. Навколо циліндра, зрізаного конуса, конуса можна описати кулю.

* Задача1. Основа перпендикуляра, опущеного з центра основи правильної піраміди на її бічну грань, є центром кола, описаного навколо бічної грані. Радіус цього кола дорівнює . Знайдіть радіус кулі, описаної навколо піраміди. Розв'язання. 1) Нехай на рис.3 К–середина ВС, О–центр основи, ОМ проведено апофемі SK. 2) Так як SO і OK BC, то BC площині (SOK), тому ОМ ВС, а тому грані BSC. При цьому МS=МВ як радіуси описаного кола. Але ці відрізки є проекціями на площину (BSC) похилих OS і OB. Тому OS=OB і . 3) Введемо позначення BC= а, , . Оскільки то і . З трикутника BSK отримаємо, що . A S B C O M D K

* Звідси , і радіус кола, описаного навколо бічної грані, є . 4) Тому . Центр кулі, описаної навколо піраміди, лежить на перетині OS и серединного перпендикуляра до SB, так як OS=OB, то цей перетин збігається з точкою О, а радіус описаної кулі є . Відповідь: .

* Позначення: SBO=α, SKO=β, R – радіус кулі описаної навколо SABCDEF, r – радіус кулі описаної навколо PABCDEF. План розв'язання: 1) Знайти кут PBO - ? 2) Знайти радіуси R, r. 3) Знайти ? 4) Перехід від невідомого кута α до відомого кута β. Відповідь: 17. С O P S B K Задача2. Бічна грань правильної шестикутної піраміди SABСDEF нахилена до площини основи під кутом β, . Навколо піраміди описано кулю радіуса 26 з центром в точці Р. Знайдіть радіус кулі, описаної навколо піраміди PABCDEF.

* Задача для самостоятельного решения Около сферы радиуса R описана правильная четырёхугольная пирамида, плоски угол при вершине которой равен α. Найдите площадь боковой поверхности пирамиды. Ответ: Задача для самостійного розв'язання Задача 3. Навколо сфери радіуса R описана правильна чотирикутна піраміда, плоский кут при вершині якої дорівнює α. Знайдіть площу бічної поверхні піраміди. Відповідь: .

* Будуємо разом Куля, вписана в правильну трикутну призму. A2 A1 O1 B1 M1 C1 C2 O2 O B2 B A C M2 Будуємо призму Проводимо медіани А1М1 А2М2 АМ Отримаємо переріз A1A2M2M1 Будуємо площину, яка проходить через середини ребер призми M Будуємо кулю радіуса OO1 Проводимо висоту O1O2

* Будуємо разом Куля, вписана в правильну трикутну піраміду. A C B O S N M N1 L S1 Проводимо відрізок AN і будуємо трикутник ABC Ділимо відрізок AN на 3 рівні частини Проведемо перпендикуляр SS1 З'єднаємо точку S з точками A,B,C. Отримаємо правильну трикутну піраміду Проведемо апофеми SM і SN Проводимо бісектрису NN1 Отримаємо точку перетину O, яка є центром вписаної кулі Будуємо кулю радіуса OS1

* Висновки Теорема 1. Куля можна вписати в пряму призму в тому і лише в тому випадку, якщо в основу призми можна вписати коло, а висота призми дорівнює діаметру цього кола. Наслідок 1. Центр кулі, вписаної в пряму призму, лежить на середині висоти призми, що проходить через центри кіл, вписаних в основи. Наслідок 2. Кулю, зокрема, можна вписати в прямі: трикутну, правильну, чотирикутну (у якої суми протилежних сторін основи рівні між собою) за умови Н = 2r, де Н – висота призми, r – радіус круга, вписаного в основу. Теорема 4. Якщо бічні грані піраміди нахилені під одним кутом до основи, то в таку піраміду можна вписати кулю. Наслідок 1. Центр кулі, вписаної в піраміду, у якої бічні грані нахилені під одним кутом до основи, лежить в точці перетину висоти піраміди з бісектрисою лінійного кута будь-якого двогранного кута при основі піраміди, стороною якого служить висота бічної грані, проведена з вершини піраміди. Наслідок 2. У правильну піраміду можна вписати кулю. Теорема 6. У правильну зрізану піраміду можна вписати кулю в тому і лише в тому випадку, якщо апофема піраміди рівна сумі апофем основ. Теорема 8. У циліндр (прямий круговий) можна вписати кулю в тому і лише в тому випадку, якщо циліндр рівносторонній. Теорема 9. У будь-який конус можна вписати кулю. Теорема 10. В зрізаний конус (прямий круговий) можна вписати кулю в тому і лише в тому випадку, якщо його твірна дорівнює сумі радіусів основ.

* Задача 1. В правильну трикутну піраміду вписана куля радіуса 5. Відстань від центра цієї кулі до бічного ребра піраміди дорівнює 6. Знайдіть косинус плоского кута при вершині піраміди. Розв'язання: 1) Нехай SABC – задана піраміда, SO і SK – відповідно висота і апофема, KM – бісектриса кута SKO, MN SB (рис. 3).Тоді MO=5 – радіус кулі, MN=6 – відстань від центра цієї кулі до бічного ребра піраміди. 2)Крім того, SBO=α – кут між бічним ребром і площиною основи, SKO=β – кут між бічною гранню і площиною основи, ASC=γ – плоский кут при вершині піраміди, косинус якого треба знайти. 3)За властивістю бісектриси KM в ΔSKO справедлива пропорція MO: SM=OK:SK=cosβ, тому SM= . При цьому BSO=90°- α і з ΔSMN отримуємо, що MN=SM·cosα= =MO . S B N A K C O M Рис.3

* 4) Зв'язок між тригонометричними функціями кутів α і β отримаємо так: висоту піраміди SO виражаємо двічі з трикутника SKO і трикутника SOB. З рівності враховуючи те, що OB=2·OK, знаходимо, що tgβ=2·tgα або Тому і тепер в трикутнику SKB використовуємо теорему синусів: Звідси В результаті і Відповідь: -0,28

* Позначення: SKO=β, AB=a. План розв'язання: 1) Довести, що SM=OA, 3) SK=SM+KM, 2) Довести, що KA=OK, 4) cosβ - ? 5) Скласти пропорцію, звідки при r = 1 отримуємо шуканий радіус. Відповідь: R=3. Задача 2. В правильній трикутній піраміді радіус вписаної кулі дорівнює 1. Знайдіть радіус описаної кулі, якщо відомо, що центри цих куль збігаються. С M S B P A K О

* Задача для самостійного розв'язання Задача 3. Обчислити поверхню кулі, яка вписана в трикутну піраміду, всі ребра якої дорівнюють a. Відповідь: .

* Питання 1. Знайдіть невірний вислів. Піраміда називається вписаною в конус, якщо їх висоти співпадають, а бічні ребра піраміди лежать на бічній поверхні конуса. їх вершини співпадають, і основа піраміди – многокутник, вписаний в коло основи конуса. кожне бічне ребро піраміди лежить на бічній поверхні конуса. Питання 2. Знайдіть вірне твердження. Конус називається вписаним в піраміду, якщо коло його основи вписано в многокутник, який є основою піраміди. їх висоти збігаються, а коло основи конуса вписано в многокутник, який є основою піраміди. їх вершини збігаються. Питання 3. Знайдіть невірне висловлювання. Навколо зрізаної піраміди можна описати сферу, якщо всі бічні грані зрізаної піраміди рівнобедрені трапеції. всі бічні грані зрізаної піраміди нахилені під одним кутом до площини основи. всі бічні ребра зрізаної піраміди нахилені під одним кутом до площини основи. навколо основ зрізаної піраміди можна описати кола, причому центри цих кіл лежать на висоті піраміди.

* Питання 4. Вкажіть помилкове твердження. Навколо будь - якого циліндра можна описати сферу. Навколо будь - якого конуса можна описати сферу. У  будь - який циліндр можна вписати сферу. У  будь - який конус  можна вписати сферу. Питання 5. Вкажіть помилкове речення. Циліндр називається вписаним в сферу, якщо кола його основ лежать на сфері. Зрізаний конус називається вписаним в сферу, якщо кола основ лежать на сфері. Конус називається вписаним в сферу, якщо коло його основи лежить на  сфері. Многогранник називається вписаним в сферу, якщо всі його вершини лежать на сфері. Питання 6. Вкажіть помилкове речення. У будь - яку правильну піраміду можна вписати сферу. У будь - яку трикутну піраміду можна вписати сферу.  У будь - яку чотирикутну піраміду можна вписати сферу. Якщо бічні грані піраміди нахилені під одним кутом до її основи, то в цю піраміду можна вписати сферу.

* Анкета для рефлексії учнів 1. Що нового я дізнався сьогодні на уроці? 2. Сьогодні на уроці мені сподобалося… 3. Які труднощі у мене виникли на уроці? 4. Я думаю, що ці труднощі виникли тому, що…

* Домашнє завдання 1. В правильній чотирикутній піраміді радіуси вписаної та описаної сфер дорівнюють 2 см і 5 см. Знайдіть сторону основи і висоту піраміди. (Відповідь: см, 6 см або см, 8 см.) 2. Доведіть, що якщо в правильну зрізану чотирикутну піраміду можна вписати сферу, то апофема піраміди дорівнює півсумі сторін основ її бічної грані. 3. Навколо прямої призми, основа якої є рівнобедрений трикутник зі сторонами 5 см і 6 см, описано кулю; висота призми 15 см. Знайдіть об'єм кулі. ( Відповідь: Vкулі ≈720π .)