Презентація до уроку. Тема: "Прямокутний паралелепіпед. Куб. Піраміда"
Про матеріал
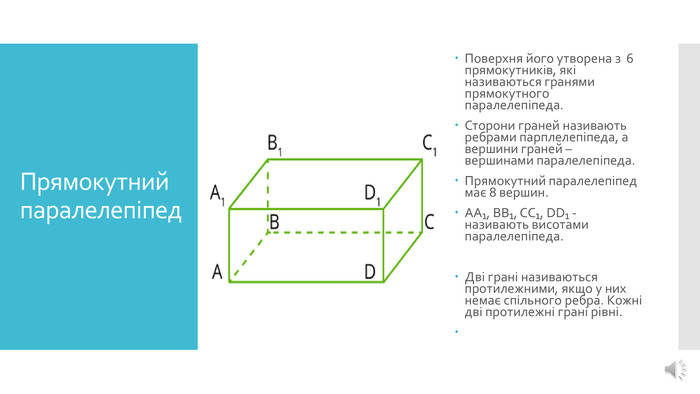
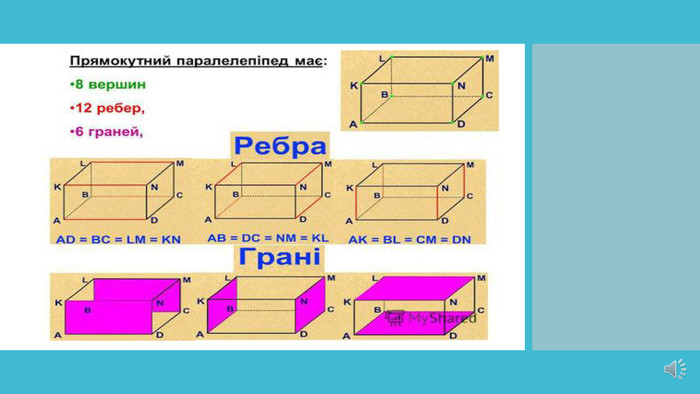
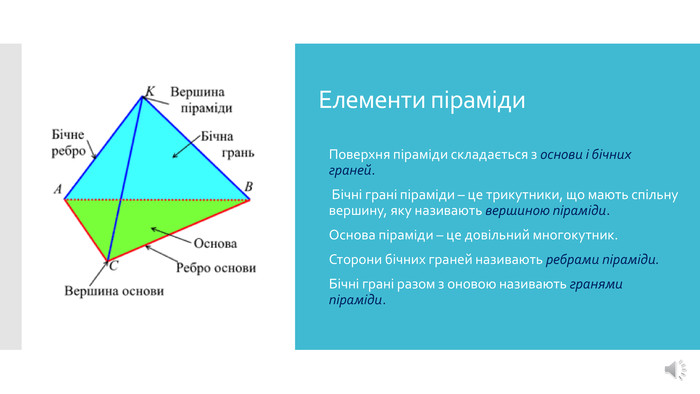
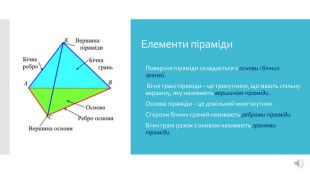
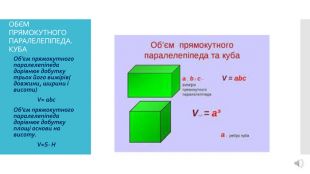
Презентація до уроку математики 5 клас. Тема: "Прямокутний паралелепіпед. Куб. Піраміда"
Мета: - дати поняття прямокутного паралелепіпеда;
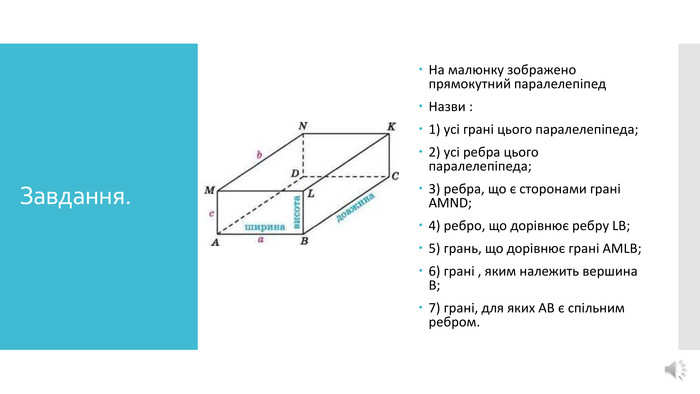
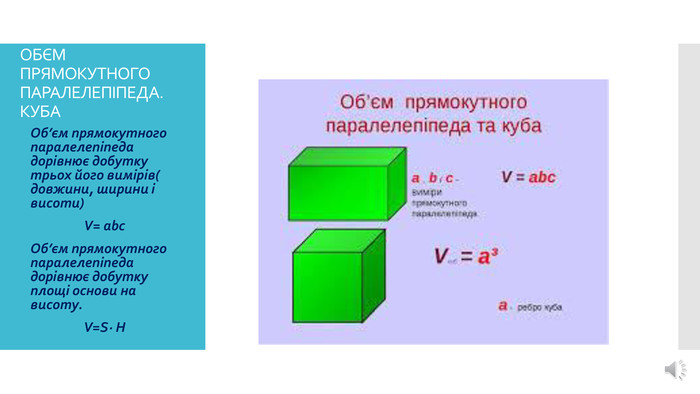
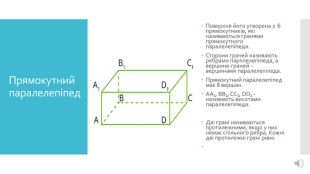
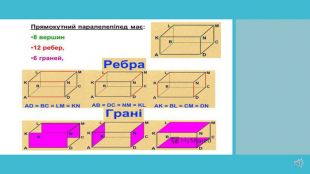
- познайомити учнів з йоговимірами, елементами;
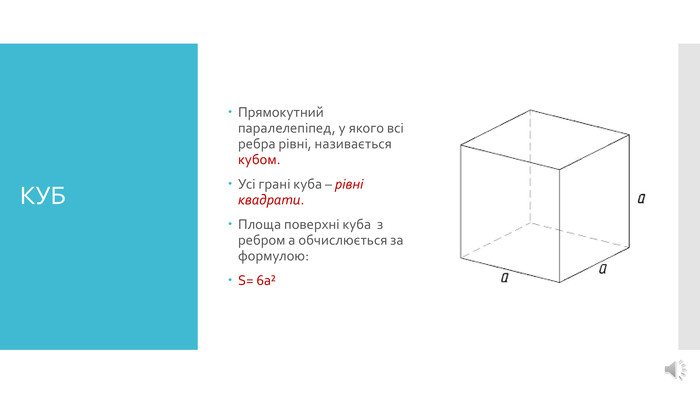
- ввести поняття про куб;
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку