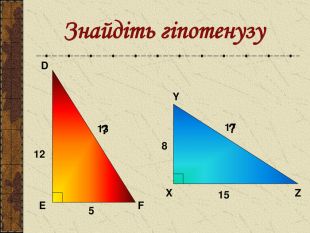
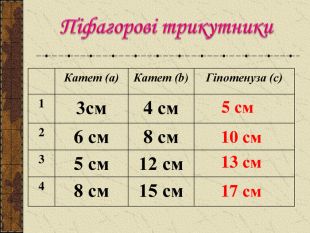
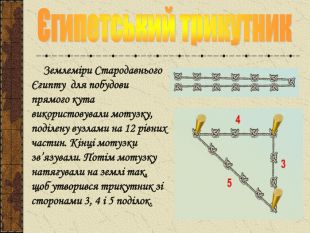
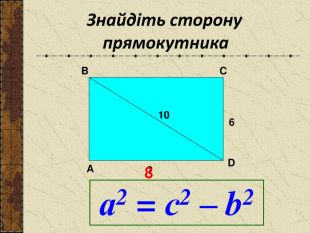
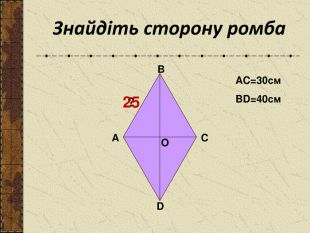
Презентація до уроку "Теорема Піфагора"
Про матеріал
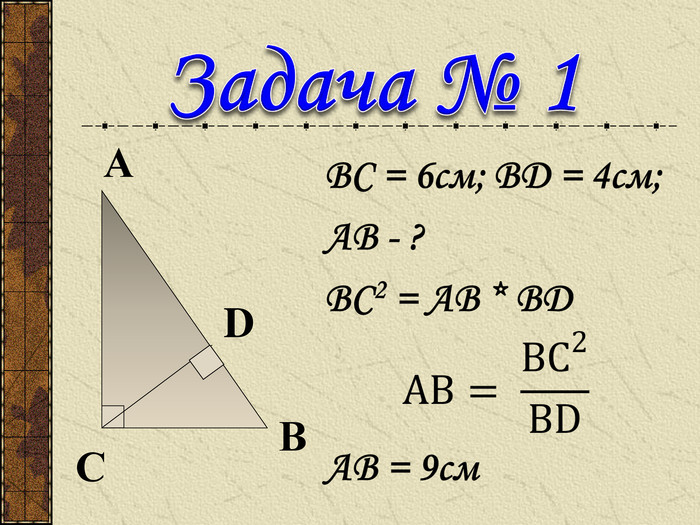
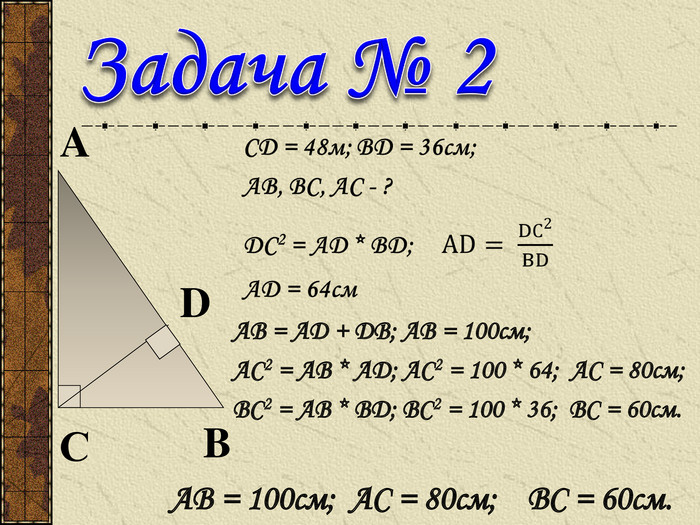
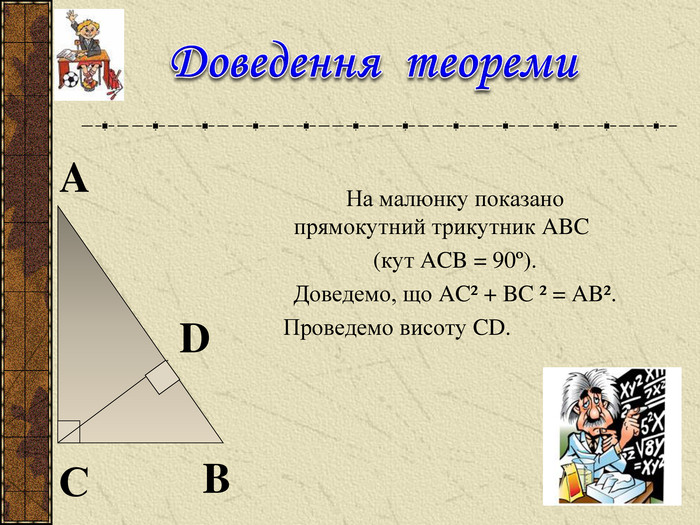
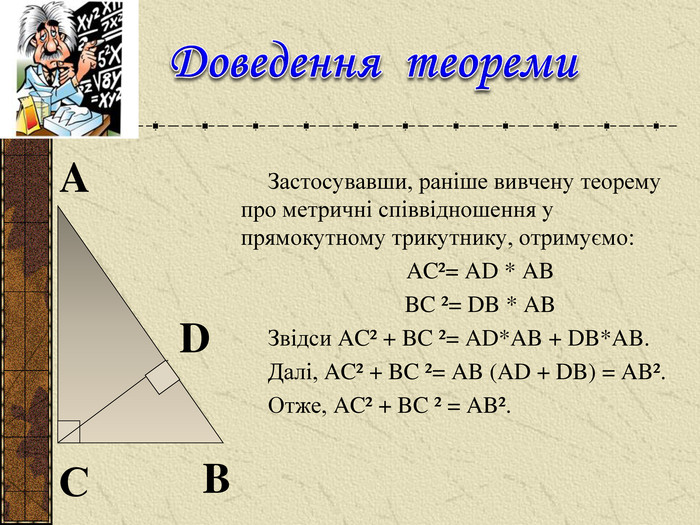
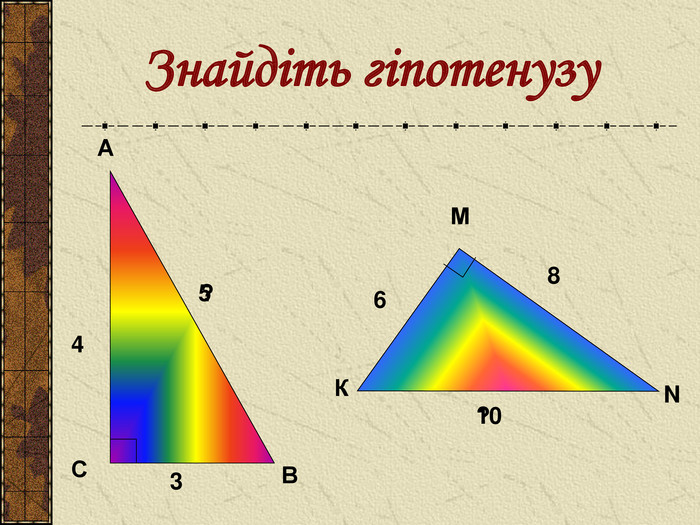
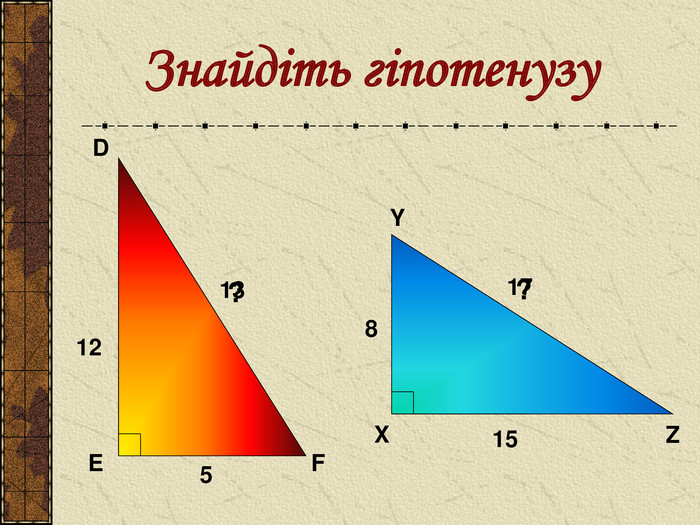
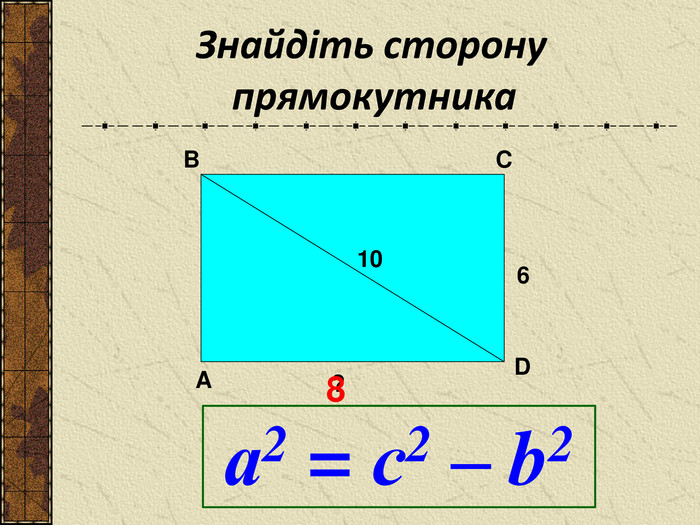
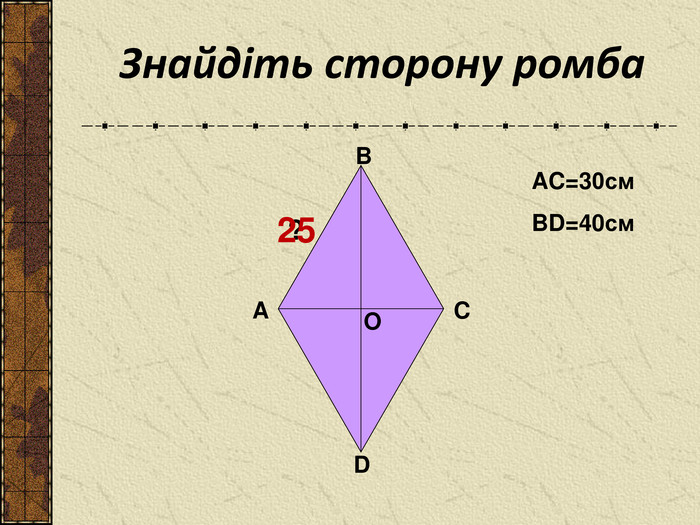
Презентація до уроку " Теорема Піфагора" допоможе цікаво і продуктивно провести вчителю цей урок. Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку