Презентація до уроку з математики "Тіла обертання. Циліндр".
Завдання поданої презентації розкрити поняття:
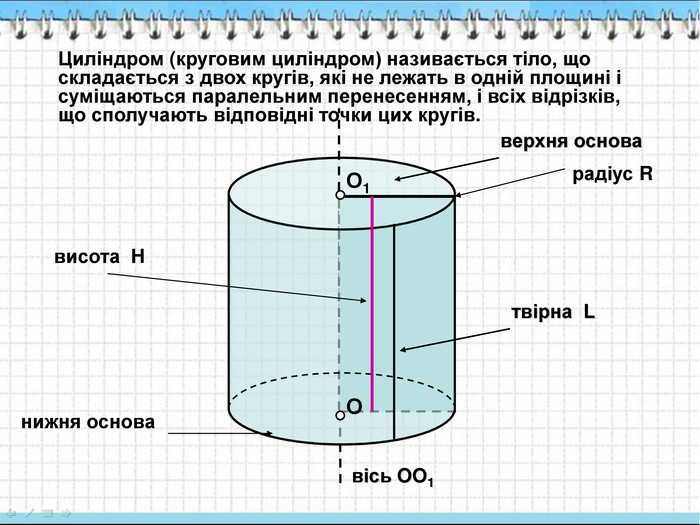
1. Циліндр, його елементи. Властивості циліндра.
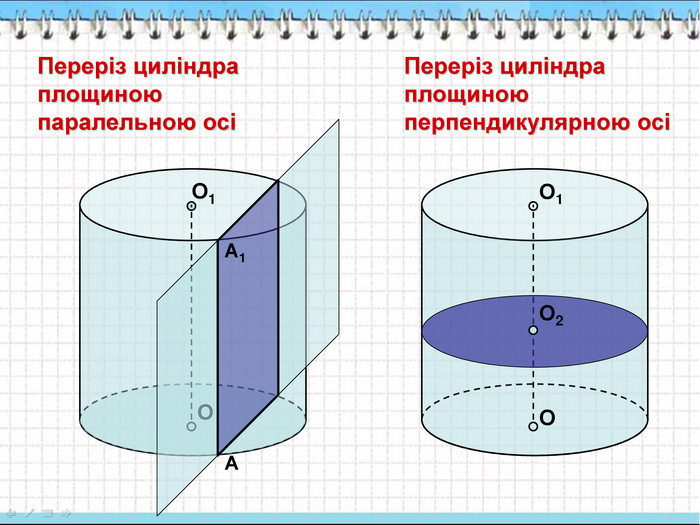
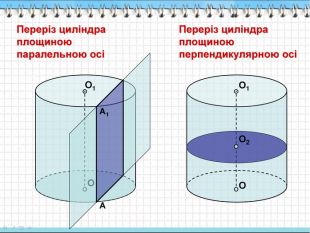
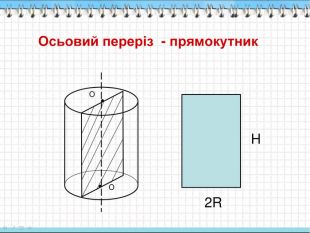
2. Перерізи циліндра.
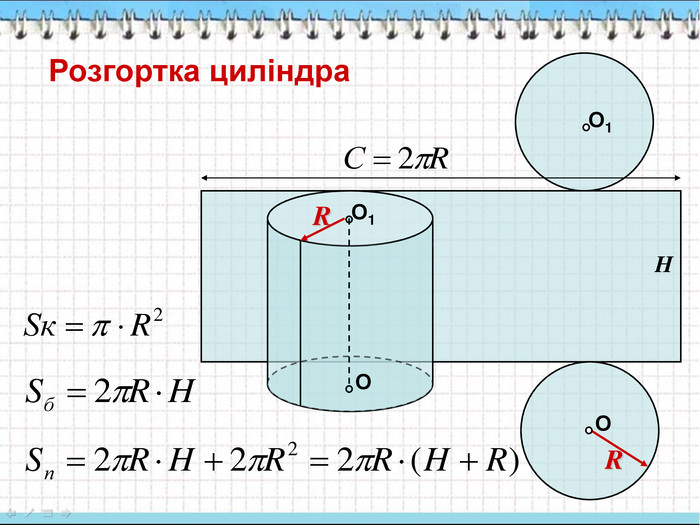
3. Бічна і повна поверхня циліндра.
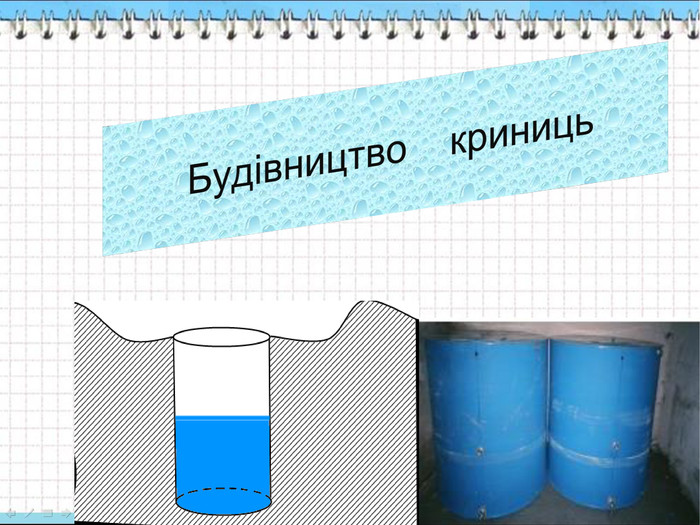
Зосередити увагу на використання циліндричних форм в житті.

























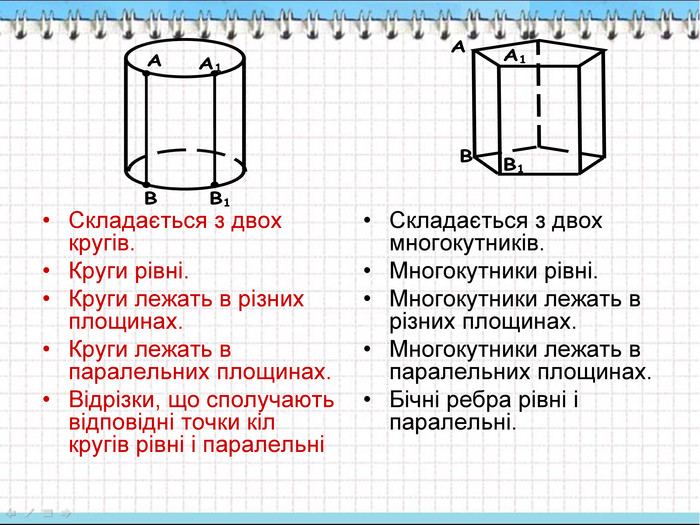
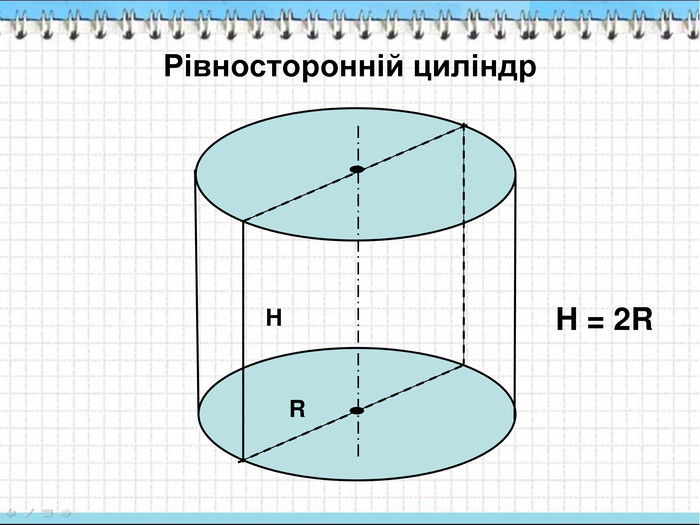
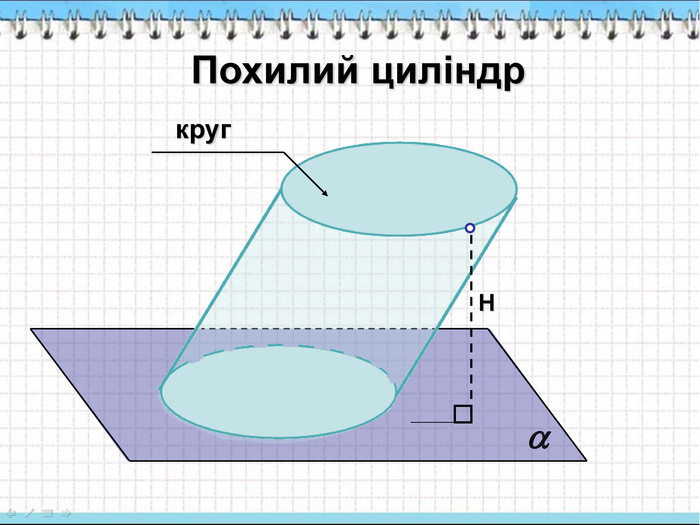










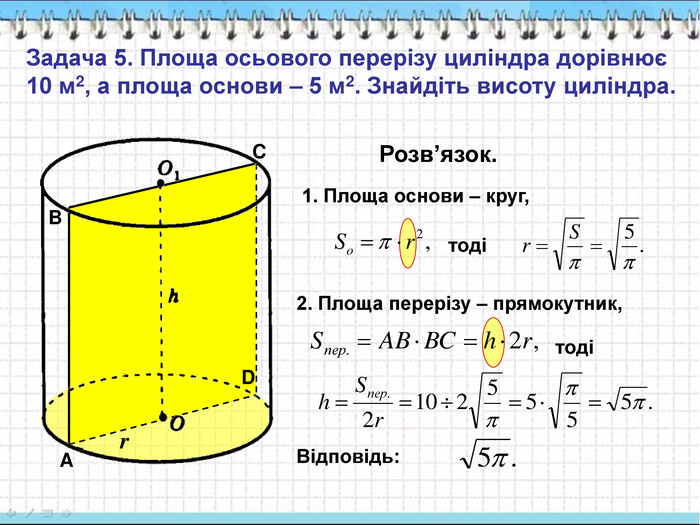

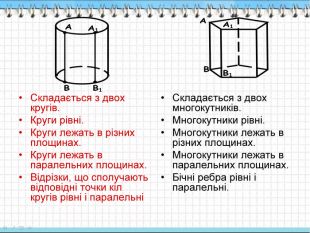
Складається з двох кругів. Круги рівні. Круги лежать в різних площинах. Круги лежать в паралельних площинах. Відрізки, що сполучають відповідні точки кіл кругів рівні і паралельні Складається з двох многокутників. Многокутники рівні. Многокутники лежать в різних площинах. Многокутники лежать в паралельних площинах. Бічні ребра рівні і паралельні.
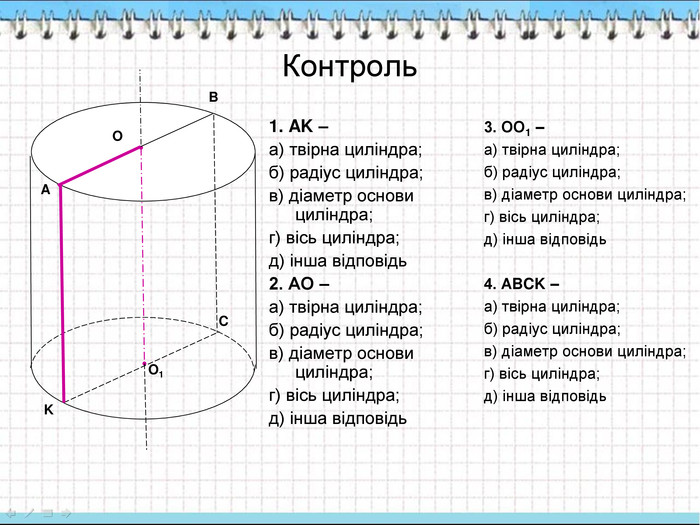
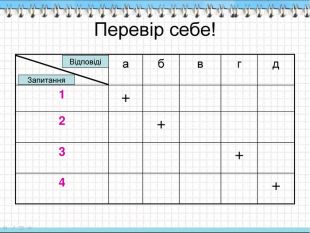
Контроль 1. AK – а) твірна циліндра; б) радіус циліндра; в) діаметр основи циліндра; г) вісь циліндра; д) інша відповідь 2. АО – а) твірна циліндра; б) радіус циліндра; в) діаметр основи циліндра; г) вісь циліндра; д) інша відповідь 3. ОО1 – а) твірна циліндра; б) радіус циліндра; в) діаметр основи циліндра; г) вісь циліндра; д) інша відповідь 4. АBCK – а) твірна циліндра; б) радіус циліндра; в) діаметр основи циліндра; г) вісь циліндра; д) інша відповідь A B C K O O1
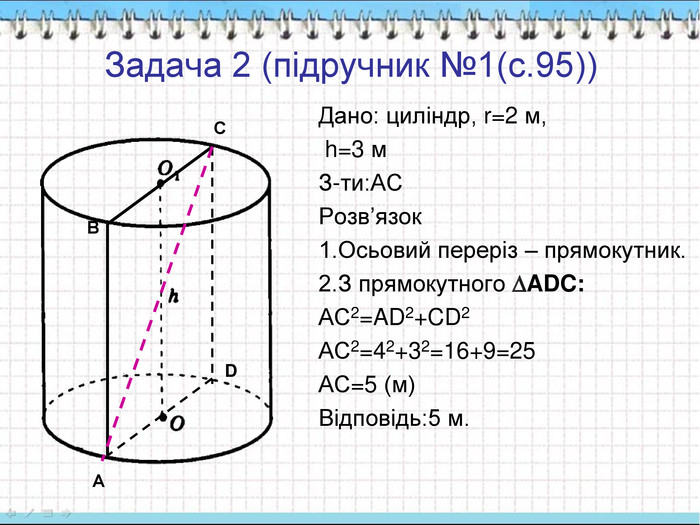
Задача 1. Знайдіть площу поверхні капелюха, розміри якого в сантиметрах зображені на рисунку. 1) Якщо дно капелюха опустити до нижніх полів, то отримаємо круг радіуса R = r1+ 10 = 20 cм. 2) Площа цього круга 3) Знайдем площу бічної поверхні циліндричної частини 4) Знайдем площу шляпи Відповідь: 600 (см2). r1=10 10 10 Розв’язок
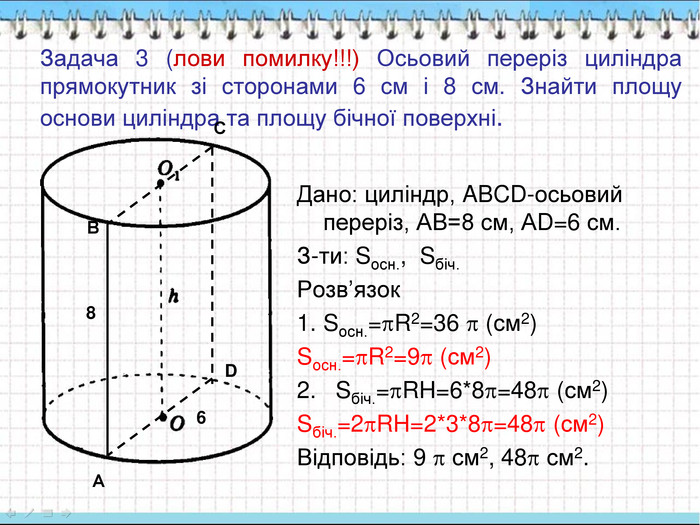
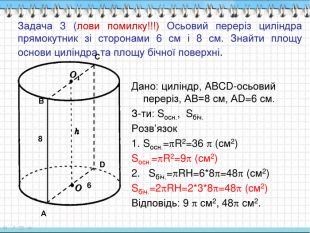
Задача 3 (лови помилку!!!) Осьовий переріз циліндра прямокутник зі сторонами 6 см і 8 см. Знайти площу основи циліндра та площу бічної поверхні. Дано: циліндр, ABCD-осьовий переріз, АВ=8 см, АD=6 см. З-ти: Sосн., Sбіч. Розв’язок Sосн.=R2=36 (см2) Sосн.=R2=9 (см2) 2. Sбіч.=RH=6*8=48 (см2) Sбіч.=2RH=2*3*8=48 (см2) Відповідь: 9 см2, 48 см2. А В С D 6 8
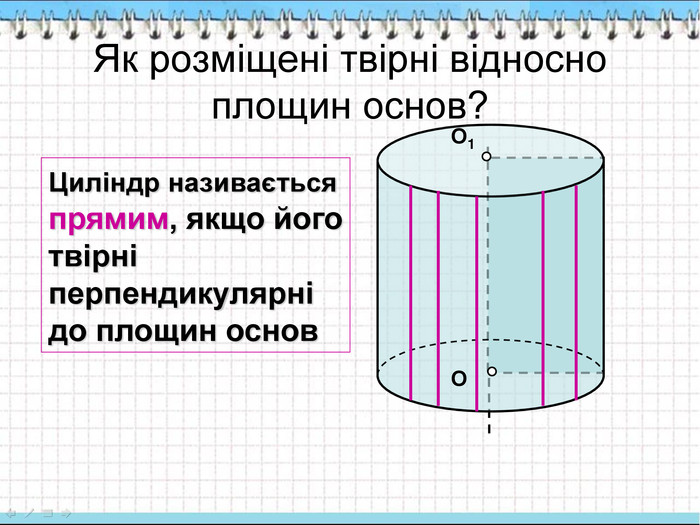
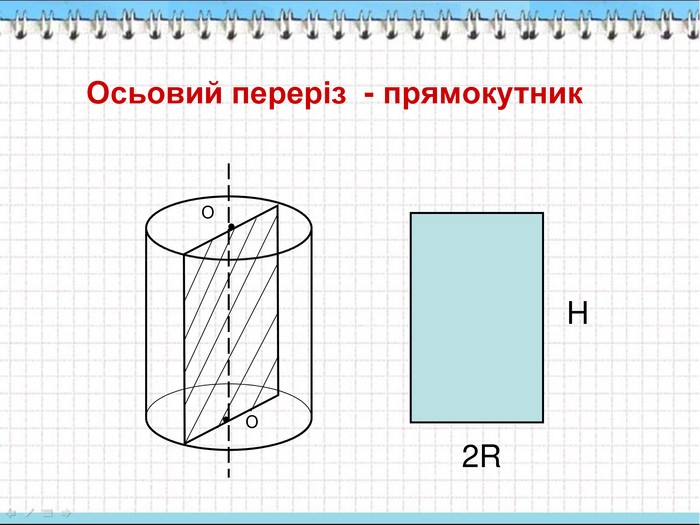
Як утворюється таке тіло обертання, як прямий круговий циліндр? Виключити елементи, які не входять в циліндр: висота, вісь, осьовий переріз, основа, апофема, квадрат, катет. Виберіть правильну відповідь: яка фігура являється осьовим перерізом циліндра? Еліпс, прямокутник, трапеція, квадрат, круг.
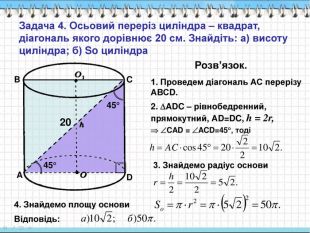
Задача 4. Осьовий переріз циліндра – квадрат, діагональ якого дорівнює 20 см. Знайдіть: а) висоту циліндра; б) So циліндра Розв’язок. 1. Проведем діагональ АС перерізу АВСD. A B C D 2. ADC – рівнобедренний, прямокутний, АD=DC, h = 2r, CAD = ACD=45, тоді 45 45 20 3. Знайдемо радіус основи 4. Знайдемо площу основи Відповідь:
Задача 6. Кінці відрізка АВ лежать на різних основах циліндра. Радіус циліндра дорівнює r, його висота – h, відстань між прямою АВ і віссю циліндра дорівнює d. Знайти: висоту, якщо r = 10, d = 8, AB = 13. r a Розв’язок. 1. Будуємо відрізок АВ. 2. Проведем радіус АО. 3. Будуємо відрізок d. А В r d К 4. Відрізок ОК – шукана відстань. 5. З прямокутного АОК знайдем: С тоді АС = 12. 6. З прямокутного АВС знайдем: Отже, h = 5. Відповідь: 5.


про публікацію авторської розробки
Додати розробку






































-

Граматна Наталія Миколаївна
14.12.2023 в 02:26
Красно дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kosyhina Elena
30.11.2022 в 09:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бершеда Людмила Олександрівна
15.11.2021 в 22:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єлькіна Світлана Володимирівна
03.11.2021 в 07:29
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Опята Людмила Іванівна
31.10.2021 в 21:36
Дуже Дякую!!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Забіла Ольга
09.11.2020 в 21:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кабанець Ольга Євгеніївна
03.11.2020 в 23:19
Дуже дякую! Відмінна презентація!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Куцобіна Жанна
01.11.2020 в 23:29
Дуже гарна робота! Дякую,Вам!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чіркова Наталя Володимирівна
31.01.2020 в 00:54
Відмінно! Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пироженко Галина
28.01.2020 в 12:51
Відмінно! Так тримати!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дятленко Надія Анатоліївна
27.10.2018 в 12:54
Ви молодець! Чудова робота! Я знаю скільки на це знадобилося і часу, і творчих зусиль. Бажаю й надалі успіхів!))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків