Урок -конференція з презентацією на тему «Задачі на знаходження найбільшого та найменшого значень фунції»

Задачі на знаходження найбільшого та найменшого значень фунцій. Урок-конференція (алгебра 11 клас)Вчитель математики Миколаївської ЗОШ №3 Прохоренко Л. В.

Тема уроку «Задачі на знаходження найбільшого та найменшого значень фунції» Ви вивчили одне із фундаментальних понять алгебри і початків аналізу – похідну. І дуже часто даєте собі запитання « А навіщо?» На попередніх уроках ви познайомились із застосуванням похідної для дослідження та побудови графіків функцій, знаходження найбільшого та найменшого значення функції на відрізку. А на сьогоднішньому уроці ви дізнаєтесь, як за допомогою похідної можна розв’язувати цікаві задачі прикладного характеру в різних сферах людської діяльності.

Компетентності1)ТЕМА: Застосування похідної до дослідження функцій.ключові- уміння вчитися; спілкуватися державною мовою, розвивати пізнавальний інтерес, навички колективної праці;галузеві- отримання та засвоєння системних знань про застосування похідної до дослідження функцій з використанням відповідного понятійного апарату. предметні - уміти застосовувати набуті знання та вміння для знаходження найбільшого та найменшого значень функції, застосування похідної до знаходження проміжків зростання і спадання функції та екстремумів функції , побудови графіків функцій та розв’язуванні задач. Компетенції з теми записані в програмі з математики для 11 класів в розділі навчальні досягнення учнів , затверджені МОН України

Наукова конференція « Будь – яка наука досягає вершин лише тоді, коли вона користується математикою» К. Маркс«Просто передати знання людині неможливо. Оволодіти ними людина може шляхом власної діяльності. « Наповнити» розум не можна, він сам повинен усе засвоїть.»А. Дістервег

План конференції Мета конференції: Навчитись розв’язувати задачі на знаходження найбільшого та найменшого значень функціїПродовжити підготовку до ЗНО1)Перевірка теоретичних знань;2)Доповідь групи « Економісти»3)Готовність до ЗНО4)Доповідь групи «Фізики»5)Готовність до ЗНО6)Доповідь групи «Архітектори»7)Підсумки конференції

Хвилинка історії математики. Хто засновник загальної теорії диференціального числення І. Ньютон чи Г. Лейбніц ? В 1708 году розгорілась сумно відома суперечка Лейбніца з Ньютоном про науковий пріоритет в відкритті диференціального числення

Суперечка між Лейбніцом та Ньютоном про науковий пріорітет стала відома як «найбільш ганебна суперечка у всій історії математики»Известно, что Лейбниц и Ньютон работали над дифференциальным исчислением параллельно и что в Лондоне Лейбниц ознакомился с некоторыми неопубликованными работами и письмами Ньютона, но пришёл к тем же результатам самостоятельно. Известно также, что Ньютон создал свою версию математического анализа, «метода флюксий» — термин Ньютона; «производная» первоначально обозначалась точкой над величиной; не позднее 1665 года, хотя и опубликовал свои результаты лишь много лет спустя; Лейбниц же первым сформулировал и опубликовал «исчисление бесконечно малых» и разработал символику, которая оказалась настолько удобной, что её используют и на сегодняшний день.

Активізація навчально-пізнавальної діяльності учасників конференціїБліц-опитування (установи відповідність)1)Функція f (x) зростає, якщо 2)Критичні точки3)Точки екстремуму4)Функція f (x) стала, якщо 5) Функція f (x) спадає, якщоа) f’ (x) =𝟎 або f’ (x) не існуєб)точки мінімуму та максимумув) f’ (x) >𝟎г) f’ (x) <𝟎д) f’ (x) =𝟎  

Підсумки наукової комісії{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1 - в2 - а3 - б4 - д5 - г

Розшифруй анаграму

Особливий інтерес представляють задачі прикладного змісту, так звані задачі на оптимізацію ,коли мова йде про дві величини, а саме потрібно знайти значення однієї, щоб інша була найбільшою , або найменшою. Від латинського «optimum» - найкращий

П. Ферма знайшов перший загальний алгоритм розв’язування задач оптимізації. Він виклав його в праці “Метод відшукання найбільших і найменших значень”Хвилинка історії математики

Задача Дідони – цариці Карфогену. Зайняти стільки землі, скільки можна вкрити шкурою вола.

Алгоритм розв’язування задач на оптимізацію. ФОРМАЛІЗАЦІЯ;РОЗВ’ЯЗУВАННЯ;ІНТЕРПРИТАЦІЯСТВОРЕННЯ МАТЕМАТИЧНОЇ МОДЕЛІ;РОЗВ’ЯЗУВАННЯ МАТЕМАТИЧНОЇ ЗАДАЧІ;АНАЛІЗ ОДЕРЖАНОГО РОЗВ’ЯЗКУ

Доповідь групи « Архітектори»

Міні-проект на тему:“Розв’язування задач прикладного характеру з використанням похідної”Група “Архітектори”

Мета проекту: Навчитися застосовувати поняття похідної для знаходження найбільшого і найменшого значення функції на відрізку; застосовувати дані знання для розв’язування прикладних задач в архітектурі; розвивати логічне мислення, вміння аналізувати і узагальнювати; виховувати любов до предмету.

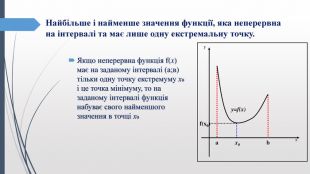
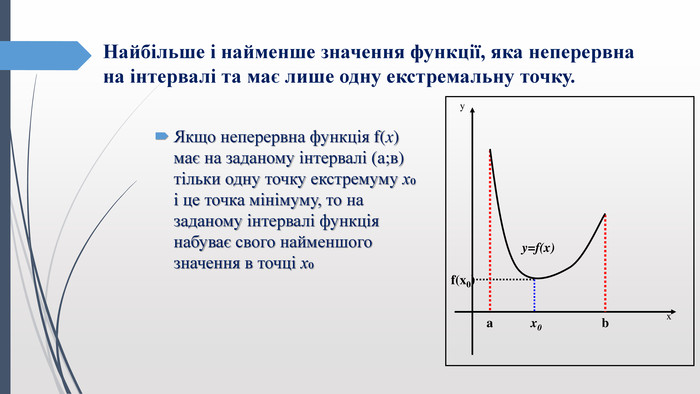
Найбільше і найменше значення функції, яка неперервна на інтервалі та має лише одну екстремальну точку. Якщо неперервна функція f(x) має на заданому інтервалі (а;в) тільки одну точку екстремуму х₀ і це точка мінімуму, то на заданому інтервалі функція набуває свого найменшого значення в точці х₀yxbax0f(x0)y=f(x)

Задача на знаходження найбільшого і найменшого значння функції

1. Одну з величин, яку потрібно знайти (або величину, за допомогою якої можна дати відповідь на запитання задачі), позначити через х ( і за змістом задачі накласти обмеження на х)

2. Величину, про яку йдеться, що вона найбільша або найменша, виразити як функцію від х.

3. Дослідити одержану функцію на найбільше або найменше значення (найчастіше за допомогою похідної)

4. Упевнитися, що одержаний результат має зміст для початкової задачі

Рецензія наукової комісіївикористання наукових методів дослідження;аргументованість висновків і обґрунтованість; вміння доповідача чітко, грамотно й аргументовано викладати матеріал, правильно оформлювати його;недоліки та зауваження щодо змістової частини роботи, оформлення.новизна постановки і розроблення проблеми;

Готуємось до ЗНО

Підсумки наукової комісіїЗНО 1 СЕСІЯ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1в2а3а

Цікаво знати. Принцип екстремуму в природі

З усіх фігур на площині, обмежених кривими лініями, найбільшу площу має круг.

З усіх прямокутників, з однаковим периметром, найбільшу площу має квадрат.

П. Ферма. Закон заломлення світла, доведений Ферма. У неоднорідному середовищі світло обирає таку траєкторію, вздовж якої час, витрачений ним на подолання шляху від однієї точки до другої, мінімальний. Хвилинка історії математики

З усіх поверхонь однакової величини найбільший об’єм має куля. Мильна плівка, набуває форму кулі, щоб вмістити найбільшу кількість задутого в неї повітря.

Доповідь групи «Фізики»

Група “Фізики”Знаходження найбільшого і найменшого значень функції, неперервної на відрізку.

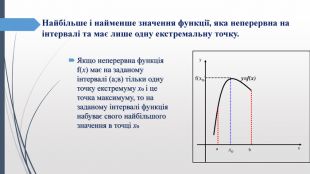
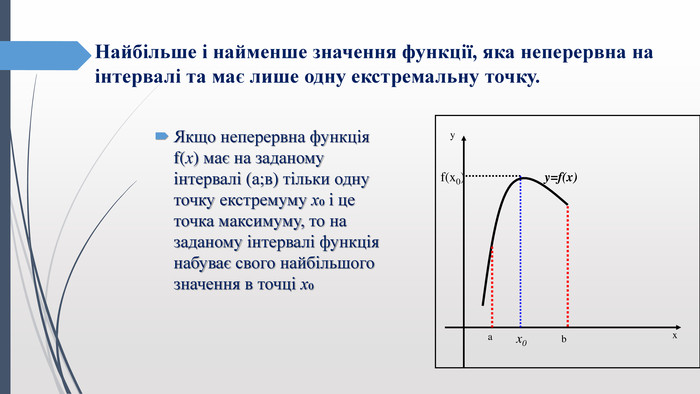
Найбільше і найменше значення функції, яка неперервна на інтервалі та має лише одну екстремальну точку. Якщо неперервна функція f(x) має на заданому інтервалі (а;в) тільки одну точку екстремуму х₀ і це точка максимуму, то на заданому інтервалі функція набуває свого найбільшого значення в точці х₀yxbax0f(x0)y=f(x)

Куля вилітає зі ствола гвинтівки вертикально вгору з початковою швидкістю 𝑣0= 800м/с. Визначити максимальну висоту підняття кулі.(g=10 м/с2 - прискорення вільного падіння)  

Розв'язання Рух тіла, кинутого вертикально вгору, здійснюється по прямій. Виберемо напрям руху осу Оу, що збігається з траєкторією руху кулі, з початком руху в точці в момент вильоту кулі зі ствола гвинтівки. З фізики відомо, що рух є рівносповільненим і висота визначається формулою: h(t) = 𝑣0t − 𝑔𝑡2/2 h = 800t - 10𝑡2/2 = 800t – 5𝑡2 Дослідимо функцію h(t) за допомогою похідної. h’(t) = 800 – 10t 

Існує для всіх t ≥0. Отже, h(t) – неперервна функція на заданому проміжку h’(t)=0 800-10t = 010t = 800t=80 – критична точка. У точці t=80, h’(t) змінює знак з плюса на мінус. Отже, t=80 – точка максимуму. Тобто, при t=80с куля підіймається на максимальну висоту. h = 800 – 10*6400/2 = 64000 – 32000 = 32000(м)

Відповідь: 32000 м h=32000 м – максимальна висота підняття вільного падіння.

Рецензія наукової комісіївикористання наукових методів дослідження;аргументованість висновків і обґрунтованість; вміння доповідача чітко, грамотно й аргументовано викладати матеріал, правильно оформлювати його;недоліки та зауваження щодо змістової частини роботи, оформлення.новизна постановки і розроблення проблеми;

Готуємось до ЗНО

Підсумки наукової комісіїЗНО 2 СЕСІЯ{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1в2д3д

Доповідь групи «Економісти»

Мета роботи : Навчитися розв’язувати задачі економічного змісту, використовуючи похідну функції

Умова задачі Необхідно виготовити відкритий резервуар циліндричної форми, об’єм якого дорівнює 64π дм3. При яких розмірах резервуару (радіуса основи та висоті) на його виготовлення витрачається найменша кількість металу?

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Назва кроку за алгоритмом. Розв’язання задачі 1. Одну з величин, яку потрібно знайти, позначити через Х Розглянемо через r (дм) — радіус основи резервуара. Оскільки об’єм циліндра V = πr2h, де h - висота, то маємо 64 π=πr2h; h=64/πr2 де r > 0 Скористаємося алгоритмом «Задачі на знаходження найбільшого і найменшого значення функції»

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}2. Величину, про яку йдеться, що вона найбільша або найменша, виразити як функцію від ХНа виготовлення ре зервуару витрачається така кількість металу S = πr2 + 2πrh, πr2 _ площа основи резервуара, 2πrh - площа бічної поверхні. Оскільки h=64/πr2 , то маємо S(r) = πr2 + 2πr(64/πr2 )

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}3. Дослідити одержану функцію на найбільше і найменше значення найменше значення функції y(r)= r2 + 128/r ) де r > 0 y*(r)= 2r – 128/r2 = (2r3 – 128)/r2 , y*(r)= 0, коли r = 4. Маємо rmin = 4

{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}4. Упевнитися, що одержаний результат має зміст для початкової задачі. Оскільки y(r)= r2 + 128/r неперервна для r > 0 і має точку мінімуму rmin = 4, то саме в цій точці і у(r), а тому і S(r) досягає найменшого значення. Отже, радіус основи циліндра дорівнює 4 дм, його висота 4дм; h=64/42 (дм).

Висновок : Ми закріпили свої навички з теми : ,,Знаходження найбільшого і найменшого значень функції, неперервної на відрізку” Побачили що всі науки пов'язанні між собою . І на окремому прикладі розв’язали задачу на економічну тематику .

Рецензія наукової комісіївикористання наукових методів дослідження;аргументованість висновків і обґрунтованість; вміння доповідача чітко, грамотно й аргументовано викладати матеріал, правильно оформлювати його;недоліки та зауваження щодо змістової частини роботи, оформлення.новизна постановки і розроблення проблеми;

Готуємось до ЗНОДодаткова сесія. АБВГД21-2-1визначити неможливо. Обчисліть тангенс кута, який утворює з додатнім напрямом осі абсцис дотична до графіка функції y=cos2x у точці з абсцисою х=Усна вправа

Підсумки наукової комісіїДОДАТКОВА СЕСІЯ

Підведення підсумків. Група «Фізики» -Група «Економісти» -Група «Архітектори» -

Підведення підсумків коференціїЩо ви чекали від уроку і що отримали?- Які етапи уроку ви вважаєте найбільш вдалими і чому?- Які події викликали яскраві враження?- Чи була користь від такого роду роботи?- В чому ви бачите власні здобутки?- Що вам найбільше вдалося під час уроку?- Які види діяльності були виконані більш вдало?- Вкажіть у порядку спадання основні проблеми і труднощі, які виникли у вас під час уроку. Якими засобами ви їх усували? « мене здивувало..». « урок дав мені для життя ..» « мені захотілося ...»МОЯ ОЦІНКА ЗА РОБОТУ

Рефлексія. Побудуйте графік результативності роботи вашої групи на уроці. Прокоментуйте вашу роботу на уроці згідно алгоритму дослідження функції

Дякую за роботу!Успіхів на ЗНО