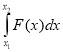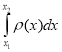Застосування визначеного інтегралу до розв’язування фізичних задач

                                                                 

 

 

 

 

 

 

 

 

 

 

 

Застосування визначеного інтегралу до розв’язування фізичних  задач

 

11 клас

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вчитель математики         

                                     Тисівської  ЗОШ  I-III ступенів

Галів В . М .  

 

 

 

 

 

         …Природа формулює свої        

                                                                             закони мовою математики

                                                                                                            Галілео Галілей

Тема уроку: Застосування визначеного інтегралу до розв’язування фізичних 

                       задач

Дидактична мета: продовжити формування навичок знаходити визначений            

                                 інтеграл, показати його місце і значення в розв’язуванні

                                 задач фізичного змісту; забезпечити єдиний підхід до

                                 ґрунтовних і цілісних знань з математики та фізики;

                                 формувати вміння застосовувати здобуті знання в

                                 нестандартних умовах; учити працювати над дослідженням і 

                                 оцінюванням фізичних явищ засобами    математики;

                                 показати значення математики в житті та   розвитку різних

                                 наук.

Розвивальна мета: сприяти розвитку творчих здібностей учнів; формувати такі 

                                 прийоми розумової діяльності як синтез, аналіз, аналогія,

                                 узагальнення, конкретизація; формувати їхній пізнавальний

                                досвід.

Виховна мета: виховувати інтерес до науки, бачення цілісності світу, вміння

                           раціонально використовувати час; намагатися створити

                           ситуацію успіху для кожного учня.

Тип уроку: інтегрований

 

Обладнання: робочі зошити, картки, мультимедійний проектор

 

ХІД УРОКУ

 

І. Організаційний етап

 

ІІ Перевірка домашнього завдання

Два учні отримують картки із завданням, подібним до завдань домашньої роботи, та розв’язують їх на дошці самостійно.

 

Картка 1

 

                     Обчисліть: ∫sin2x dx

 

Розвۥязання

 

 sin 2xdx= - cos2x =- cos π + cos 0 = 1

 

Картка 2

 

                     Розвۥязати рівняння: sin 2tdt =3 cos²x

 

 

Розвۥязання

 

-  cos 2t = ( cos 2x = 1);

 

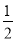• cos 2x +  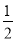 =  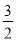cos 2x +  ;

 

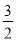cos 2x = - ;

 

2x = ± ( π-  ) + 2πn,   n  Ζ;

 

x = ± + πn,  n   Ζ.

 

ІІІ. Мотивація навчальної діяльності учнів

Учитель. Ми з вами сьогодні спробуємо за допомогою математики розв’язати проблеми, що виникають на уроці фізики. Ми з вами вже розв’язували фізичні задачі за допомогою похідної. Які задачі ми розглядали, що приводять до поняття визначеного інтеграла?

Девізом сьогоднішнього уроку ми взяли слова великого астронома Галілео Галілея :

…Природа формулює свої закони мовою математики.

Учень. А відомий французький математик Анрі Пуанкаре сказав: „Математика є спосіб називати різні речі одним імۥям“.

 

Учитель фізики. Інтеграл – це ключ , який відчиняє ворота між фізикою та математикою. Тут вони поєднуються в одне ціле. Фізика вивчає різні явища і процеси, які пов’язані зі змінними величинами, обчислювати які значно легше за допомогою визначеного інтеграла..

Учитель математики. І ви матимете чудову нагоду формувати й розвивати навички знаходження визначеного інтегралу, застосовувати його під час розв’язування практичних задач.

ІY . Актуалізація опорних знань

1. Самостійна робота ( 5 хвилин)

Варіант 1                                                                             Варіант 2

 

∫5dx = …   + C                                                                              ∫ 7dx = …   + C

 

∫…dx =    + …                                                                          ∫…dx =    + …

 

∫ cos…dx = … t + C                                                                  ∫ sin…dt =…t + C

 

∫…dx = sinx + C                                                                             ∫…dx = - cosx + C

 

 

∫…dx =   2x²    +C                                                                         ∫… dx =  8x ²  +C

 

dx = = …                                                                         x³dx = =…

Після виконання самостійної роботи відбувається самоперевірка.

Самоперевірка:

Варіант 1                                                                             Варіант 2

 

∫ 5dx = 5х  + C                                                                          ∫ 7dx =7x  + C

 

∫ х²dx =    + С                                                                       ∫ x³dx =    + C

 

∫ cos 6t dx = sin 6t + C                                                        ∫ sin 3t dt =-cos 3t + C

 

∫ cos x dx = sinx + C                                                                 ∫ sin x dx = - cosx + C

 

 

∫ 4x dx =   2x²    +C                                                                   ∫ 16 xdx =  8x ²  +C

 

dx = =                                                                    x³dx =

 

Y. Узагальнення та систематизація знань, умінь, навичок

1. Вчитель. Поняття інтеграла - важливе як у шкільному курсі математики, так і в курсі вищої математики, що розгалужується на низку складних, хоч і цікавих математичних дисциплін. Назву вам лише кілька з них:

- математичний аналіз;

- функціональний аналіз;

- теорія функцій комплексної змінної;

- теорія ймовірностей;

- теорія оптимізації математичних процесів.

Вчитель фізики. Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні. У цих науках також використовується поняття інтеграла. Серед них такі:

- електроніка;

- програмування;

- фізика;

- радіофізика.

Давайте з’ясуємо, як саме ми можемо застосувати визначений інтеграл у фізиці.

1. Фронтальне опитування

1. Наведіть приклад фізичної задачі, що привела до поняття визначеного інтеграла?

2.Охарактеризуйте фізичні величини, які зустрічаються в задачі?

3.На екрані за допомогою мультимедійного проектора відображається таблиця  1.

Вчитель. А зараз ми пограємось в карусель.

А) установіть відповідність між фізичною величиною та формулою визначеного інтеграла, за якою вона обчислюється?

 

Таблиця 1

		Величини	Знаходження похідної	Знаходження інтеграла
1	Переміщення	s –переміщення v– швидкість	v(t) = sۥ (t)	1)A=
2	Заряд	Q –електричний струм I –сила струму	I(t) = qۥ (t)	2)m=
3	Робота за прямолінійного руху	А – робота F – сила	F(x) = A ۥ(x)	3)q =I(t)dt;
4	Кількість теплоти	Q – кількість теплоти с – теплоємність	c(t) = Q ۥ(t)	4)S =v(t)dt
5	Маса	m – маса –густина	(x) = m ۥ(x)	5)Q =с(t)dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблиця 2

 

		Величини	Знаходження похідної	Знаходження інтеграла
1	Переміщення	s –переміщення v– швидкість	v(t) = sۥ (t)	4)S =v(t)dt
2	Заряд	Q –електричний струм I –сила струму	I(t) = qۥ (t)	3)q =I(t)dt;
3	Робота за прямолінійного руху	А – робота F – сила	F(x) = A ۥ(x)	1)A=
4	Кількість теплоти	Q – кількість теплоти с – теплоємність	c(t) = Q ۥ(t)	5)Q =с(t)dt
5	Маса	m – маса –густина	(x) = m ۥ(x)	3)m=

 

 

 

 

 

 

2. Розвۥязування вправ

 

1) Робота біля дошки

Задача1. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом v =2t + 1 (м/с²). Знайдіть шлях , який пройшло тіло за третю секунду руху.

Відповідь. S = 10 м.

 

 

2) Робота в групах

Клас поділяється на три групи. Кожна з груп  виконує завдання з використанням інтеграла, та  фізичних формул. Після розв’язання, правильність розв’язання задачі учні кожної групи презентують біля дошки, і визначають, який спосіб раціональніший.

 

І група

Задача 2. Обчислити роботу яку треба виконати, щоб розтягнути пружину на   0, 06 м , якщо сила 12Н розтягує іі на 0, 01 м.

Математичний метод:

За законом Гука, сила пропорційна розтягуванню або стисканню пружини, тобто F = kx, де k- величина розтягування або стискання. За умови задачі можна знайти k.

   k=, k = = 1200

Отже,  F  = 1200 х.

Звідси m(x)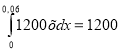

Відповідь. 2.16 Дж

Фізичний метод:

Дано:

∆ х= 0,06 м                A = ∆x                                                                                            ∆ х =0,01 м                 F = - k∆ х

  F = 12 H                         k=

                                        A =

 

ІІ група

Задача 3. Азот N масою 10 г розширюється ізотермічно при температурі -20 С, змінюючи тиск від 202 до 101 кПа. Визначіть роботу розширення.

m = 10 г = 10кг

T = -20 °C = 253 K                                      А=

p= 202 kПа = 202 000 Па                         pV=

р= 101 кПа = 101 000 Па

А-?                                                             A=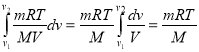lnV

 

, A=

 

 

ІІІ група.

Задача 4.З метою кращого обслуговування гонок серії „Формула-1”майстри визначили найкращий закон зміни швидкості руху автомобіля прямою трасою: v(t) = 2(t + 2).

Який шлях проїде пілот цієї гонки за 7 с від початку руху?

 

S(t)= 2 (t+2)  dt = (t+2) = (2187-8) = 1243 (м).

Відповідь. 1243 м;

 

 

YІ. Підбиття підсумків уроку

 

Експрес- опитування

 

Учитель. Що нового ти дізнався на уроці? Що вам найбільше сподобалося?

Консультанти заповнюють і здають листи оцінювання (додаються).

 

Звертаю вашу увагу на програмові вимоги та систему завдань для підготовки до незалежного зовнішнього тестування, що вміщені на ст. 273-275   з даної теми.

 

 

YІІ. Домашнє завдання

№ 4,5 ст.220

Додатково:№21 ст.274 , готуємось до ЗНО

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Лист оцінювання

Група 1

 

 

 

№ з/п	Прізвище, ім’я учня	домашнє завдання	самост. робота	усне опитув.	розв. задач	допов нення	підсу мок уроку	сума балів
1
2
3
4
5

 

 

Оцінювання

Домашнє завдання – 6-10 балів

Самостійна робота -  0-2 бали

Усне опитування -  1 бал

Розв’язування задач – 6-10 балів

Доповнення -1 бал

Підсумок уроку – 1 бал

 

Перехідна шкала оцінювання:

 

6 балів –(14-16)

7 балів – (17-19)

8 балів – (20-22)

9 балів – (23-25)

10 балів –(26-28)

11-12 балів – (більше ніж 28)