Презентація "Фрактали: математика чи інформатика"

Фрактали: математика чи інформатика?

Визначення, методи створення та типи самоподібності фракталів

Фрактал — це нерегулярна, самоподібна структура. У широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої.

Існують три поширені методи створення (генерування) фракталів: Ітераційні функції, які будуються відповідно до фіксованого правила геометричних заміщень, в результаті яких утворюються геометричні фрактали, наприклад: сніжинка Коха. Рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у кожній точці простору, фрактали отримують за допомогою нелінійних процесів в n-мірних просторах. Випадкові процеси, це фрактали, що генеруються з використанням стохастичних процесів, якщо в ітераційному процесі випадковим чином змінювати деякі параметри. Алгебраїчні фрактали. Геометричні фрактали. Стохастичні фрактали

Геометричні фракталиІтераційні функції. Сніжинка Коха. Кожного разу, коли ми додаємо один трикутник, сторона сніжинки ділиться на 4 ланки, після першого повторення ми маємо 3 Х 41 = 12, після другого ― 3 Х 42 = 48, після n-ного разу маємо 3 Х 4ⁿ. Якщо ми повторюватимемо цю дію нескінченну кількість разів, то матимемо 3 Х 4∞ = ∞, тобто нескінченну кількість сторін. Отже, периметр фігури буде нескінченним.

А як щодо площі?Намалювавши коло навколо фігури, бачимо, що вона не виходить за його межі, неважливо скільки разів ми збільшуватимемо кількість сторін. Отже, сніжинка Коха має нескінченний периметр, але обмежену площу.  Ітераційні функції. Сніжинка Коха

Розрізняють три типи самоподібності у фракталах: Точна самоподібність — це найсильніший тип самоподібності; фрактал виглядає однаково при різних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність. Майже самоподібність — слабка форма самоподібності; фрактал виглядає приблизно (але не точно) самоподібним при різних збільшеннях. Фрактали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.. Статистична самоподібність — це найслабкіша форма самоподібності; фрактал має чисельні або статистичні міри, що зберігаються при збільшенні. Ймовірнісні фрактали є прикладами фракталів, які є статистично, але не майже й не точно самоподібними.

Історичний початок та дослідження фракталів

Карл Вейерштрасс В 1872 році представив перше визначення функції з графіком що можна вважати фракталом за сьогоднішнім визначенням. Гельге фон Кох. Намалював вручну зображення, яке може тривати нескінченно, що тепер називається сніжинкою Коха. Займався вивченням ітерацій аналітичних функцій. Першим представив і вивчив множину Жуліа. Фату особливо цікавився випадком Z₀ = 0,який пізніше був проаналізований обчислювальними методами Бенуа Мандельбротом. П’єр Фату. Множина Жуліаstyle.font. Weightstyle.font. Weightstyle.font. Weight

Вперше множину Мандельброта було описано в 1905 році П'єром Фату, французьким математиком, який працював в галузі аналітичної динаміки комплексних чисел. Фату ніколи не бачив зображень, які ми зараз знаємо як зображення множини Мандельброта, тому що необхідну кількість обчислень неможливо провести вручну. Професор  Бенуа Мандельброт був першим, хто використав для цього комп'ютер. Множина Мандельброта. Множина Мандельброта

Термін фрактал був введений Бенуа Мандельбротом у 1975 році. Фрактали були описані в його книзі «Фрактальні об'єкти: форма, випадковість і розмірність». У цій книзі Мандельброт вперше використав термін «фрактал» для позначення математичного феномена, який демонструє настільки непередбачувану і дивну поведінку. Ці феномени народжувалися при використанні рекурсивного алгоритму для отримання якої-небудь кривої або множини. Множина Мандельброта — один із таких феноменів, названий за іменем свого дослідника

У 1977 році він опублікував роботу «Фрактальна геометрія природи», в якій стверджував, що випадкові на перший погляд форми є насправді складними геометричними фігурами, що складаються з менших фігур, які точно повторюють більшу.

Здається, що складні задачі потребують не менш складних розв’язань. Але іноді все виявляється зовсім навпаки. Таким чином, формула, виведена Мандельбротом має такий вигляд: Z → Z2 +C E = mc2

Бенуа Мандельброт. За допомогою відкриття Мандельброта став можливим геометричний опис предметів, що раніше не піддавалися вимірюванню — таких як хмари або малюнок рельєфу місцевості. Теорія фракталів також знайшла застосування у фізиці, хімії, астрономії, та інших галузях знання.

Фрактали і сьогодення. Практичне застосування

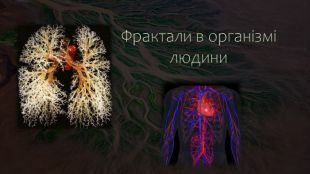
Біологія. Анатомія. За допомогою дослідження фракталів став можливим опис структури легень, таким чином математичні дослідження допомогли лікарям, що займаються дослідженням легеневих хвороб, а також захворювань печінки, де є системи з відсутністю зрозумілої геометрії.«…мені довелося створити геометрію того, що не має своєї геометрії…»Бенуа Мандельброт

Механіка рідин Фракталами добре описуються такі процеси та явища, що стосуються механіки рідин і газів: динаміка та турбулентність складних потоків;моделювання полум ‘ я; пористі матеріали, у тому числі в нафтохімії.style.opacitystyle.opacitystyle.opacity

Фрактальні антени. Фрактальна антена — це антена, в конструкції якої використані фрактальні або квазіфрактальні структури для максимізації їх ефективної довжини або збільшення периметру. Перевагами фрактальних антен є багатодіапазонність та широкосмуговість при порівняно менших розмірах. Відповідні антени виготовляють у вигляді друкованих, щілинних або дротових конструкцій

Стиснення зображень. Фрактальне стиснення зображень — це алгоритм стиснення зображень з втратами, заснований на застосуванні системи ітерованих (повторних) функцій до зображень. Даний алгоритм відомий тим, що в деяких випадках дозволяє отримати дуже високі коефіцієнти стиснення (найкращі приклади — до 1000 разів при прийнятній візуальній якості) для реальних фотографій природних об'єктів, що неможливо для інших алгоритмів стиснення зображень

Генерування фрактальних ландшафтів. Фрактальний ландшафт — це поверхня, згенерована комп'ютером з використанням стохастичного алгоритму, призначеного для створення фрактального об'єкта, який імітує зовнішній вигляд природної місцевості. Для комп'ютерного моделювання фрактального ландшафту використовується алгоритм «ромб-квадрат», за якого квадрат ділиться на чотири квадрати меншої площі, потім випадковим чином генерується карта висот, упорядкована у вигляді сітки з точок так, щоб уся площина була вкрита квадратами. Процес повторюється на чотирьох нових квадратах, і так далі, до досягнення бажаного рівня деталізації

Фрактали у природі

Фрактали в організмі людини

За фрактальними алгоритмами ростуть кристали та рослини.

Отже, відповідаючи на поставлене запитання, можна безперечно стверджувати, що фрактали ― це математика, що знайшла застосування в безлічі інших наук, що зустрічається людиною кожного дня, та точно не могла б бути повністю дослідженою без застосування комп’ютерних технологій.

Дякую за увагу!

Використані джерела:https://www.youtube.com/watch?v=WFt. Tdf3 I6 Ug&list=LL&index=44https://uk.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D1%84%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8 C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D1%82%D0%B8%D1%81%D0%BD%D0%B5%D0%BD%D0%BD%D1%8 Fhttps://sites.google.com/site/fraktalsforyou/about-fractalshttps://uchil.net/?cm=100617https://uk.wikipedia.org/wiki/%D0%9 C%D0%BD%D0%BE%D0%B6%D0%B8%D0%BD%D0%B0_%D0%9 C%D0%B0%D0%BD%D0%B4%D0%B5%D0%BB%D1%8 C%D0%B1%D1%80%D0%BE%D1%82%D0%B0https://uk.wikipedia.org/wiki/%D0%9 F%27%D1%94%D1%80_%D0%A4%D0%B0%D1%82%D1%83https://uk.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8 C%D0%BD%D0%B0_%D0%B0%D0%BD%D1%82%D0%B5%D0%BD%D0%B0https://uk.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8 C%D0%BD%D0%B8%D0%B9_%D0%BB%D0%B0%D0%BD%D0%B4%D1%88%D0%B0%D1%84%D1%82https://www.youtube.com/watch?v=ay8 OMOsf6 AQ&t=292shttps://www.youtube.com/watch?v=DHNoo. Ae44d. Y&list=LL&index=44&t=125shttps://uk.theastrologypage.com/fractal

* У презентації викорстані фрагмкнти відео з каналу. MITK12 Videos