Презентація "Комбінації геометричних тіл"
Про матеріал
Презентація "Комбінація геометричних тіл" описує усі можливі комбінації геометричних тіл.Ò
1.Многогранник і многогранник.
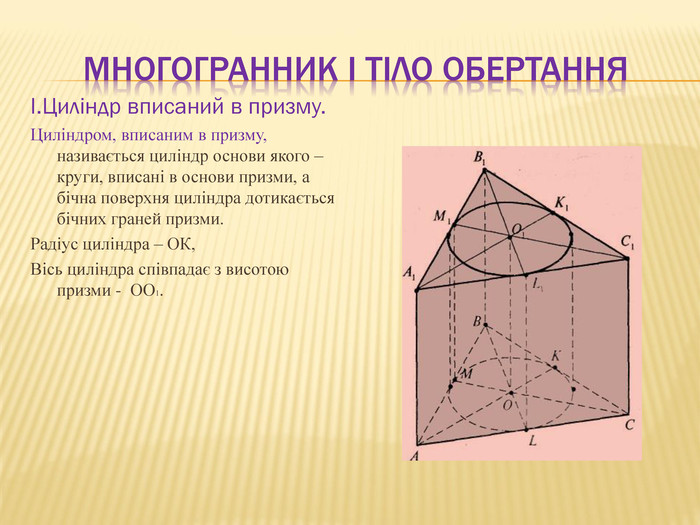
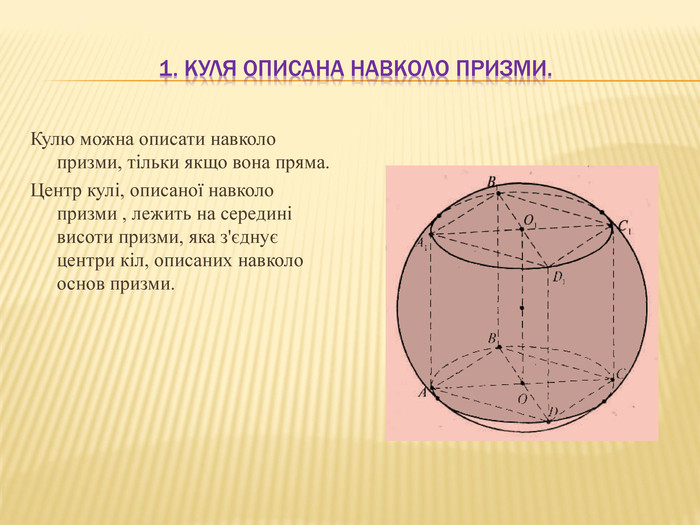
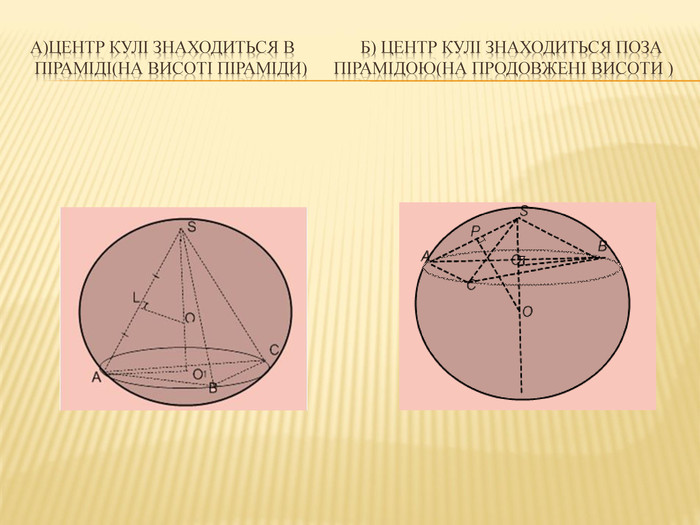
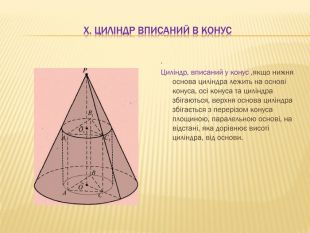
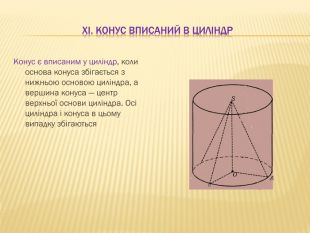
2.Многогранник і тіло обертання.
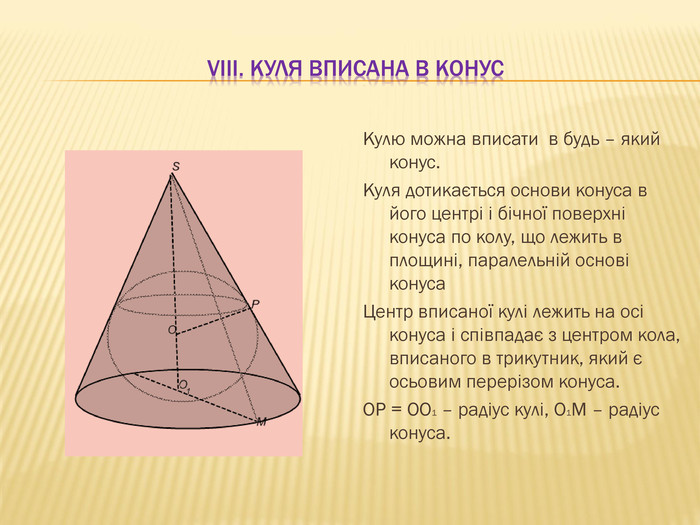
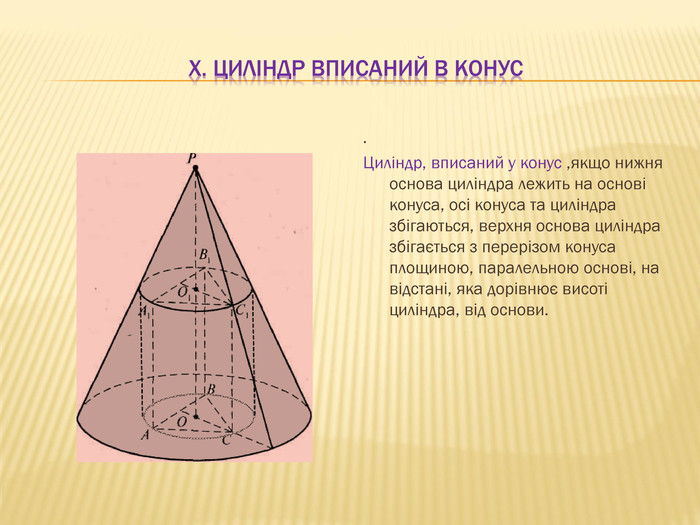
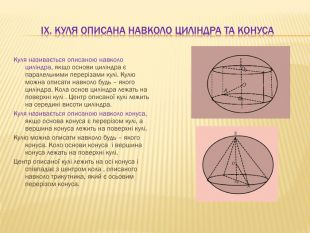
3.Тіло обертання і тіло обертання.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку