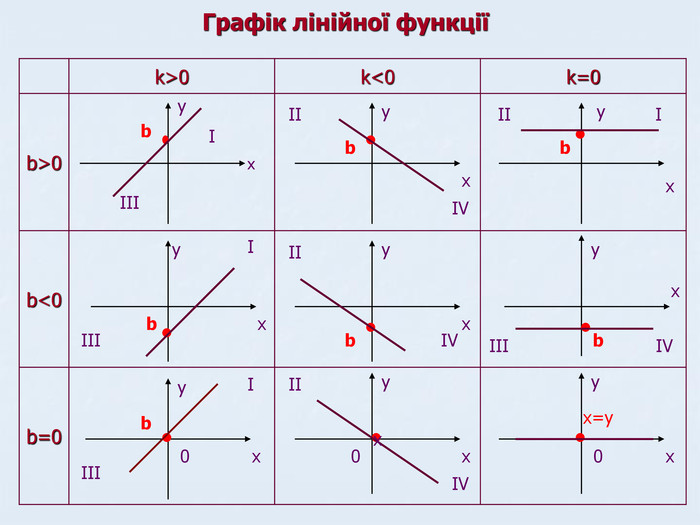
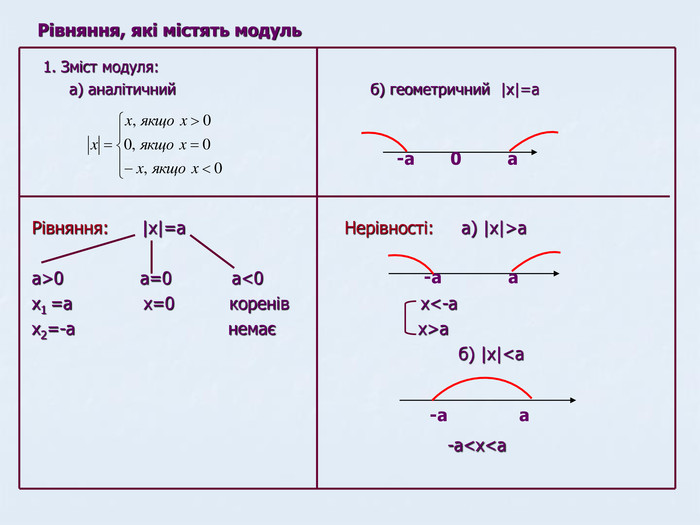
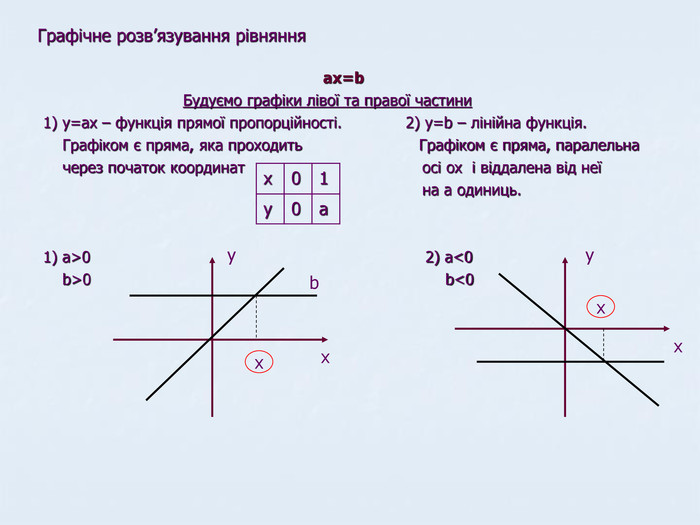
Презентація Лінійна функція
Про матеріал
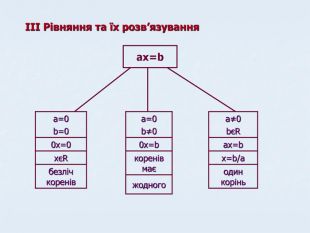
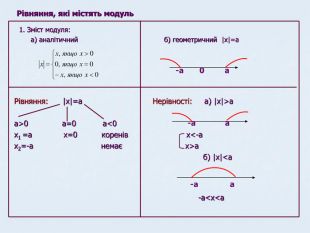
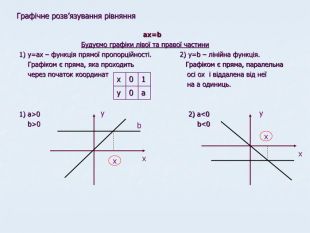
Матеріали даної презентації дають можливість систематизувати та повторити вивчене з теми"Лінійна функція" Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку