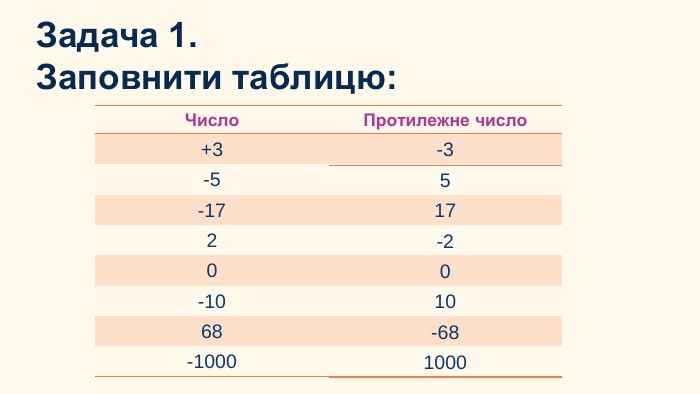
Презентація "Модуль числа" (Тарасенкова Н.А., № 21)
Про матеріал
Сучасна презетація на темою "Модуль числа" за підручником з математики Тарасенкової Н.А.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку