Презентація на тему "Куб. 5 клас"
Про матеріал
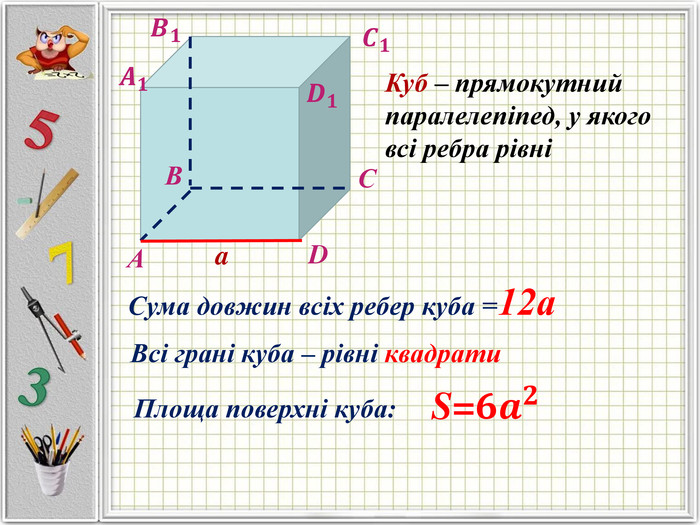
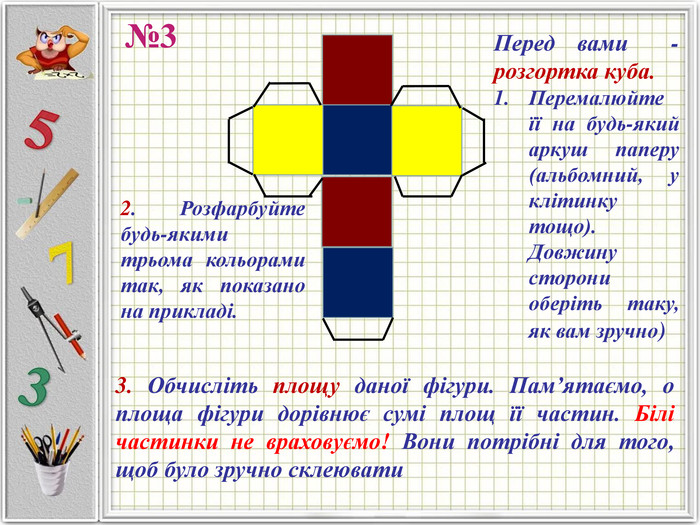
Презентація призначена для вивчення теми "Куб" в 5 класі, після вивчення теми "Прямокутний паралелепіпед". На початку уроку повторюються основні відомості про прямокутний паралелепіпед, розглядаються особливості куба, наводяться приклади стандартних задач, розв'язується компетеннісна задача з підручника. Наприкінці презентації пропонується творче домашнє завдання. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку