Презентація "Об’єм призми"

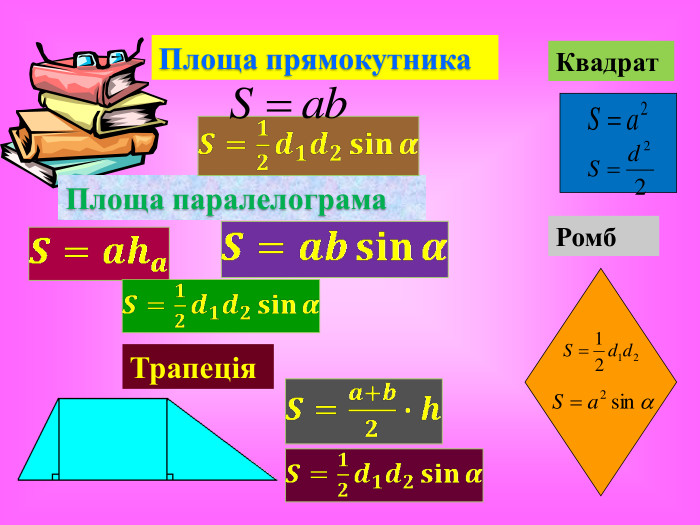
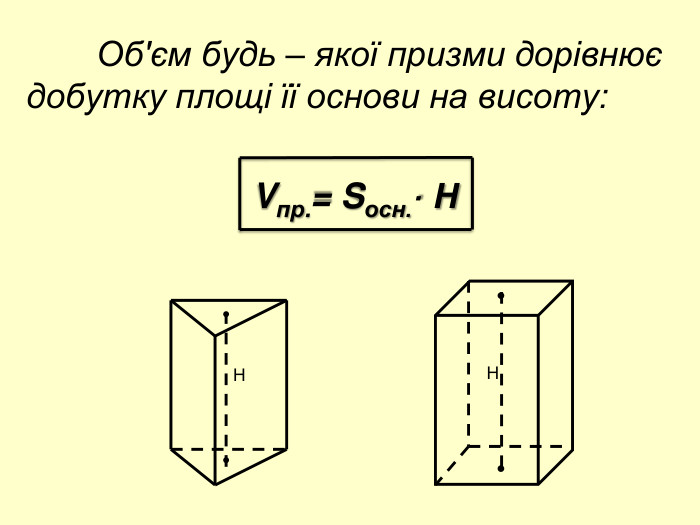
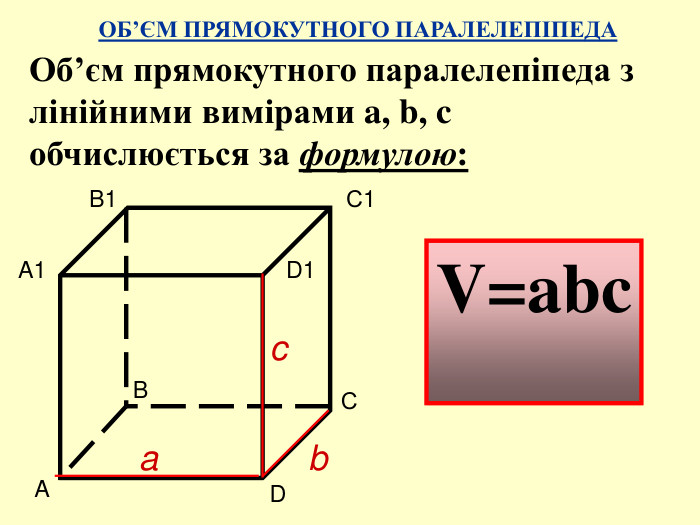
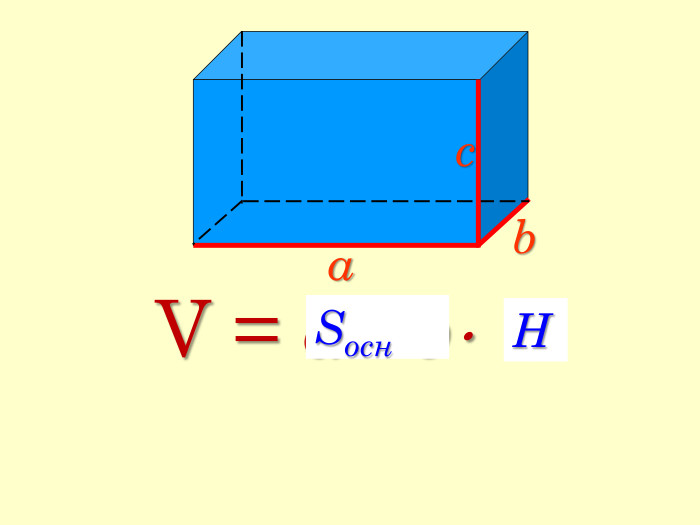
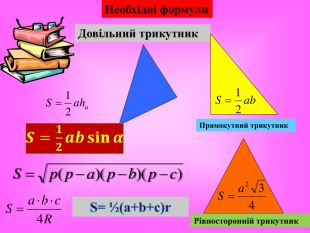
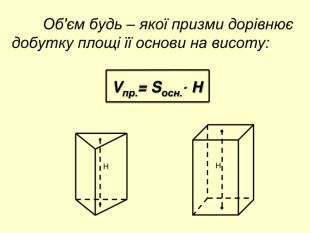
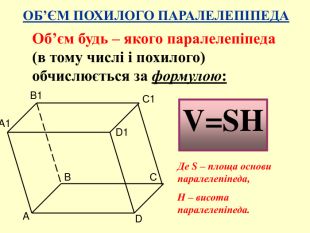
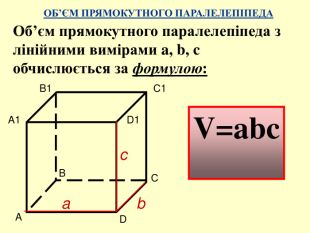
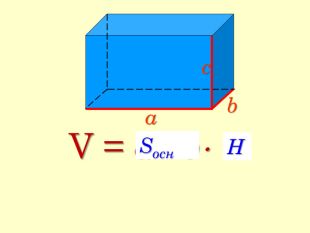
Мета: Вивчити зміст поняття «об’єм тіла», формули для обчислення об’ємів призми, куба та паралелепіпеда. Формувати основні методи обчислення об’ємів, вміння узагальнювати, робити висновки, проводити міркування. Розвивати просторове мислення учнів, вміння використовувати геометричні конструкції у прикладних задачах з метою вимірювання об’ємів, здатність висловлювати свою думку, інтерес до предмета. Виховувати відповідальне ставлення до навчання. Показати важливість геометричних знань, умінь та навичок людям багатьох професій.

Цели урока: Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике.

ПОНЯТТЯ ОБ’ЄМУ Для геометричних тіл об’єм – це додатна величина, числове значення якої має такі властивості: 1. Рівні тіла мають рівні об’єми. 2. Якщо тіло розбито на частини, які є простими тілами, то об’єм цього тіла дорівнює сумі об’ємів його частин. 3. Об’єм куба, ребро якого дорівнює одиниці довжини, дорівнює одній кубічній одиниці. Об'єм – це частина простору, яку займає тіло.

З історії розвитку поняття об’єму геометричних тіл. Евклід Приблизно 330 – 277 до н.е. У творах Архімеда та “Началах” Евкліда були виведені формули для знаходження об'ємів многогранників і деяких тіл обертання (циліндра, кулі, конуса та їх частин). Розробив теорію площ і об'ємів К.М.Е.Жордан (1838 - 1922) – французький математик, один із засновників сучасної математики. У минулому одиницями вимірювання об'ємів біли міри посудини, що використовувалися для зберігання сипучих і рідких речовин. У давнину деякі міри маси і об'єму часто збігалися з мірами вартості товару – грошовими одиницями. Зокрема, на Русі основна одиниця маси – гривня – була водночас грошовою одиницею. Гривня – це злиток срібла, маса якого наближено дорівнювала 1 фунту. У другій половині ХІІІ ст. гривну почали рубати навпіл і називати рублем, який із Х\/ став основною грошовою одиницею.

Прямокутний трикутник Рівносторонній трикутник Довільний трикутник Необхідні формули

Площа прямокутника Площа паралелограма Ромб Квадрат Трапеція

Об'єм будь – якої призми дорівнює добутку площі її основи на висоту: Vпр.= Sосн.· Н ● ● Н ● ● Н

ОБ’ЄМ ПОХИЛОГО ПАРАЛЕЛЕПІПЕДА Об’єм будь – якого паралелепіпеда (в тому числі і похилого) обчислюється за формулою: V=SH A B С D A1 B1 D1 С1 Де S – площа основи паралелепіпеда, H – висота паралелепіпеда.

a b c A B С D A1 B1 D1 С1 ОБ’ЄМ ПРЯМОКУТНОГО ПАРАЛЕЛЕПІПЕДА Об’єм прямокутного паралелепіпеда з лінійними вимірами a, b, c обчислюється за формулою: V=abc

a b V = a b c Sосн H c

Об ’ єм куба. a 3 см

Використай свої знання 1. Відро вміщує приблизно 12 літрів. Скільки необхідно відер води, щоб заповнити скляний куб, ребро якого 1м? 2. Класні приміщення повинні бути розраховані так, щоб на одного учня було не менше 6 мі повітря. Чи можуть у класному приміщенні, яке має вигляд прямокутного паралелепіпеда з вимірами 8,5 м, 6 м, і 3,5 м, навчатися 30 учнів без порушень санітарних норм? 3. .Три куба, зроблені з свинца, мають ребра 3, 4 и 5 см. Вони переплавлені в один куб. Знайти його ребро. 4. Ванна має форму прямокутного паралелепіпеда з вимірами 60см, 1м 60см і 70см. Чи поміститься у ванні 1мі води? 5. 1мі золота важить приблизно 19т. Чи може людина підняти куб золота, ребро якого 20см?

Задача №6 У кондитерський цех надійшли ящики для цукерок Гулівер. Чи помістяться в ящик розміром 38 Ч 29 Ч 11 см. а) 200 шт, б) 300 шт. Розміри однієї цукерки 8 Ч 3,5 Ч 2 см.

ДЯКУЄМО ЗА УРОК!