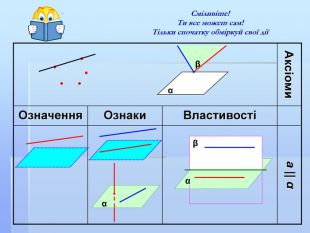
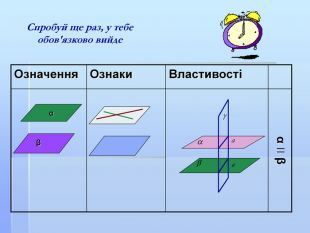
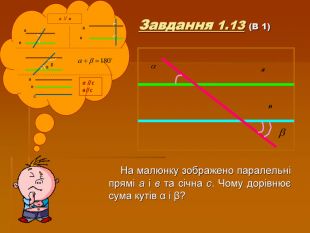
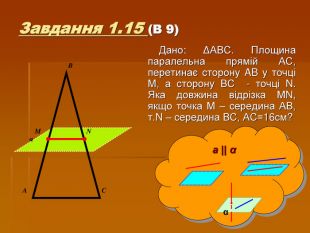
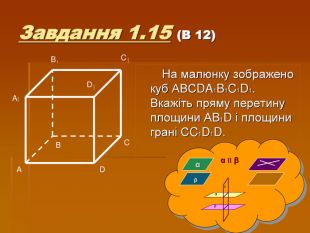
Презентація " Паралельність у просторі"
Про матеріал
Матеріал до підсумкового уроку за темою: "Узагальнююче повторення з теми: Паралельність прямих і площину у просторі". У презентації взаємозв'язок з професією "електрогазозварник , автослюсар"
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Щиро дякую!
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







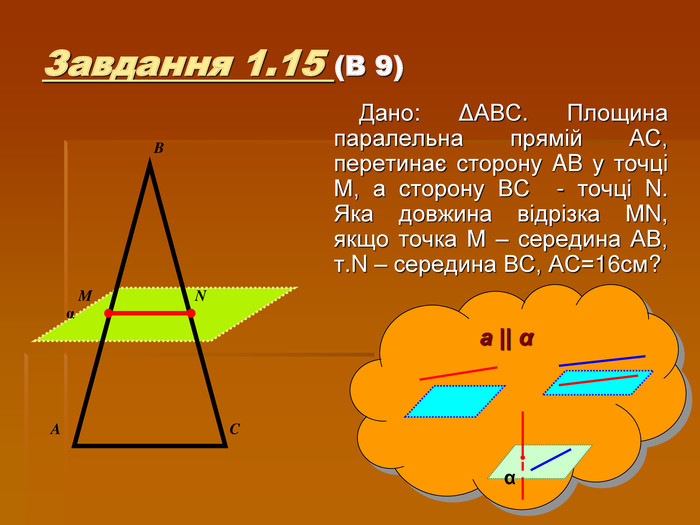











![Завдання групи № 1 Визначити розрахункові підсилення у стиковому з’єднанні, виконаному за допомогою ручного зварювання з урахуванням звичайних способів контролю, якщо δ = 0,01м, ℓ = 0,2м та Вказівка: - розрахунковий опір металу стикових швів встановлюється СНіП (Н/м2). Стикові шви на міцність розраховуються за формулою , де N – розрахункова повздовжня сила, яка діє на з’єднання, [ H ]. δ- товщина металу у розрахунковому перерізі, [м], ℓ- довжина шва, [м]. Завдання групи № 1 Визначити розрахункові підсилення у стиковому з’єднанні, виконаному за допомогою ручного зварювання з урахуванням звичайних способів контролю, якщо δ = 0,01м, ℓ = 0,2м та Вказівка: - розрахунковий опір металу стикових швів встановлюється СНіП (Н/м2). Стикові шви на міцність розраховуються за формулою , де N – розрахункова повздовжня сила, яка діє на з’єднання, [ H ]. δ- товщина металу у розрахунковому перерізі, [м], ℓ- довжина шва, [м].](/uploads/files/225720/70754/75349_images/25.jpg)
![Вказівка: Максимальне підсилення N для кутових лобових швів розраховується за формулою: де k – катет шва, [м], ℓ- довжина шва, [м], - розрахунковий опір зрізу, [Н/м2]. Коефіцієнт 0,7 показує, що розрахунок ведеться з можливого руйнування шва по гіпотенузі прямокутного трикутника (форма перерізу кутового шва). Завдання групи № 2 Визначити розрахункове підсилення у напускному з’єднанні з лобовим швом, якщо k = 0,001м, ℓ = 0,2м. Вказівка: Максимальне підсилення N для кутових лобових швів розраховується за формулою: де k – катет шва, [м], ℓ- довжина шва, [м], - розрахунковий опір зрізу, [Н/м2]. Коефіцієнт 0,7 показує, що розрахунок ведеться з можливого руйнування шва по гіпотенузі прямокутного трикутника (форма перерізу кутового шва). Завдання групи № 2 Визначити розрахункове підсилення у напускному з’єднанні з лобовим швом, якщо k = 0,001м, ℓ = 0,2м.](/uploads/files/225720/70754/75349_images/26.jpg)
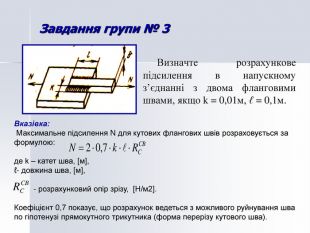
![Завдання групи № 3 Визначте розрахункове підсилення в напускному з’єднанні з двома фланговими швами, якщо k = 0,01м, ℓ = 0,1м. Вказівка: Максимальне підсилення N для кутових флангових швів розраховується за формулою: де k – катет шва, [м], ℓ- довжина шва, [м], - розрахунковий опір зрізу, [Н/м2]. Коефіцієнт 0,7 показує, що розрахунок ведеться з можливого руйнування шва по гіпотенузі прямокутного трикутника (форма перерізу кутового шва). Завдання групи № 3 Визначте розрахункове підсилення в напускному з’єднанні з двома фланговими швами, якщо k = 0,01м, ℓ = 0,1м. Вказівка: Максимальне підсилення N для кутових флангових швів розраховується за формулою: де k – катет шва, [м], ℓ- довжина шва, [м], - розрахунковий опір зрізу, [Н/м2]. Коефіцієнт 0,7 показує, що розрахунок ведеться з можливого руйнування шва по гіпотенузі прямокутного трикутника (форма перерізу кутового шва).](/uploads/files/225720/70754/75349_images/27.jpg)