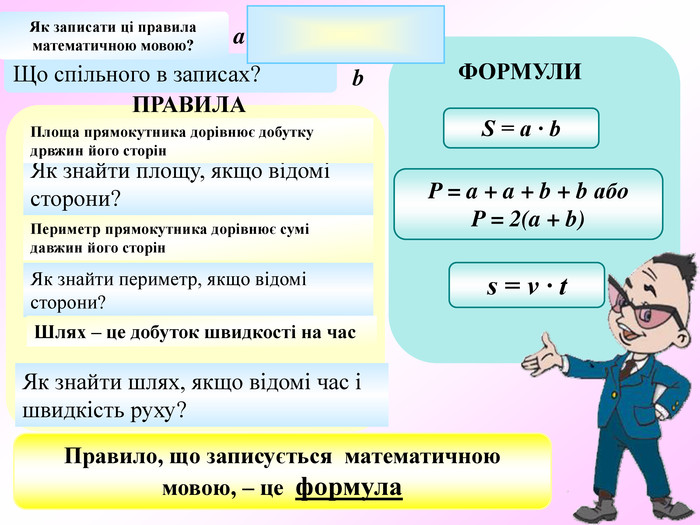
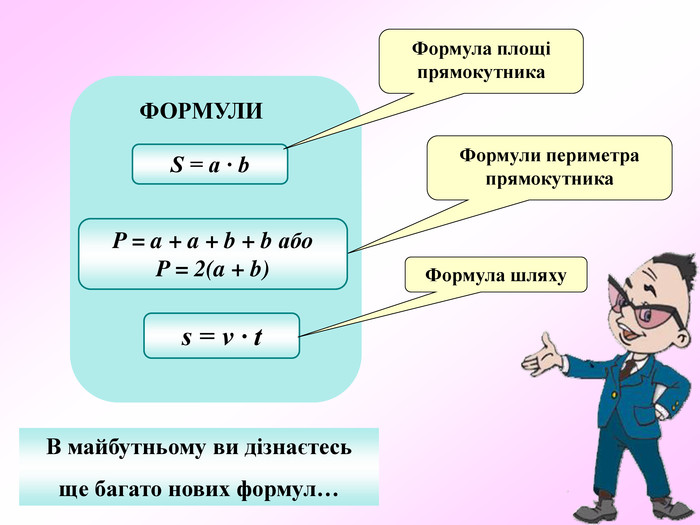
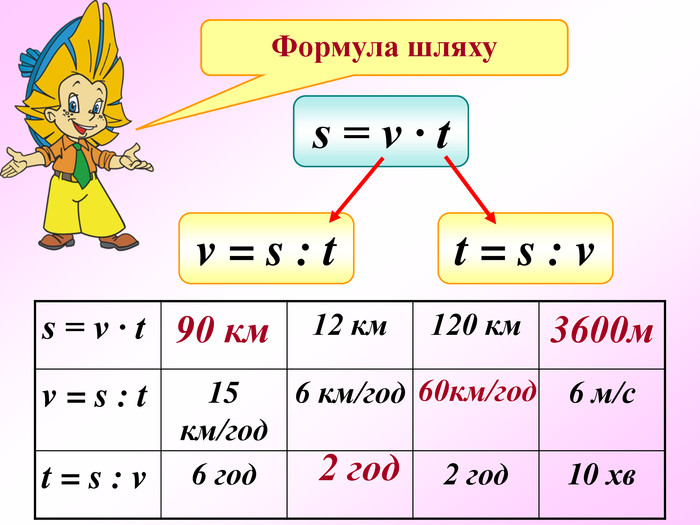
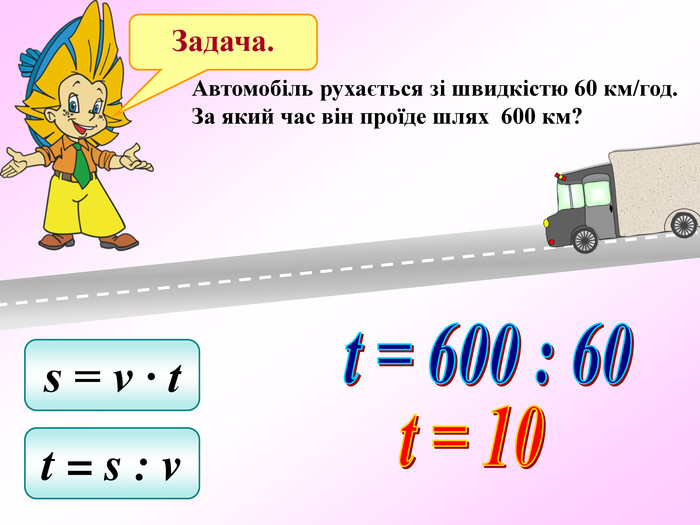
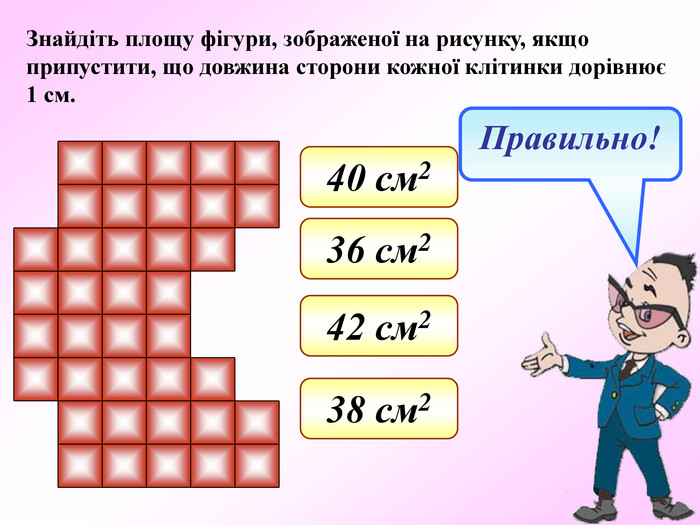
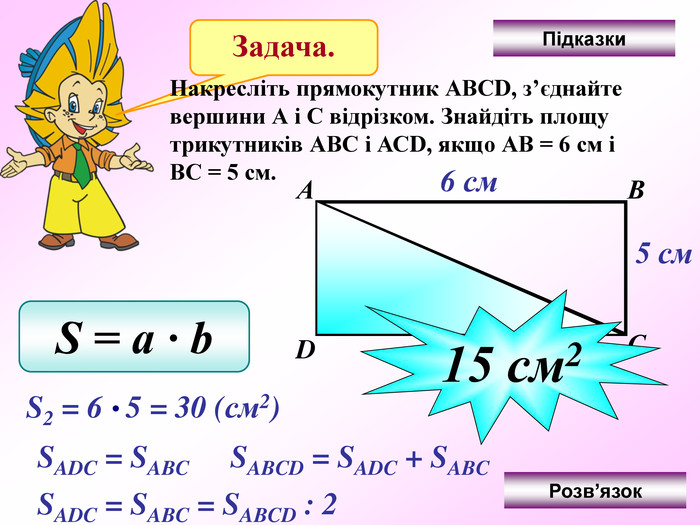
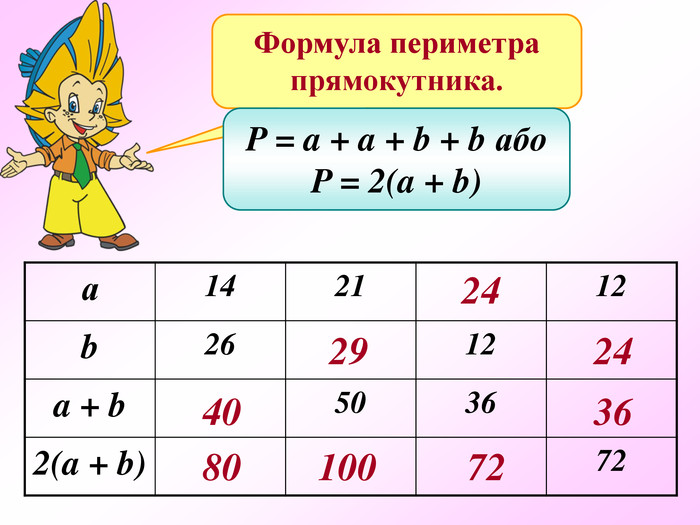
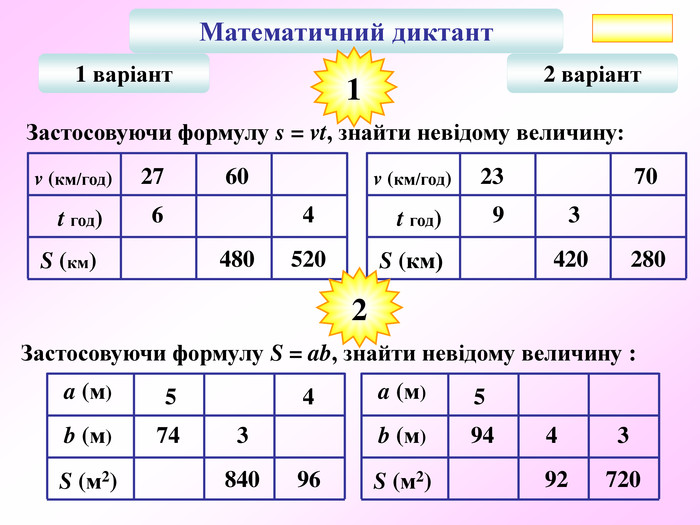
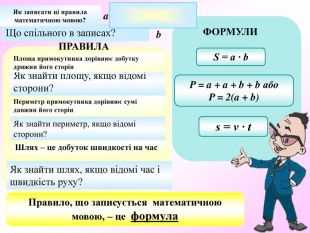
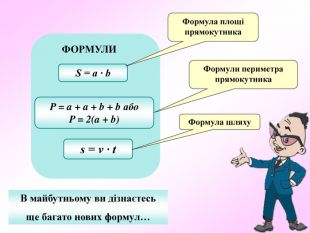
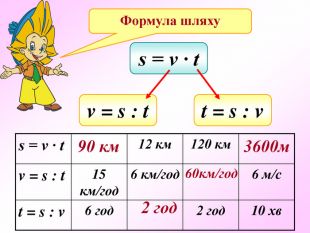
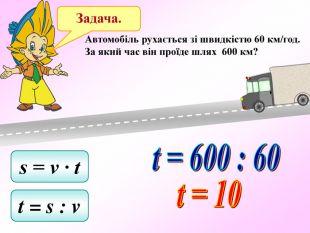
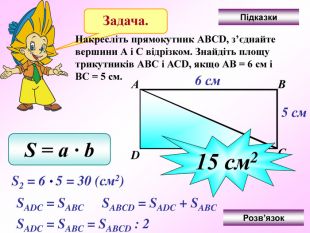
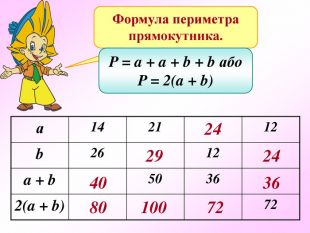
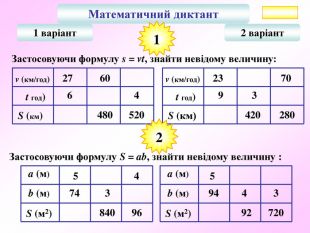
Презентація по темі "Формули"
Про матеріал
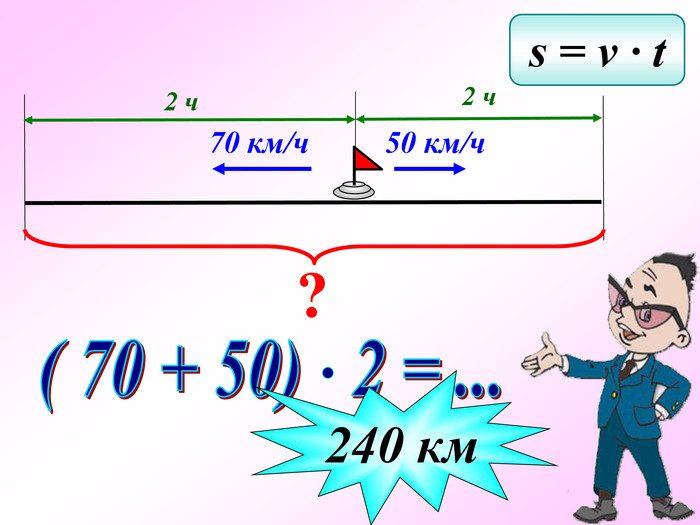
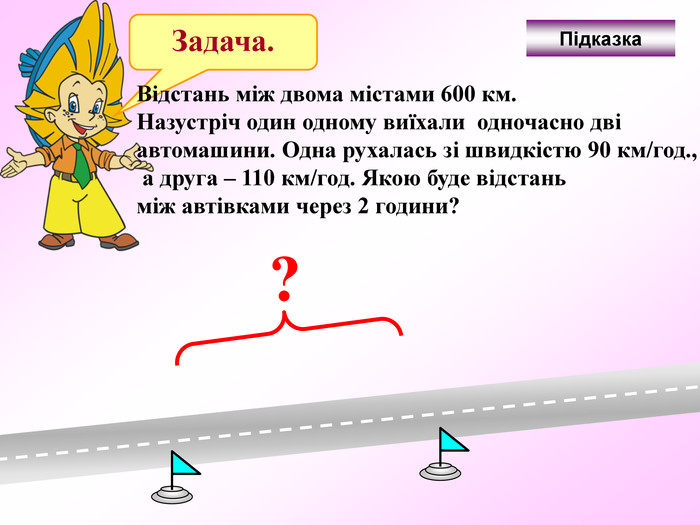
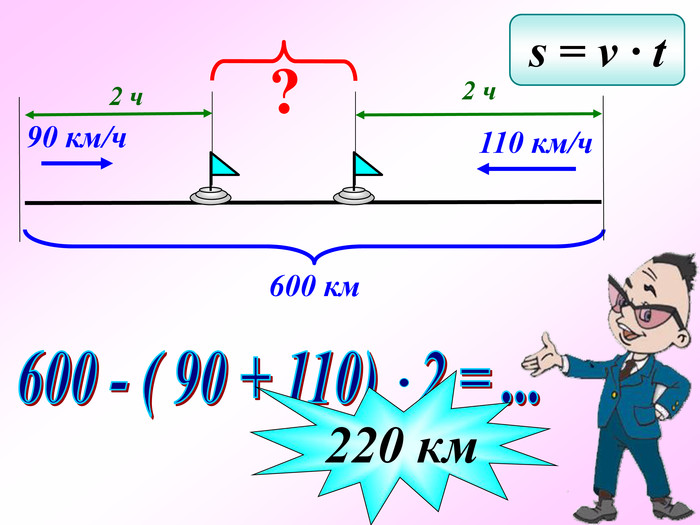
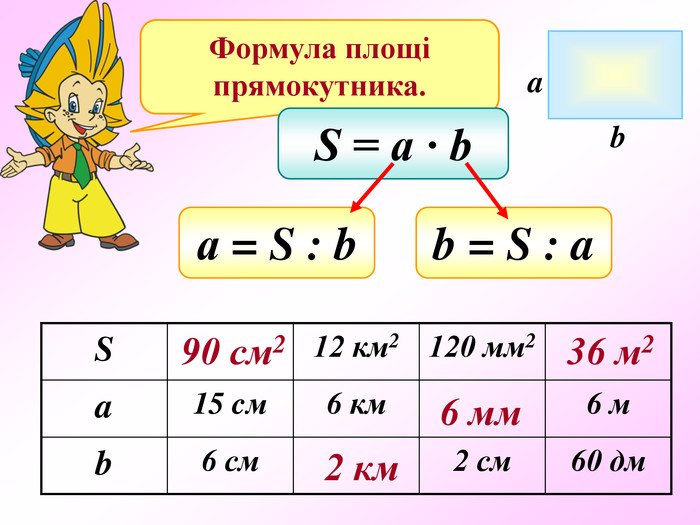
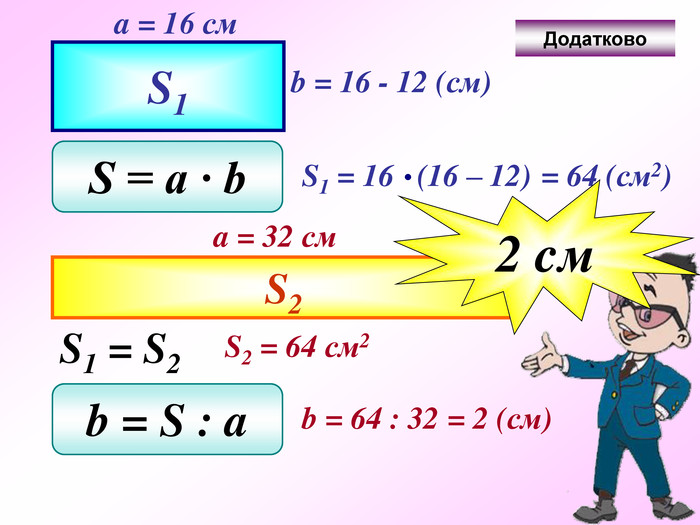
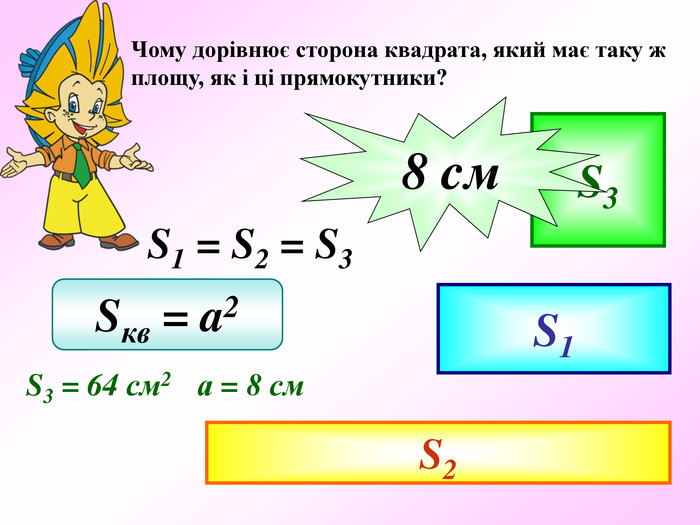
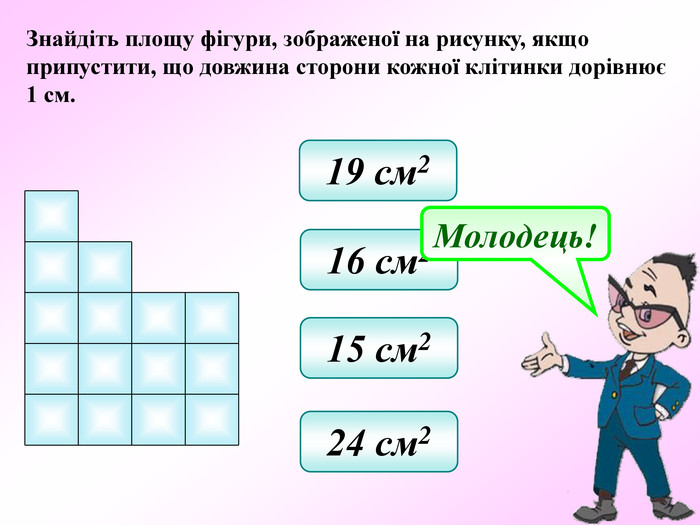
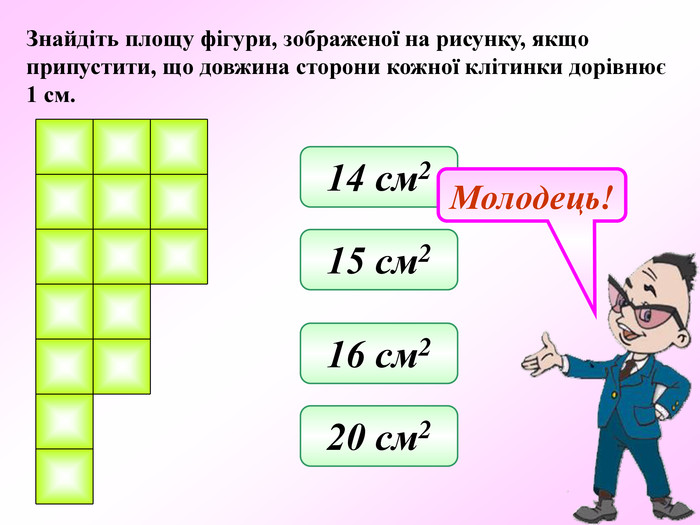
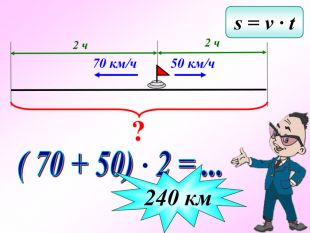
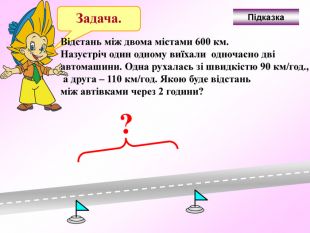
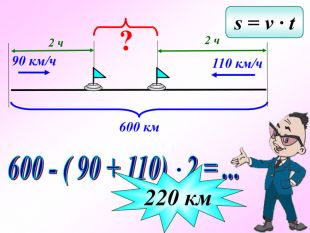
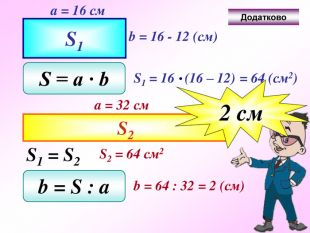
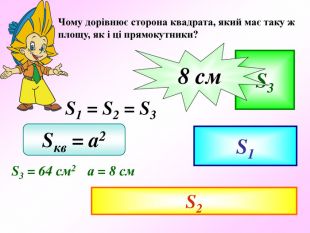
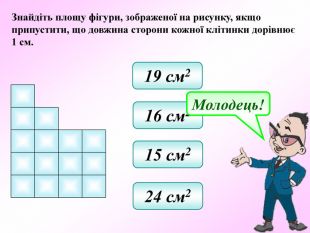
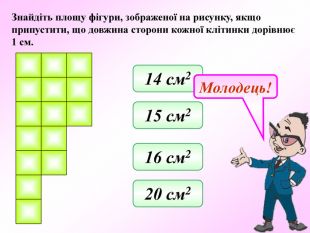
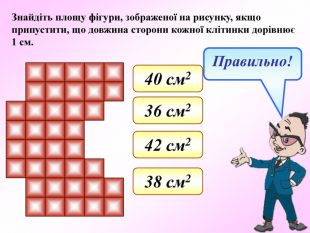
Презентація - це допомога вчителю у проведенні уроку. Більшість учнів мають зорову пам'ять і їм значно простіше засвоїти новий матеріал, коли вони бачать перед собою ці формули у презентації, а не написані на класній дошці крейдою.
Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку