Презентація "Системи лінійних рівнянь із двома змінними. Методи розв'язування"

Системи лінійних рівнянь із двома змінними. Методи розв'язування вчитель математики Осинівської гімназіїТретяк Тамара Миколаївна

Мета:формувати поняття лінійного рівнянння з двома змінними, системи лінійних рівнянь з двома змінними та вміння їх розв’язувати різними способами;розвивати увагу, уміння порівнювати, аналізувати, робити висновки;виховувати відповідальність, самостійність, любов до навчання та вміння працювати разом.

Обладнання: Онлайн-калькулятор https://www.desmos.com/calculator?lang=ru

План. Лінійне рівняння з двома змінними. Системи рівнянь з двома змінними. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними. Розв'язування системи лінійних рівнянь методом підстановки Розв'язування системи лінійних рівнянь методом додавання

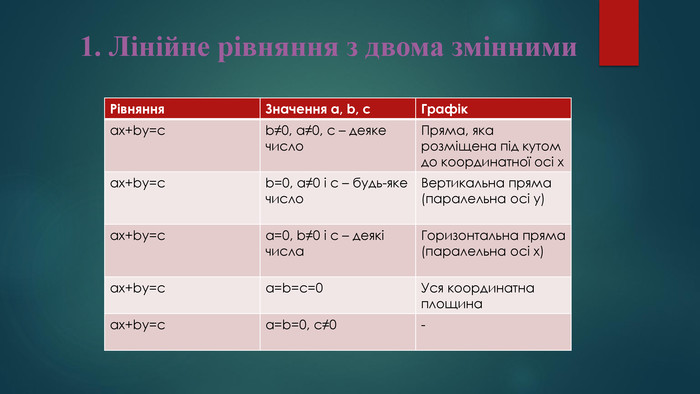
1. Лінійне рівняння з двома змінними Означення. Лінійним рівнянням із двома змінними називають рівняння виду ах+by=c, де х і y – змінні, a,b,c – деякі числа. Приклади лінійних рівнянь:3х+2y= 450 Х+ y=900х+5y=-1-3х+0y=50х+0y=00х+0y=2 Назвіть значення a, b, c у поданих лінійних рівняннях.

1. Лінійне рівняння з двома змінними Означення. Розв'язком лінійного рівняння з двома змінними називають пару чисел (x,y), яка перетворює дану рівність в правильну. Наприклад:x+y = 90(20, 70)(5, 85)(0,90)

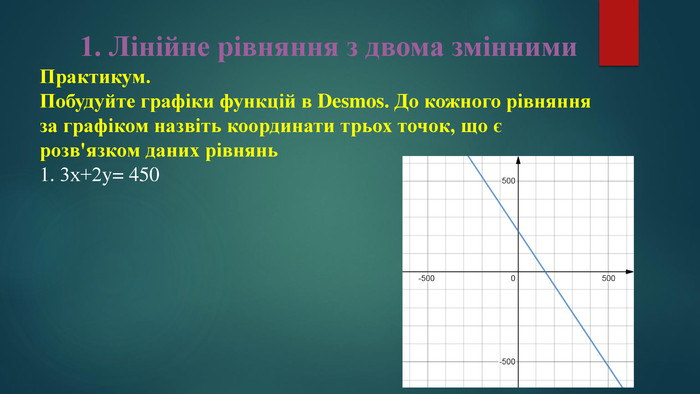
1. Лінійне рівняння з двома змінними Означення. Графіком лінійного рівняння з двома змінними є пряма, яка містить точки площини, координати яких є розв'язком даного рівняння Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівняньhttps://www.desmos.com/calculator?lang=ru1. 3х+2y= 4502. Х+ y=903. 0х+5y=-14. -3х+0y=55. 0х+0y=06. 0х+0y=2

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь1. 3х+2y= 450

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь2. x+ y=90

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь3. 0х+5y=-1

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь4. -3х+0y=5

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь5. 0х+0y=0

1. Лінійне рівняння з двома змінними Практикум. Побудуйте графіки функцій в Desmos. До кожного рівняння за графіком назвіть координати трьох точок, що є розв'язком даних рівнянь6. 0х+0y=2

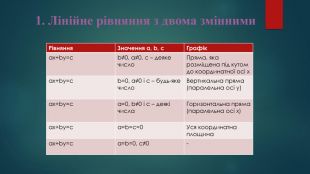
1. Лінійне рівняння з двома змінними {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Рівняння. Значення a, b, c. Графікax+by=cb≠0, a≠0, c – деяке число. Пряма, яка розміщена під кутом до координатної осі хax+by=cb=0, a≠0 і c – будь-яке число. Вертикальна пряма (паралельна осі y)ax+by=ca=0, b≠0 і c – деякі числа. Горизонтальна пряма(паралельна осі х)ax+by=ca=b=с=0 Уся координатна площинаax+by=ca=b=0, c≠0-

2. Системи рівнянь з двома змінними Якщо необхідно знайти спільний розв'язок кількох рівнянь, то говорять, що треба розв'язати систему рівнянь. Задача. Знайдіть сторони прямокутника, площа якого дорівнює 12 см², а периметр – 14 см.{xy=122x+2y=14

2. Системи рівнянь з двома змінними Якщо необхідно знайти спільний розв'язок кількох рівнянь, то говорять, що треба розв'язати систему рівнянь{Задача. Знайдіть координати спільних точок двох прямих -6x+5y=9 і 4x+3y=13-6x+5y=9 4x+3y=13

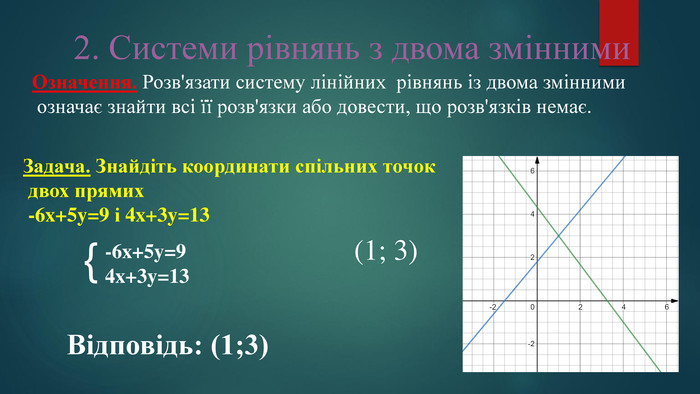
2. Системи рівнянь з двома змінними {Задача. Знайдіть координати спільних точок двох прямих -6x+5y=9 і 4x+3y=13-6x+5y=9 4x+3y=13 Означення. Розв'язком системи лінійних рівняннь із двома змінними називають пару значень змінних (x,y), яка перетворює кожне рівняння в правильну рівність(1; 3)

2. Системи рівнянь з двома змінними {Задача. Знайдіть координати спільних точок двох прямих -6x+5y=9 і 4x+3y=13-6x+5y=9 4x+3y=13 Означення. Розв'язати систему лінійних рівнянь із двома змінними означає знайти всі її розв'язки або довести, що розв'язків немає. (1; 3)Відповідь: (1;3)

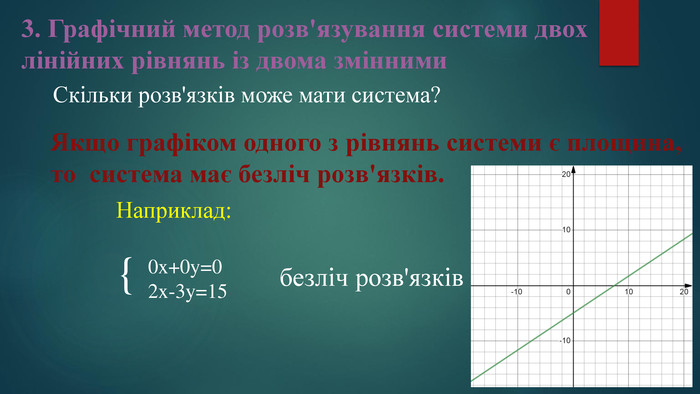
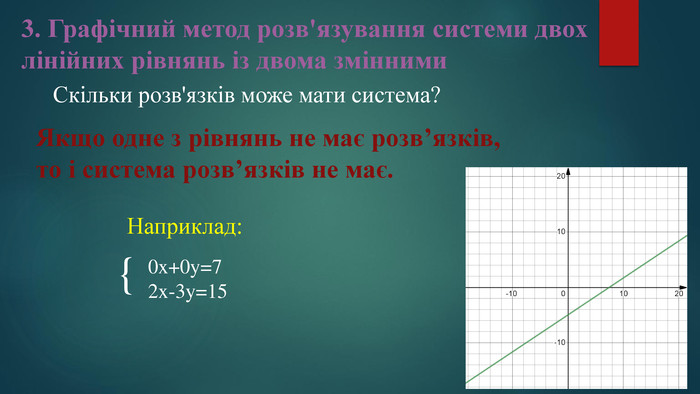
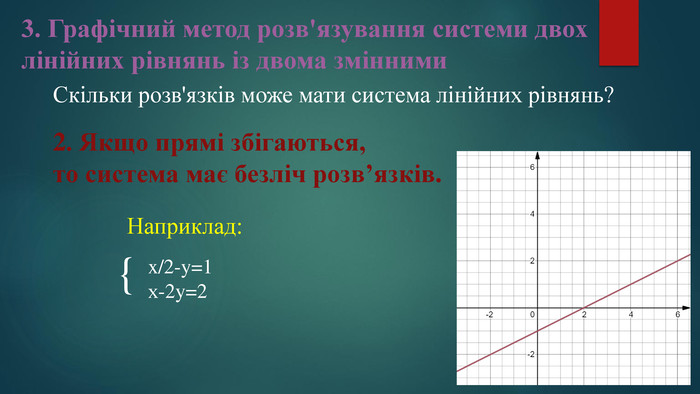
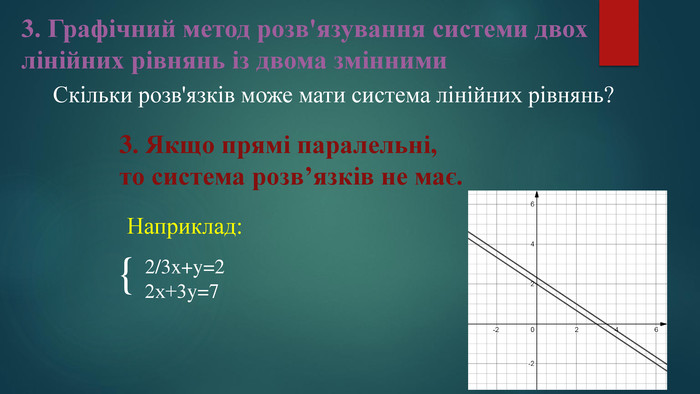
3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Алгоритм (графічний метод)Побудувати на одній координатній площині графіки рівнянь, що входять до системи.2. Знайти координати точок перетину побудованих графіків.3. Визначені пари точок вказати у відповіді

3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Скільки розв'язків може мати система?Якщо графіком одного з рівнянь системи є площина, то система має безліч розв'язків. Наприклад: {0x+0y=02x-3y=15безліч розв'язків

3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Скільки розв'язків може мати система?Якщо одне з рівнянь не має розв’язків, то і система розв’язків не має. Наприклад: {0x+0y=72x-3y=15

3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Скільки розв'язків може мати система лінійних рівнянь?1. Якщо прямі перетинаються, то система має один розв’язок. Наприклад: {-6x+5y=94x+3y=13

3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Скільки розв'язків може мати система лінійних рівнянь?2. Якщо прямі збігаються, то система має безліч розв’язків. Наприклад: {x/2-y=1х-2y=2

3. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними Скільки розв'язків може мати система лінійних рівнянь?3. Якщо прямі паралельні, то система розв’язків не має. Наприклад: {2/3x+y=22х+3y=7

4. Розв'язування системи лінійних рівнянь методом підстановки 1. Виразимо з будь-якого рівняння одну змінну через другу{2х+y=114x-y=71 крок: у=11- 2х

4. Розв'язування системи лінійних рівнянь методом підстановки 2. Підставимо в інше рівняння системи замість змінної вираз, отриманий на першому кроці4x-y=72х+y=11{1 крок: у=11- 2х2 крок: 4х –(11-2х)=7

4. Розв'язування системи лінійних рівнянь методом підстановки 4x-y=72х+y=11{1 крок: у=11- 2х2 крок: 4х –(11-2х)=73. Розв'язати одержане рівняння 3 крок: 4х –(11-2х)=7 4х –11+2х=7 6х=7+11 6х=18 х=3

4. Розв'язування системи лінійних рівнянь методом підстановки 4x-y=72х+y=11{1 крок: у=11- 2х2 крок: 4х –(11-2х)=74. Підставити одержане значення змінної у вираз, отриманий на першому кроці та обчислити значення другої змінної3 крок: 4х –11+2х=7 6х=7+11 6х=18 х=34 крок: у=11- 2х у= 11- 2*3 у= 5

4. Розв'язування системи лінійних рівнянь методом підстановки 4x-y=72х+y=11{1 крок: у=11- 2х2 крок: 4х –(11-2х)=74. Підставити одержане значення змінної у вираз, отриманий на першому кроці та обчислити значення другої змінної3 крок: 4х –11+2х=7 6х=7+11 6х=18 х=34 крок: у= 11- 2*3 у= 55 крок: Відповідь: (3,5)

4. Розв'язування системи лінійних рівнянь методом підстановки Алгоритм 1. Виразити з будь-якого рівняння одну змінну через другу2. Підставити в інше рівняння системи замість змінної вираз, отриманий на першому кроці3. Розв'язати одержане рівняння 4. Підставити одержане значення змінної у вираз, отриманий на першому кроці та обчислити значення другої змінної5. Дати відповідь

5. Розв'язування системи лінійних рівнянь методом додавання. Помножити одне чи обидва рівняння системи на множники такі, щоб при одній із змінних одержати протилежні коефіцієнти7х+2у=117х+6у=-9{7х+2у=1| * (-3)17х+6у=-9 1 крок-{-21х-6у=-317х+6у=-9 {

5. Розв'язування системи лінійних рівнянь методом додавання2. Почленно додати ліві і праві частини рівнянь, одержаних на першому кроці{7х+2у=1| * (-3)17х+6у=-9 1 крок-{-21х-6у=-317х+6у=-9 2 крок --4х=-12

5. Розв'язування системи лінійних рівнянь методом додавання3. Розв'язати рівняння з однією змінною, яке ми отримали на другому кроці.{7х+2у=1| * (-3)17х+6у=-9 1 крок-{-21х-6у=-317х+6у=-9 2 крок --4х=-123 крок - Х=3

5. Розв'язування системи лінійних рівнянь методом додавання4. Підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи і обчислити значення другої змінної.{7х+2у=1| * (-3)17х+6у=-9 1 крок-{-21х-6у=-317х+6у=-9 2 крок --4х=-123 крок - Х=34 крок - 7х+2у=17*3+2у=12у=1-212у=20у=10

5. Розв'язування системи лінійних рівнянь методом додавання5. Записати відповідь{7х+2у=1| * (-3)17х+6у=-9 1 крок-{-21х-6у=-317х+6у=-9 2 крок --4х=-123 крок - Х=34 крок - 7х+2у=17*3+2у=12у=1-212у=20у=105 крок - Відповідь: (3;10)

5. Розв'язування системи лінійних рівнянь методом додавання. Алгоритм. Помножити одне чи обидва рівняння системи на множники такі, щоб при одній із змінних одержати протилежні коефіцієнти2. Почленно додати ліві і праві частини рівнянь, одержаних на першому кроці3. Розв'язати рівняння з однією змінною, яке ми отримали на другому кроці.4. Підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи і обчислити значення другої змінної.5. Записати відповідь

Практикум. Розв'язати систему лінійних рівнянь усіма способами:{х-у=1х+2у=7 Відповідь: (3;2)

Практикум. Розв'язати систему лінійних рівнянь усіма способами:{х-3у=54х+9у=41 Відповідь: (8;1)

На уроці я: Дізнався(лася) …Зрозумів(ла)…Навчився(ся)…Мій успіх в тому, що я …Я відчув(ла) труднощі, коли…Було важко, але я…Наступного разу я…Мій настрій після уроку…

Література. А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. Алгебра 7 клас. Підручник.2. Янченко Г., Янченко В., Янченко О. Алгебра 7 клас: Книга для вчителя .3. Возняк Г., Возняк О. Тестові завдання з алгебри. 7 клас