Презентація. Системи лінійних рівнянь як математичні моделі текстових задач
Про матеріал
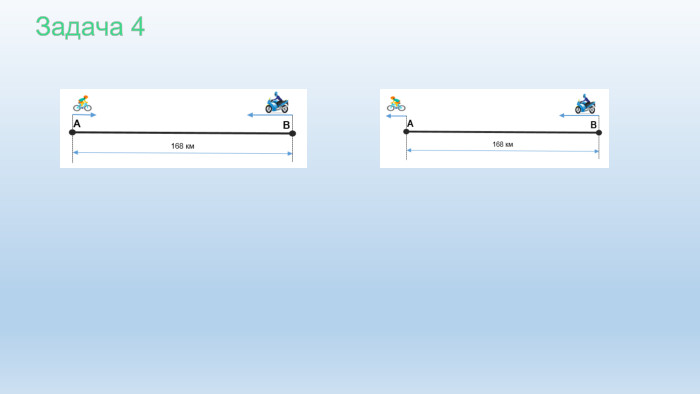
Презентація "Системи лінійних рівнянь як математичні моделі текстових задач". Алгебра 7 клас.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую!


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку