Формули скороченого множення

“Формули скороченого множення”

Тема уроку: “Підсумковий урок по темі: формули скороченого множення”

Мета уроку: “Узагальнити знання учнів по темі, в ігровій формі поглибити знання учнів по трьох способах розкладу многочлена на множники, ознайомити учнів з історичними витоками утворення формул скороченого множення”.

      “Розвивати в учнів логічне мислення, навички застосування формул при обчисленні та спрощенні виразів, розв’язуванні рівнянь”

      “Виховувати в учнів інтерес до пізнавальної діяльності, ціленаправленість, організованість, згуртованість, вміння колективу класу діяти в різних навчальних ситуаціях.”

Метод: Репродуктивність.

Обладнання: Дидактичний матеріал, карточки, кодоскоп.

Хід уроку

І. Геометрична інтерпретація формул , .

Історичні відомості (доповідь учня).

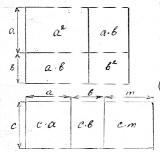Формули скороченого множення стародавнім китайським і грецьким математиком були відомі за багато віків до початку нашої ери. Записували їх тоді не за допомогою букв, а словами, і доводили геометрично (тільки для додатніх чисел). Користуючись малюнком, пояснювали, що для будь – яких чисел площа квадрата із стороною дорівнює сумі площ двох квадратів із сторонами і двох прямокутників із сторонами . Отже .

Завдання учням: . Обґрунтуйте цю рівність за допомогою малюнка. Який це закон у математиці?

Учитель ставить перед учнями мету: обґрунтувати в кінці уроку яку роль відіграють формули скороченого множення при перетворенні математичних виразів?

ІІ. Слуховий диктант “Добрий настрій” (з хлопками на неправильну відповідь).

III. Усно або майже усно.(По мірі необхідності допомагає вчитель)

IV. Гра “Дивись, не помились!” (Заповнити пусті кліточки ). (Клас розбивається на три команди. Завдання виконуються на швидкість.)

  І-В       ІІ-В

      III-В

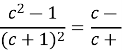
Кожній команді за правильну відповідь нараховується по 1 очку та за швидкість виконання відповідно по 2 очка, 1 очку та 0 очок (Відповіді перевіряються з допомогою кодоскопа).

V. Гра “Постріл в мішень.” Самостійна робота на два варіанти. Завдання: розкласти на множники. Кожен учень отримує карточку. На виконання завдання дається 10-15 хв.

          І-В           ІІ-В

Додаткові:    

За кожне правильно зроблене завдання ставиться 2 бали, за додаткове ставляться бали окремо.

VI. Конкурс “Найкращий знавець.” Вибірковий тур:

1. Що означає розв’язати рівняння?
2. Що таке корінь рівняння?
3. Як знайти у рівнянні невідомий множник?
4. Які додатки називаються подібними?
5. Які способи розкладу на множники многочлена ви знаєте?
6. Що означає у математиці коефіцієнт?

Відбирається 3-5 учнів, які при виконанні завдань біля дошки мають право на дві підказки: “допомога класу” та “допомога друга.”

Завдання.

1.       Довести, що при будь –якому  натуральному числу вираз .
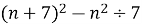2.       Розв’яжіть рівняння. .
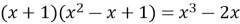3.       Довести, що три останні цифри числа – нулі.
4.       Розв’яжіть рівняння. .
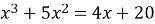5.       Доведи, що квадрат будь – якого непарного числа, зменшений на 1, ділиться на 4.
6.       Софізм “4=5.”

Учень біля дошки пояснює, що софізм, це доведене твердження, але при  доведенні використовується математична помилка, яку учням необхідно знайти.

“Доведемо, що .  , , ,  ,  ,  ,  .”  – де помилка?

7.       Підсумок уроку.

•  Яку роль відіграють формули скороченого множення при перетворенні математичних виразів?

8.                   Домашнє завдання