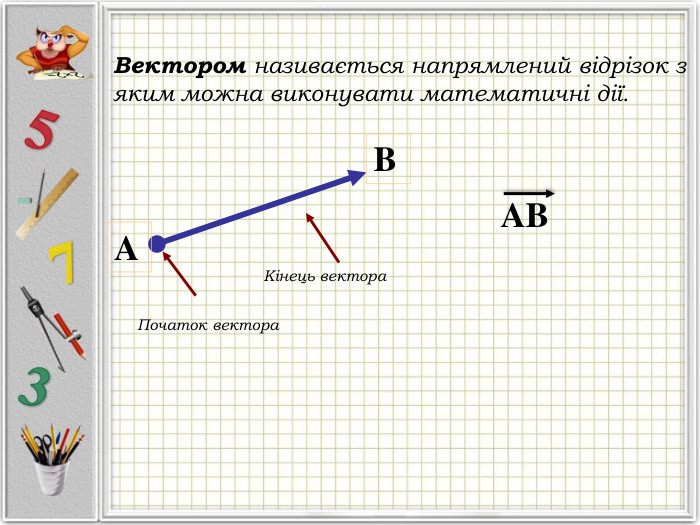
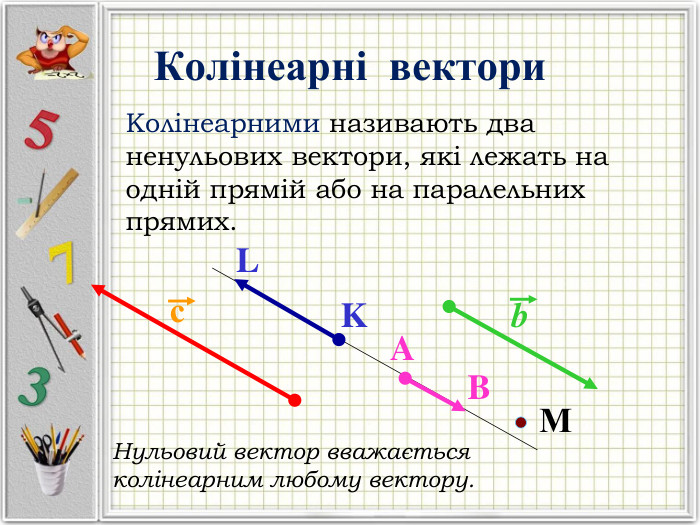
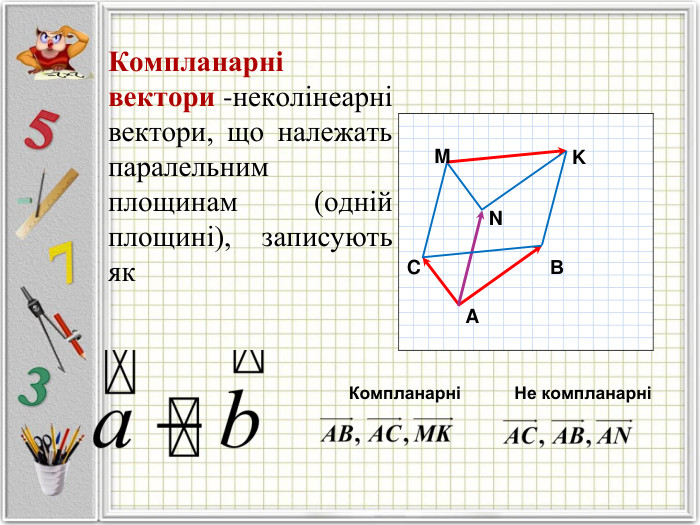
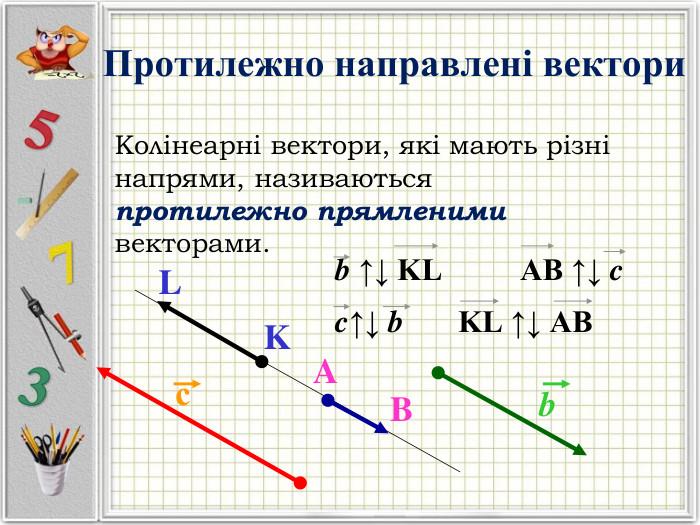
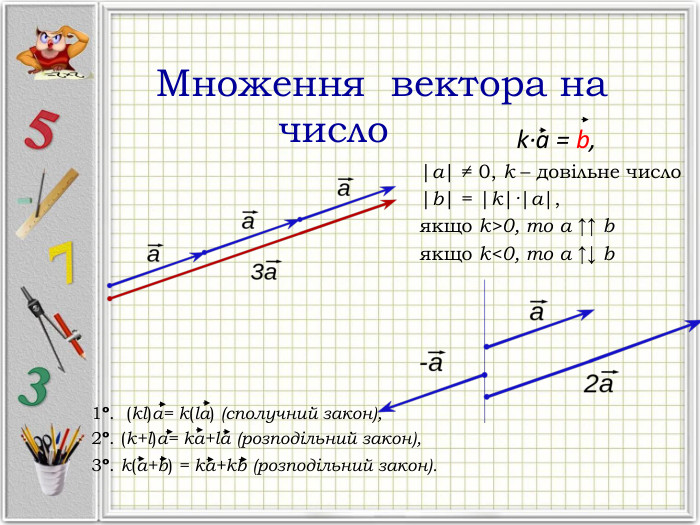
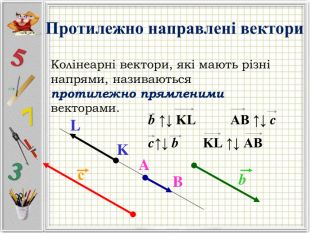
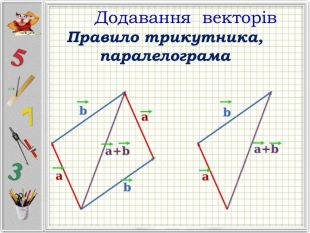
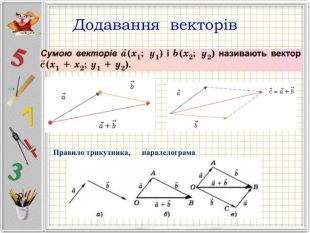
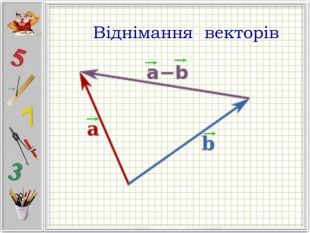
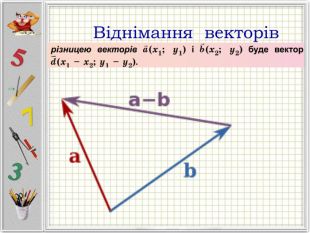
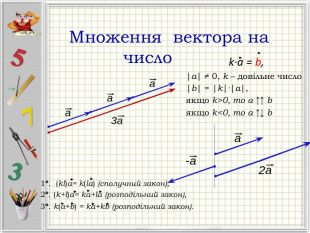
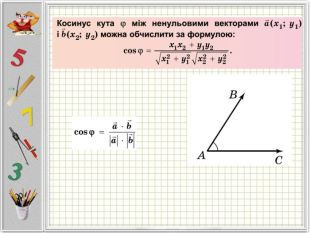
Презентація "Вектори. Підготовка до НМТ".
Про матеріал
Мета презентації: узагальнення та систематизація знань та вмінь з теми; допомогти в підготовці до НМТ. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку