Презентація "Використання формул скороченого множення для розкладання многочленів на множники"
Про матеріал
Презентація до уроку узагальнення знань з теми "Розкладання на множники многочленів за допомогою формул скороченого множення".
У презентації викладений як теоретичний матеріал для повторення формул скороченого множення (квадрат суми, квадрат різниці, різниця квадратів, сума кубів, різниця кубів), так і практичні завдання на пошук помилки у записі формули, на відновлення многочлена, застосування формул для розв’язування нестандартних вправ таких як розв’язування рівнянь і вправи на подільність.
Для зацікавлення учнів поданий матеріал прикладів софізму із застосуванням формул скороченого множення, а також історична довідка. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
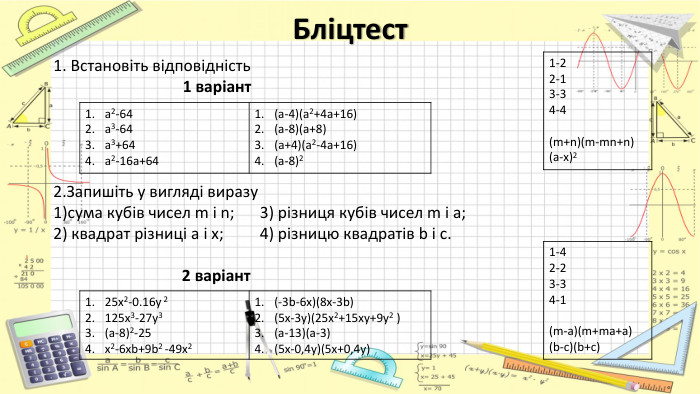
Застосування різних способів розкладання многочлена на множники Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку