Презентація "Висота, бісектриса та медіана трикутника"
Про матеріал
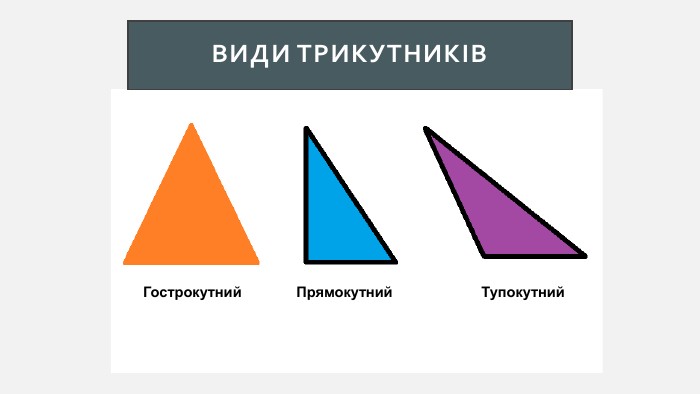
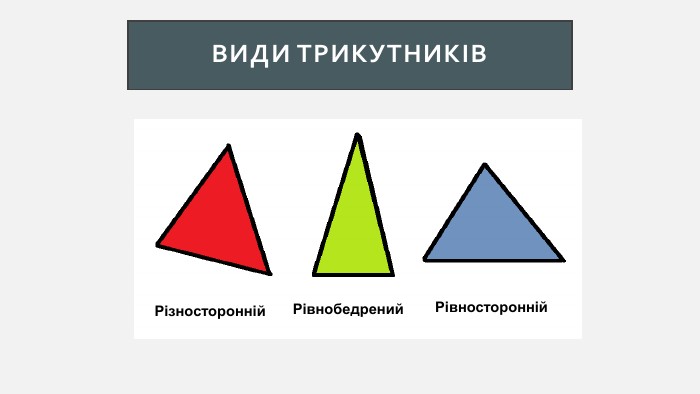
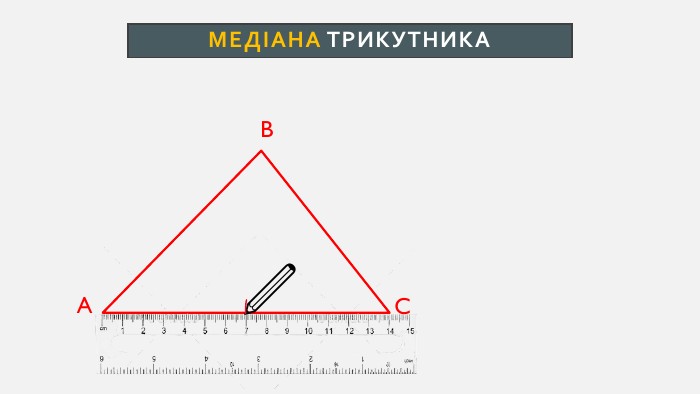
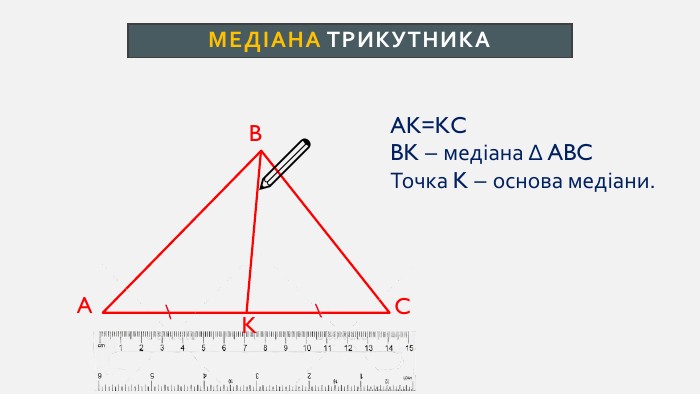
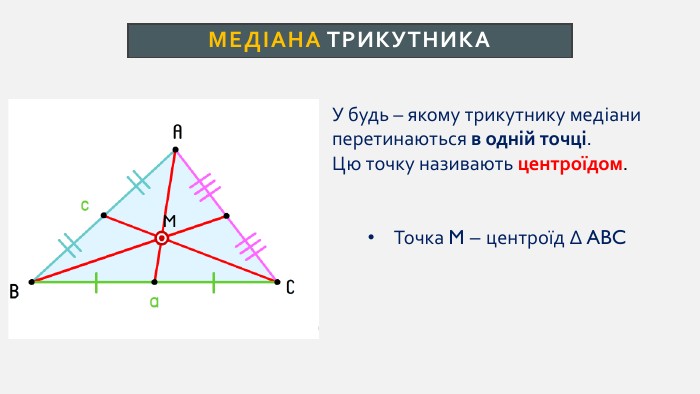
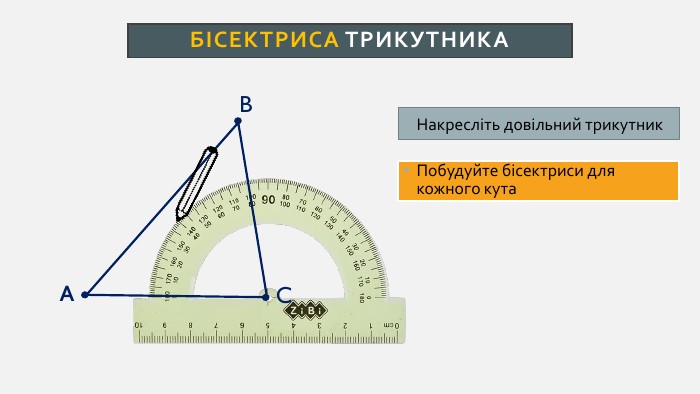
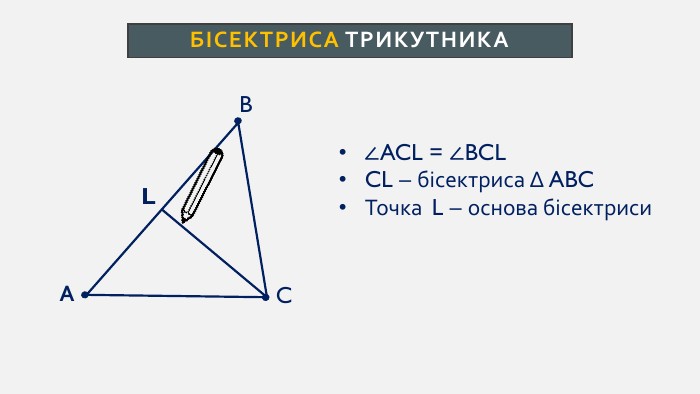
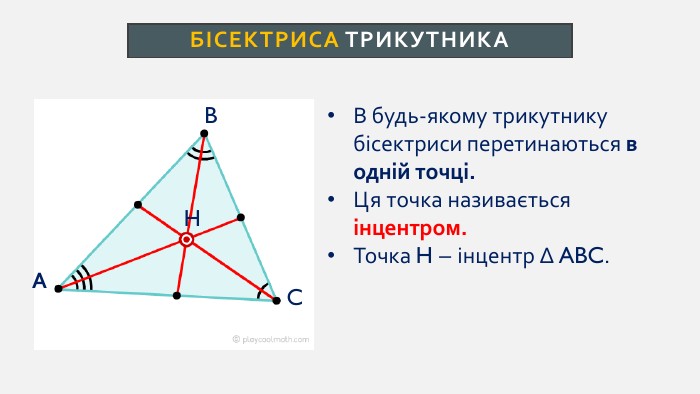
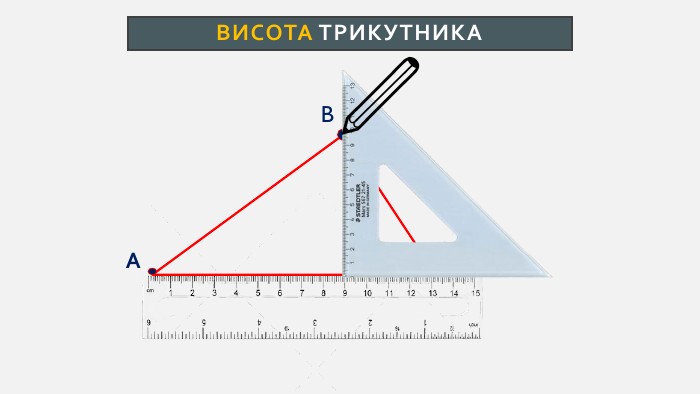
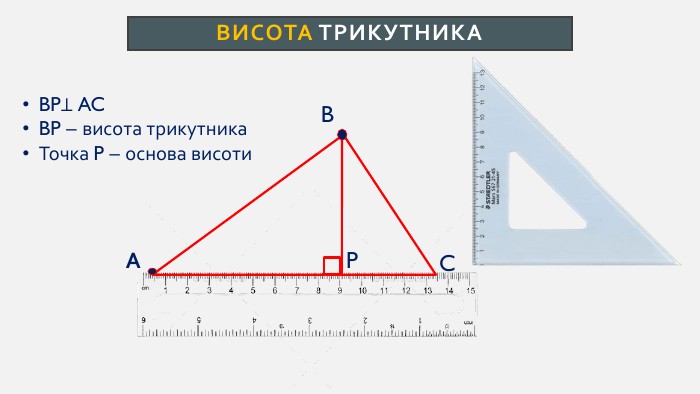
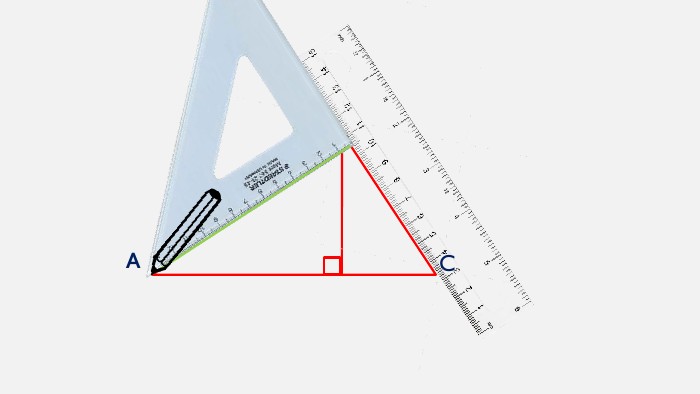
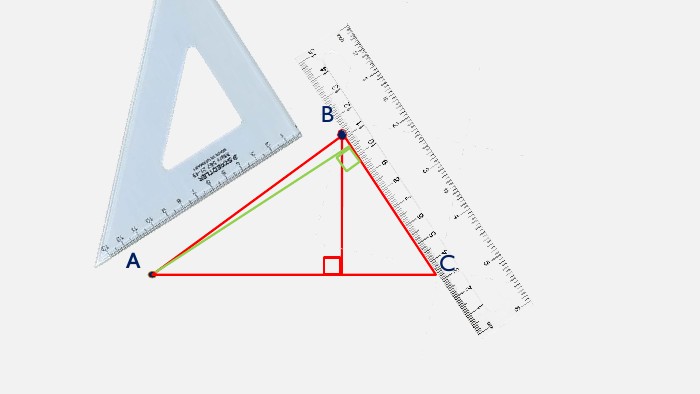
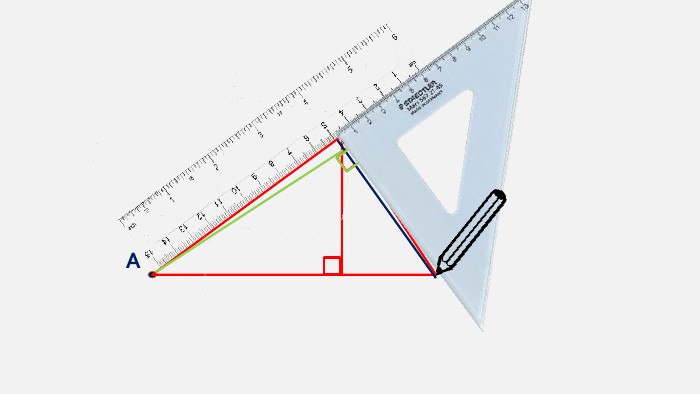
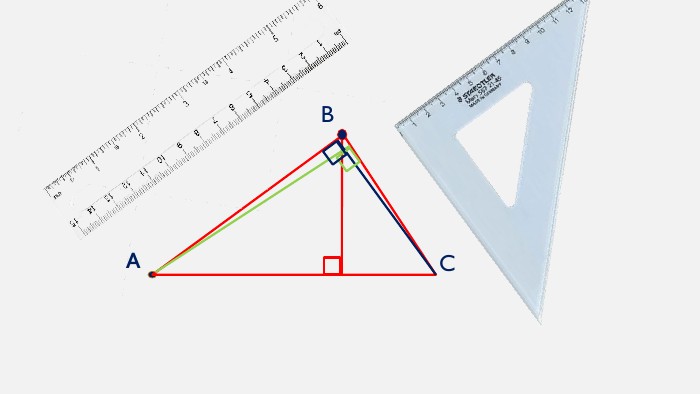
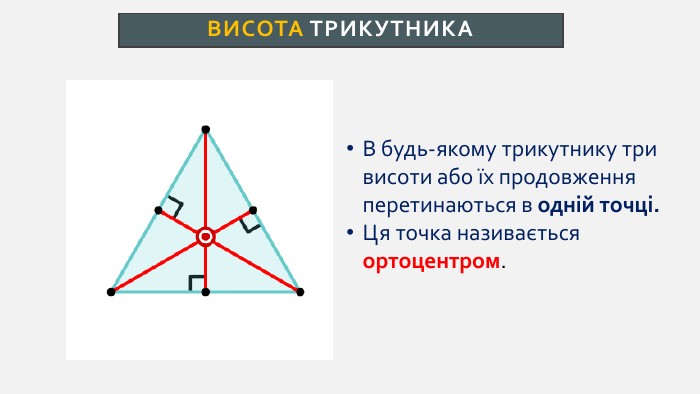
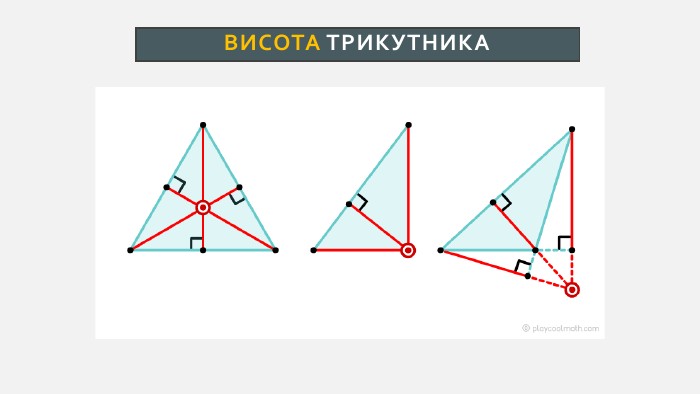
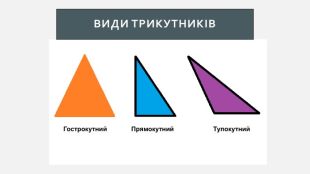
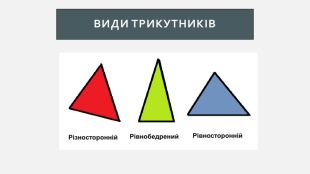
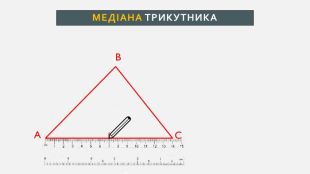
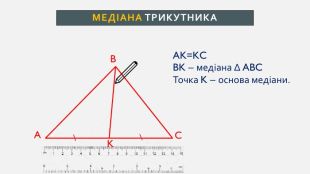
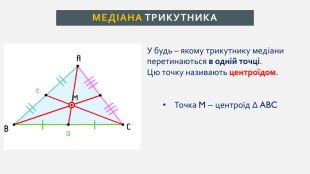
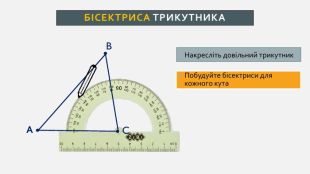
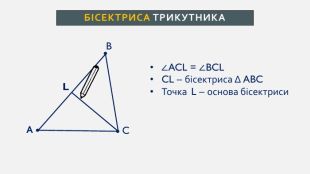
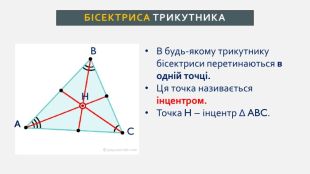
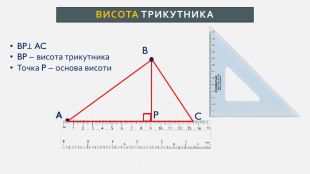
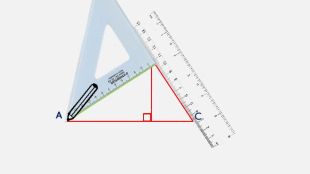
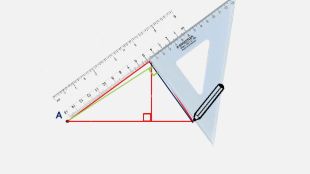
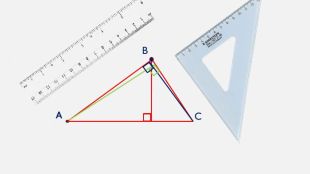
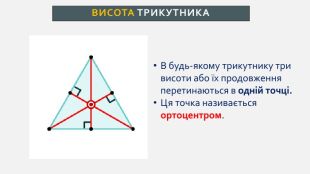
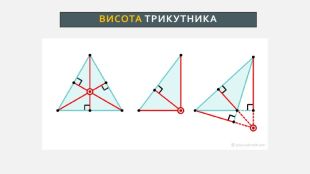
Презентація створена для проведення уроку геометрії в 7 класі. Знайомимо учнів із поняттями: медіана, бісектриса, висота трикутника; формулюємо вміння зображувати ці відрізки.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку