Проект для учня 5 класу " Історія звичайних дробів"

 

Історія звичайних дробів

Валентина 1.6.2020

                        Зміст

 

1.   Вступ…………………………………………. 2
2.   Стародавній Рим……………………………...3
3.   Стародавній Єгипет…………………………..4
4.   Вавилон………………………………………. 5
5.   Стародавня Греція…………………………....6
6.   Київська Русь………………………………... 7
7.   Індія………………………………………….. 7
8.   Дроби в інших державах давнини…………. 8
9.   Стародавні задачі з дробами………………. 10
10.                 Цитати про дроби…………………………13
11.                 Висновки…………………………………..14
12.                 Список використаної літератури………...15

 

 

 

 

 

 

 

 

 

 

                        Вступ

      Необхідність в дробових числах виникла на ранній стадії розвитку людини. Разом з необхідністю рахувати предмети з давніх часів з’явилася потреба вимірювати довжину, площу, об’єм,час і інші величини. Результат таких вимірів не завжди вдається виразити натуральним числом, доводиться враховувати і частини міри, що використовуються. Історично дроби виникли в процесі вимірювань.

 Об’єкт дослідження:
Історія виникнення звичайних дробів
Предмет дослідження :
Звичайні  дроби
Методи дослідження :
- робота з літературою
- пошук інформації у всесвітній мережі  інтернет
- робота з дробами
Мета роботи:
-розширення знань про виникнення дробів
-вивчення послідовності удосконалення записів звичайних дробів.

     Завдання дослідження:

• знайти і вивчити інформацію  з  даної  теми;
• вибрати і впорядкувати матеріал ;
• розглянути стародавні задачі з дробами;
• знайти шляхи розв’язання стародавніх задач з дробами;
• систематизувати одержані знання, зробити висновок.

Актуальність: 

-  вже в дитинстві людина  використовує не тільки цілі предмети, але і  їх  частини;

  - у шкільних підручниках немає інформації про історію виникнення дробів. А навіщо вивчати дії з дробами, якщо ми не знаємо, чи потрібні вони нам?

 

 

                                Стародавній Рим

Цікава  система дробів була в  Стародавньому Римі. Вона була заснована на діленні на 12 частин одиниці ваги, яка називалася асс. Дванадцяту частину асса  називали унцією.  А шлях, час і інші величини порівнювали з наочною річчю - вагою. Наприклад, римлянин міг сказати, що він пройшов сім унцій шляху  чи  прочитав  п’ять унцій книги. При цьому, звичайно,  мова  йшла не  про зважування  шляху  чи  книги. Мали на увазі, что пройдено 7/12  шляху  чи прочитано  5/12 книги

 

                                                         "скрупулус " - 1/288 асса,

                                                                  "семис" - половина асса,

                                                                 "секстане" - шоста  частина асса,

                                                                "семиунція" -  1/24 асса  і т.д.

 

1 тройська  унція золота — міра ваги  дороговартісних металів

 

 

                                                                   

 

            Стародавній Єгипет

    У Стародавньому  Єгипті  архітектура  досягла  високого рівня.  Для того, щоб  будувати  грандіозні  піраміди  і  храми , щоб  обчислювати  довжини,  площі  і  об’єми  фігур, необхідно було знати арифметику.

   Із розшифрованих  даних  на папірусах  вчені  взнали, що єгиптяни  4 000 років  назад  вміли розв’язувати  багато  задач, пов’язаних з будівництвом, торговлею  і  військовою  справою.                                                                Єгиптяни використовували тільки дроби з чисельником одиниця, тобто  дроби виду 1/n. Єдиним винятком був дріб 2/3. Вони всі дроби намагалися записати як суми частин.                                                                                             Додавали, віднімали, ділили і множили дроби за допомогою спеціально складених таблиць, які доводилося завчати.

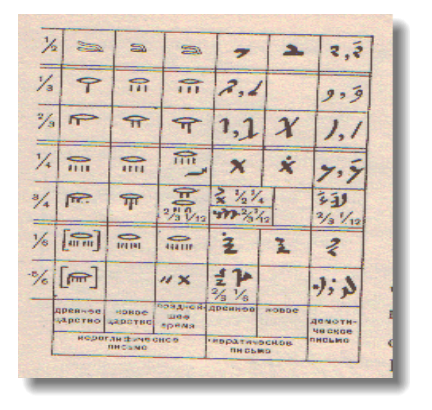
                        Вавилон

У давньому  Вавилоні  високий рівень культури  був  досягнутий  у третьому тисячолітті  до нашої  ери.  Тоді  писали не на папірусі,  який  у країні  не ріс, а на глині.  Натисканням  клиновидної  палички  на  глиняні  дощечки наносилися  знаки,  що мали  вигляд  клинів, потім вони випалювалися  на вогні. Ось  чому таке письмо називається  клинописом. Вавилоняни  користувалися  всього двома цифрами. Вертикальна  риска  означала одну одиницю, а  кут між двома похилими рисочками – десять..

Вони  працювали тільки з  дробами, в яких знаменник число 60, а такі дроби, як 1/7, 1/11, 1/13 не можна було точно виразити через шістдесят: виражали їх наближено. Шестидесятковими дробами, успадкованими від  Вавилону,  користувалися  грецькі  і арабські математики і астрономи. Ми   зараз використовуємо такі дроби,  щоб виразити час  і величину кутів.

 

 

  

              Стародавня Греція

    У  грецьких  творах  з математики  дробів  не  було. Грецькі  вчені  рахували, що математика  має  займатися тільки  цілими числами.                                           З дробами  доводилося  мати справу купцям, ремісникам, а також  землемірам, астрономам і механікам. «Якщо  ти  захочеш  ділити  одиницю,  математики висміють  тебе і не  дозволять  це  робити», -  писав  засновник  афінської академії  Платон.  Але  стара  приказка  говорить: « Жени природу в двері,  вона влетить  в вікно».  Тому  і  в  наукових  творах  греків  з’явилися дроби.   Оскільки греки працювали зі звичайними дробами лише епізодично, вони використовували різні позначення. Герон і Діофант, найбільш  відомі арифметики серед  давньогрецьких математиків, записували дроби в алфавітній  формі, причому  чисельник  розташовували під знаменником. Ще за 2-3 століття до Евкліда і Архімеда греки вільно володіли арифметичними діями  з дробами.   В VI ст. до н.е. жив відомий вчений Піфагор.                Кажуть, що на питання, скільки учнів відвідують його школу, Піфагор відповів: «Половина вивчає математику, четвертина – музику, сьома частина перебуває в мовчанні».

 

 

 

                                       Київська  Русь

У  староруських  рукописних арифметиках XVII століття дроби називали долями, пізніше «ломаними числами». В старих рукописах знаходили такі назви дробів на Русі:

 

1/2 - половина, полтина	1/3 – треть
1/4 – четь	1/6 – півтреть
1/8 - півчеть	1/12 –півпівтреть
1/16 - півпівчеть	1/24 – півпівпівтреть (мала треть)
1/32 – півпівпівчеть (мала четь)	1/5 – пятина
1/7 - седьмина	1/10 - десятина

 

                   Індія

Математики цієї країни  змогли  досить  щвидко  перейти  від одиничних дробів  до  дробів  загального  вигляду.  Вперше такі  дроби  зустрічаються в «Правилах веревки» Апастамби (VII-V ст. до н.е.),  які  містять геометричні побудови  і  результати  деяких   обчислень. В  Індії  використовувалась система запису –  можливо, китайського, а  можливо, пізньогрецького походження, – при  якій  чисельник  дробу  писали  над знаменнком –  як  у нас,  але  без риски дробу, зате  весь  дріб  вміщувався  в прямокутну  рамку.

Іноді  використовувався  і «трьохповерховий» вираз  з трьома  числами  в одній рамці; в залежності  від  контексту  це  могло означати  неправильний дріб  (a + b/c)  чи  ділення  цілого числа a на дріб b/c.
Наприклад,  дріб   записували  як
2
1
5

Правила дій  з  дробами,  викладені  індійським  вченим Брамагуптой (VIII ст.),  майже  не відрізнялися  від  сучасних.  Як  і  в  Китаї, в  Індії  для зведення  до  спільного  знаменника  довгий  час  перемножали знаменники всіх  доданків,  але  з  IX ст. користувалися  вже  найменшим  спільним кратним.

          Сучасну систему запису дробів створили в Індії. Тільки там писали знаменник зверху, а чисельник знизу, і не писали риску дробу. Правила дій над дробами майже не відрізнялися від сучасних. А у  індійського математика Брамагупти знаходимо досить розвинуту систему дробів. Чисельник і знаменик записуються так  як і в нас зараз, тільки без горизонтальної риски, а просто разміщені один над другим.

 

Дроби в інших державах давнини

Араби першими почали відокремлювати рискою чисельник  від знаменника.

Вони почали записувати дроби так, як ми це робимо сьогодні.

Араби користувалися трьома системами записів дробів:

• Як в Індії: записували знаменник під чисельником; дробова риска з’явилася  в кінці XII – на початку XIII ст.
•  чиновники, землеміри, торговці користувалися   дробами, схожими на єгипетські, при цьому використовували дроби  зі знаменниками, які не перевищували 10 (тільки для таких дробів арабська мова мала спеціальні терміни); часто використовували  наближені  значення; арабські вчені  працювали над  вдосконаленням  цього числення.
• Арабські  вчені  успадкували  вавилонсько-грецьку шестидесяткову систему, в якій, як і греки, використовували  алфавітний запис, поширивши  його  і на цілі частини.  

У  Китаї практично всі  арифметичні  операції  зі звичайними дробами були  відомі  вже до II століття до н. е.;  вони описані в фундаментальній збірці  математичних знань давнього Китаю – «Математика  в дев’яти книгах»,  кінцева  редакція  якої  належить  Чжан Цану.

       Китайські математики скорочували дроби. Множення  дробів виконували  як  обчислення  площі  прямокутної  земельної  ділянки, довжина  і ширина  якої  виражені  дробовими числами. Ділення  розглядали за  допомогою  ідеї  поділу, при якому  китайських математиків  не  бентежило, що число  учасників  поділу  може  бути дробовим, наприклад,  3⅓  людини.

Спочатку  китайці  використовували  найпростіші  дроби,  які  одержували  назви    використанням  ієрогліфа бань :
бань («половина») –1\2;
шао бань («мала половина») –1\3;
тай бань («велика половина») –2\3.

 

 

У Західній Європі вперше термін «дріб» вжив Леонардо Пізанський в 1202році ( Фібоначчі).Він став використовувати риску дробу, записує дроби, розміщуючи у випадку мішаного числа, цілу частину справа, але читає так, як прийнято у нас. Спочатку європейські математики оперували тільки зі звичайними дробами. Повноцінна теорія звичайних дробів і дій з ними склалася в XVI столітті, завдяки італійському ученому Нікколо Тарталья і німецькому математику Клавіусу. Назви чисельник  і знаменник ввів в 13 столітті Максим Плануд – грецький монах, вчений, математик.

      Стародавні задачі з дробами

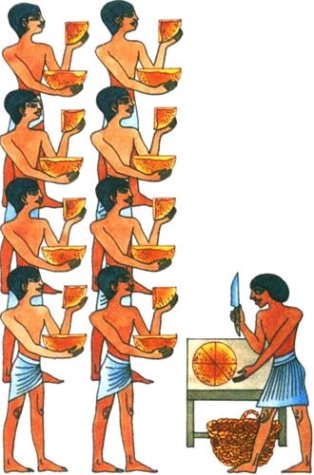
1. У Папірусі Ахмеса є така задача— розділити 7 хлібин між 8 людьми  порівну.

Сучасний школяр  розв’язував би задачу так: треба розрізати кожну хлібину на 8 рівних частин і кожній людині дати по одній частині від кожної хлібини.

А ця задача  на папірусі розв’язана так :

      Кожній людині треба дати по половині, четвертині і восьмій частині хліба.   Тепер зрозуміло, що треба 4 хлібини розрізати наполовину, 2 хлібини на 4 частини і тільки один хліб – на 8 частин.                                         Якщо нашому школяреві треба зробити 49 розрізів, то Ахмесу – всього 17, тобто єгипетський спосіб майже в 3 рази економніший.

 

 

2)Задача Горація (I ст. до н.е.)

Учитель. Нехай скаже син Альбіна, скільки залишиться, якщо від п’яти унцій відняти одну унцію?

Учень. Одна третя.

Учитель. Правильно. Ти зможеш зберегти своє майно.

Розв’язання:                 

                 4 унції                                     4 унції                              4 унції

 

Відповідь: 1/3

3) Задача із "Папіруса Ахмеса"

(Єгипет, 1850 р. до н. е.)

Приходить пастух з 70 биками.

Його питають:

 - Скільки приводиш ти свого багаточисельного стада?

Пастух відповідає:

 - Я привів  дві третіх від третини худоби. Порахуй!

Розв’язання:                 

1) 70:2·3=105 (голів) - це 1/3 від тварин

2) 105·3=315 (голів)  худоби

   Відповідь: 315 голів худоби.

4)Задача із "Арифметики"
Мухамеда ібн-Муси  аль-Хорезми
(IX ст.  н. е.)

Знайти  таке  число, що  якщо  відняти  від  нього одну третю  і одну четверту, то отримаємо 10.

Розв’язання:                 

 

четвертина                                 третина                             число 10

 

                - відняли від числа два рази

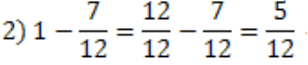              - становить число 10

                - шукане число

Відповідь: 24

5) Задача Вірменського вченого

Ананія Ширакаци (VII ст.  н.е.)

Один купець  пройшов  через  3  міста,  і  брали  з  нього  в першому  місті податок  половину  і  третину  майна,  і  в  вдругому  місті  половину і  третину  (з того, що  залишилось),  і  в третьому  місті   половину і  третину  (з  того, що  залишилось). Коли  він  прибув  додому,  у  нього  залишилось 11 грошових  одиниць. Скільки  всього грошей  було  спочатку  в  купця?

Розв’язання:

                                                   –  становить  майно  взяте  в III місті;

 

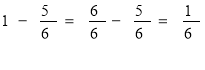
                                                   –  це 11 грошових

одиниць;

11 • 6 = 66  –  було у купця  в III місті;

66  грошових одиниць  становить   частина,що залишилася  в II місті;

66 • 6 = 396  – грошових одиниць  було в  другому  місті;

396 – грошових одиниць   становить   частина,що залишилася  в  I місті;

396 • 6 = 2376  –  грошових одиниць   було в  купця  спочатку.

Відповідь: 2376 грошових одиниць .

           Цитати про дроби

                                                                                                                                                                   Ціцерон говорив: «Без знань дробів ніхто не може говорити,що знає арифметику».

 

 

 

 

 

«Людина подібна дробу, чисельник якої є те, що людина  представляє собою, а знаменник – те, що вона думає про себе. Чим більшої думки про себе людина, тим більший знаменник, а значить - менший дріб».

                                            Л.М.Толстой

 

                                             Висновки:

Вчення  про дроби  вважалось  найскладнішим розділом математики  у всі часи  і у всіх народів. Хто знав дроби, був  в пошані. Автор старовинного  слов’янського рукопису  XV ст. пише: «Не є  це диво, що …в цілих, але  є похвальним ,  що в частинах…».

Зроблено  висновок,  що історія  звичайних дробів – це  хвиляста  дорога  з багатьма перепонами  і  труднощами. Розділ арифметики про дроби довгий час  був один з найбільш складних. Недарма у німців збереглася приказка: «Попасти в дроби», що означало – зайти у безвихідне становище. Вважалося, що той хто не знає дробів, не знає арифметики. Під час  роботи  я взнала багато нового і цікавого. Прочитано  багато книг і розділів з енциклопедії. Познайомилась з першими дробами,  якими оперували люди,  взнала нові для мене  імена вчених, які  внесли  свій вклад в развиток  вчення про дроби. Сама спробувала розв’язувати  цікаві задачі, самостійно підбирала  старовинні задачі, розбирала розв’язки  наведених в текстах  задач. Відповідь на питання, яке я задала собі перед початком работи  над дослідженням: звичайні  дроби необходні, вони важливі. В стародавніх джерелах зутрічаються дроби.

             Записувати дроби за допомогою чисельника і знаменника стали в Стародавній Греції.                                                                                                                  Сучасне позначення дробів бере  початок  у стародавній Індії. Його використовували араби, а потім у XII—XIV ст. запозичили європейці. Спочатку дроби записували без дробової риски;  пізніше дробову частину стали писати чорним чорнилом або відділяти вертикальною рискою. Риску дробу почали застосовувати близько 300 років тому.

 

 

 

 

 

 

 

 

 

Список використаної літератури

• Бородін А.і. Із історії арифметики. Головне видавництво «Вища школа»-К.,1986
•  «Велика енциклопедія Кирила і Мефодія» /В. М. Карєв,  2005р.-1136с
• Г.І.Глейзер “Історія математики в школі :IV-VI кл. ”- М.: Просвещение,1981р.
• Енциклопедія для дітей. Аванта+, 1999р.- 588с
• І.Я. Депман, Н.Я. Віленкін «За сторінками підручника математики» М.   «Просвещение»1989.- 286с
• Математика: підруч. для 5 класу загальноовіт. навч.закл./Н.А Тарасенкова, І.М.Богатирьова, О.П.Бочко, О.М.Коломієць, З.О.Сердюк.-К.: Видавничий дім «Освіта», 2013. – 352с

     Інтернет - ресурси:

• http://www.uroki.net/docnach/docnach39.htm
• http://festival.1september.ru/articles/410393/ 
• http://wiki.saripkro.ru/index.php/Навчальний_проект_Звичайні _дроби 
• http://botinok.co.il/node/21854