Рівняння з двома змінними

Рівняння з двома змінними Підготувала вчитель математики. Городянської гімназії Стефурак Галина Василівна. Алгебра

Рівняння – це не просто рівність. З одною змінною чи кількома. Рівняння – це думок активність. Це інтелекту боротьба. То ж будьте творчими, активно розвивайтесь. Долайте труднощі у своєму житті,Але з рівняннями, прошу не розлучайтесь. Вони послужать вам ще в майбутті Л. О. Буката

Приклад. Нехай потрібно знайти два числа, сума яких дорівнює 10. Рівність х+у=10 містить дві змінні х і у. Така рівність називається рівнянням з двома змінними або рівнянням і двома невідомими. Наприклад: х+4у=45; 2х-4у+3ху=8; 2х2+у=8 Якщо перше число позначити буквою х, а друге буквою у, то відношення між ними можна записати у вигляді рівності х + у = 10.

Приклади деяких ситуацій. Складемо математичну модель задачі.1. Площа квадрата, сторона якого – 10 см, дорівнює двох інших квадратів. Площа квадрата зі стороною 10 см дорівнює 100 см2. Якщо довжини сторін двох інших квадратів позначити х см і у см, то отримуємо рівність х2 + у2  = 100. 2. Купили 5 ручок і 7 зошитів. За всю покупку заплатили 41 грн. Якщо одна ручка коштує х грн, а один зошит – у грн, то можна записати у вигляді рівності 5х + 7у = 41

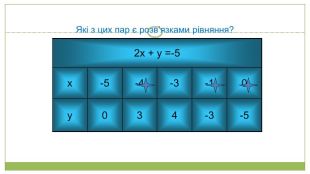
В рівнянні х + у =10 якщо х=2, у=8, то дістанемо рівність 2+8=10. Говорять, що пара значень х=2, у=8 є розв'язком рівняння х+у=10.Є інші розв’язки. Наприклад, якщо х=4, у=6, то 4 + 6 = 10. Пара значень х=3, у=8 не перетворює рівняння х+у=10 на правильну рівність. У такому разі гово­рять, що пара значень х=3, у=8 не є розв'язком рівняння х+у=10.

Розв'язком рівняння з двома змінними називається пара значень змінних, які перетворюють це рівняння на правильну рівність. Наприклад, пара чисел х=3 і у=4 є розв’язком рівняння х2+у2=25, а записують так (3;4) а пара чисел (-3;-1) — розв’язком рівняння ху=3. Кожна з пар чисел (40;50), (50;40), (5;85), (10;80) і т.д. є розв’язком рівняння х+у=90. Їх є безліч. Рівняння х+у = 0 має один розв’язок – (0;0). Рівняння х2+у2=−2  взагалі не має розвязків, бо сума двох невід’ємних чисел не може дорівнювати від’ємному числу. Розв’язати рівняння з двома змінними – це означає знайти всі його розв’язки або показати, що їх немає.

Щоб знайти розв’язки рівняння з двома змінними, слід підставити в рівняння довільне значення однієї змінної і, розв’язавши утворене рівняння, знайти відповідне значення іншої змінної Наприклад. Знайдемо кілька розв’язків рівняння 3х-у=5. Якщо х=1, то 3∙1-у=5, звідси у=-2. Пара чисел (1;-2)- розв’язок даного рівняння. Якщо х=2, то 3∙2-у=5, звідси у=1. Розв’язок - (2;1). Їх є безліч. Наприклад . Розв’яжемо рівняння (х−3)2+у2=0 Сума двох виразів дорівнює нулю, тільки за умови, коли х-3=0 і у=0. Отже рівняння має один розв’язок - (3;0). 

Рівняння з двома змінними, які мають ті самі розв'язки, називаються рівносильними. Рівняння, які не мають розв'язків, теж називають рівносильними. Рівняння з двома змінними мають ті самі властивості, що й рівняння з однією змінною.-В рівнянні можна розкрити дужки або звести подібні доданки;- у рівнянні з двома змінними доданки можна переносити з однієї частини рівняння до другої, змінивши знаки цих доданків;обидві частини рівняння можна помножити або поділити на те саме відмінне від нуля число. При цьому дістанемо рівняння, рівносильне даному.

Приклад 1. Чи має розв’язки рівняння:1) у𝟐=х𝟐;𝟐)х 𝟐+у𝟐=𝟐𝟓; 3)х𝟐+у𝟐=−𝟐𝟓; 4)х+у=𝟏 1) 02=02. Отже, рівняння у2=х2 має, наприклад, розв′язок 0;0;2) 3 2+42=25; 9+16=25.  Отже, рівняння  х 2+у2=25  має, наприклад, розв′язок 3;43) рівняння  х 2+у2=−25  не має розв′язків, бо сума невід’ємних чисел не може дорівнювати від’ємному числу;4) 1+0=1; 1=1. Отже, рівняння х+у=1 має, наприклад, розв’язок (1;0) 

Приклад 2. Скільки розв’язків має рівняння: 𝟏)х𝟐+ (у−𝟐)𝟐=𝟎; 2) 𝟗х𝟐+ 𝟏𝟔у𝟐=𝟎;𝟑) (х𝟐+ у𝟐)у=𝟎; 𝟒) х𝟐+у=0; 5) х+у=2? Розв’язання1)Сума невід’ємних чисел  х2+ (у−2)2=0 може дорівнювати нулю лише тоді, коли кожне з них дорівнюватиме нулю. Тобто х=0 і у-2=0; х=0 і у=2. Отже пара чисел (0;2) – єдиний розв’язок рівняння  х2+ (у−2)2=0; 2) рівняння 9х2+ 16у2=0 має єдиний розв′язок −0;0;3) рівняння (х2+ у2)у=0 має безліч розв’язків, у яких – х –будь-яке число, а у=0;4) рівняння 4) х2+у=-100 не має розв’язків, бо сума невід’ємних чисел не може дорівнювати від’ємному числу; 5) рівняння х+у=2 має безліч розв’язків. 

Приклад 3. Чи проходить через початок координат графік рівняння: 1) х2−ху+2=0; 2) х3−4у=х2+3х. Розв’язання Підставимо координати початку координат (0;0) у рівняння1) 02−0∙0+2=2≠0. Отже, графік рівняння х2−ху+2=0 не проходить через початок координат.2) 03−4∙0=02+3∙0=0.  Отже, графік рівняння                                         х3−4у=х2+3х  проходить через початок координат. 

Приклад 4. Чи належить графіку рівняння 2х2–у+1=0 точка : 1) А(-3;-17); 2)В(2;9); 3)С(-2;9); 4)D(-1;4)? 2∙(−3)2-(-17)+1=18+17+1=36≠0. Отже, точка А(-3;17) не належить графіку рівняння 2х2–у+1=0;2∙22-9+1=8-9+1=0. Отже, точка В(2;9) належить графіку рівняння 2х2–у+1=0;2∙(−2)2-9+1=8-9+1=0. Отже, точка С(-2;9) належить графіку рівняння 2х2–у+1=0;2∙(−1)2-4+1=2-4+1=−1≠0. Отже, точка D(-1;4) не належить графіку рівняння 2х2–у+1=0. 

Приклад 5. Графік рівняння 4х+3у=30 проходить через точку А(6;b). Чому дорівнює b?Розв’язання. Підставимо значення х=6 та у=в у рівняння, матимемо:4∙6+3∙b=30;24+3b=30;3b=6;b=2. Відповідь: 2 

Приклад 6. Знайдіть двоцифрове число, яке у 2,5 раза більше за добуток його цифр. Розв’язання. Двоцифрове число ху=10х+у, добуток його цифр х∙у більше у 2,5 рази. Маємо рівняння: 10х+у=2,5(х∙у);10х=2,5ху-у;10х=у(2,5х-1);2,5х-1 повинно бути цілим і дільник 10, тобто х=2. Якщо х=2, то 20=у∙4; у=5. Відповідь:25 

Приклад 7. Розв’яжіть рівняння х2+у2+1=2х; Розв’язання. Використовуючи властивості рівнянь з двома змінними, перетворимо дане рівняння на рівносильне. Перенесемо 2х у ліву частину, помінявши знак на протилежний.х2+у2+1=2х;х2−2х+1+у2=0;Погрупувавши, використаємо формулу скороченого множення квадрат різниці (х2−2х+1)+у2=0;                            (х−1)2+ у2=0;Сума невід’ємних чисел може дорівнювати нулю лише тоді, коли кожне з них дорівнюватиме нулю. Тобто (х−1)2=0 та у=0; х=1 і у=0. Відповідь: (1;0) 

Які з даних рівнянь є рівняннями з двома змінними?x+у+z=0;2) xy+1=2; 3)5m-3n=6;4) а - 3b=8c;6)х3-8xy=100. 5)2х-7=5х;

Які з цих пар є розв’язками рівняння?2х + у =-5х-5-4-3-10у034-3-5

Творче завдання. Складіть рівняння із двома змінними, розв’язком якого є пара чисел (-2;3). Доберіть замість зірочок такі числа, щоб пари (3; * ) і (*; 2) були розв’язками рівняння 5х -2у = 9.

До наступної зустрічі!

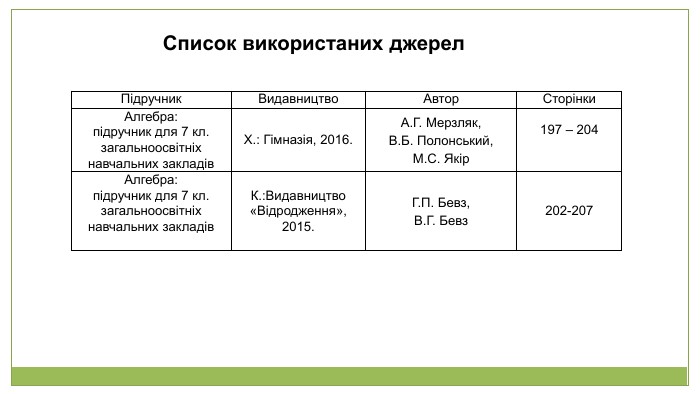
Список використаних джерел {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Підручник. Видавництво. Автор. Сторінки. Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Х.: Гімназія, 2016. А. Г. Мерзляк,В. Б. Полонський,М. С. Якір197 – 204 Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів К.: Видавництво «Відродження», 2015. Г. П. Бевз,В. Г. Бевз202-207

Графічний диктант (Так , ні__.)Чи є правильними твердження? 1. Рівняння 2/х = 4 є лінійним.2. Рівняння 2х=-0,5 має один корінь.3. Рівняння 5х+3=5х має безліч коренів.4. х2-1 =0 не є лінійним.5. Рівняння 5х+25=5(х+5) не має коренів.6. Число –1 є коренем рівняння -х-6=-5 . Ключ-відповідь: