Розкладання многочленів на множники способом винесення спільного множника за дужки та способом групування.
РОЗРОБКА УРОКУ З АЛГЕБРИ В 7 КЛАСІ З ТЕМИ «РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ СПОСОБОМ ВИНЕСЕННЯ СПІЛЬНОГО МНОЖНИКА ЗА ДУЖКИ ТА СПОСОБОМ ГРУПУВАННЯ».
Тема: Розкладання многочленів на множники способом винесення спільного множника за дужки та способом групування.
Мета: Систематизувати вміння учнів в перетворенні многочленів в добуток;
формувати навички самостійної роботи, розвивати творчі здібності;
навички роботи в групі.
Тип уроку: урок засвоєння навичок і вмінь.
Обладнання: роздавальний матеріал для “математичного лото”.
ХІД УРОКУ
- Організаційний момент.
Підготовка дошки. Провітрювання кімнати. Привітання.
-
Перевірка домашнього завдання
- Чотири учні на дошці розв'язують вправи
|
Розкласти на множники: |
|||
|
ax+3+3x+a= |
5a-10+ac-2c= |
2am+3mx-7m-2ac-3cx+7c= |
x²+6x+5= |
- Учитель перевіряє наявність домашнього завдання в учнівських зошитах.
- Опитування.
- Які вирази називаються многочленами?
- Що означає розкласти многочлен на множники?
- Способи розкладання многочлена на множники?
- Як розкласти многочлен на множники способом групування?
III. Мотивація вивчення теми.
При перетворенні цілих алгебраїчних виразів виникає необхідність подати многочлен у вигляді добутку одночлена та многочлена, двох або більше многочленів. Виконання таких перетворень вимагає вмінь передбачити результат, застосовувати нестандартні прийоми.
IV. Узагальнення та систематизація вивченого матеріалу.
1. Розклади на множники (усно):
a(x-2)+(x-2)=
c+d-4(d+c)=
3(b-5)-a(5-b)=
m-n+(m-n)y=
- Гра “Математичне лото”
Учні об’єднуються групи, кожна з яких отримує картку з записаними відповідями та умови завдань на окремих картках.
Учні розв'язують завдання й накривають відповідні відповіді.
Картка №1
|
3a²(1-2a) |
c(c-9)(c-1) |
(a-2c)(6-p) |
|
(2x+7)(x-4) |
(2-3a)(a-2b) |
(x-y)(-y-2x) |
|
(y²+1)(y-6) |
(x²-2)(x-14) |
mn³(m²-6n) |
Картка№2
|
(x-y)(x+2) |
(a+2)(4a-7) |
(b²+1)(b-5) |
|
(a-b)(5-2a+2b) |
x(x-3)(5-x) |
(7-c)(c²+1) |
|
8y(1-4y) |
(3-n)(a+1) |
6a²(2 - a) |
Картка №3
|
5x²(3x-1) |
(x-4y)(7-5x) |
(2xy-3z)(5y+xz) |
|
(b-1)(a-4) |
(3x-1)(2m+3) |
(2-b)(1+b²) |
|
(3b-2c)(2x-1) |
mn²(m-3n) |
(7-a)(a²+1) |
Завдання до карток.
Розкладіть многочлени на множники:
|
№1 |
№2 |
№3 |
|
1) 12a²-6a³= |
1) 15x³-5x²= |
|
2)3a+3- n a - n= |
2) 6mx-2m+9x-3= |
|
3) a(4a-7)+2(4a-7)= |
3) 7(x-4y)²-5x²+20xy= |
|
4) 5(a-b)-2(a-b)²= |
4) 2x(3b-2c)-3b+2c= |
|
5) 5x(x-3)-x²(x-3)= |
5) a(b-1)-4b+4= |
|
6) 8y-32y²= |
6) m²n³ - 3mn²= |
|
7) x(x-y)+2(x-y)= |
7) 7a²+7-a³-a= |
|
8) 3a-15+ax-5x= |
8) 2+2b²- b-b³= |
|
9) 7c²- c³-c+7= |
9) 2x²yz-15yz-3xz²+10xy²= |
Учні записують розв’язання в зошити і накривають відповідь карткою(на звороті кожної картки буква). Розв’язавши всі завдання, учні одержують слово – «творчість». Обговорюються підсумки гри.
V. Навчальна самостійна робота.
|
Середній рівень |
Достатній рівень |
Високий рівень |
|
1) Розкладіть на множники: a² - ab - 8a + 8b |
1) Розкладіть на множники: x³-3x²+5x-15 |
1) Розкладіть на множники: x2- 7x - 8 |
|
2) Розв’яжіть рівняння: y(y+2)-7(2+y)=0 |
2) Розв’яжіть рівняння: 3x2- 9x - x+3=0 |
2) Розв’яжіть рівняння: x³-5x²+x=5 |
Вчитель корегує виконання вправ, аналізує типові помилки.
Учитель підкреслює, що завдання виконувались за відомими алгоритмами розкладання многочленів на множники. Але окремі завдання вимагають нестандартного, творчого підходу.
Учень на дошці демонструє розв’язання домашнього творчого завдання: Розкласти на множники ![]() .
.
Розв’язання.
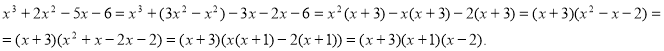
VІ. Підсумок уроку.
Я знаю…
Я вмію…
Мені сподобалось
VІІ. Домашнє завдання
№ 568 (а – в), № 564(б); творче завдання № 581(в).


про публікацію авторської розробки
Додати розробку
