Розробка "Туристична геометрія"

              ТУРИСТИЧНА  ГЕОМЕТРІЯ

 

    У польових умовах туристичних походів часто виникає потреба встановити відстані чи розміри об’єктів без застосування вимірювальних приладів,  на основі окомірних визначень та математичних розрахунків.

      У розробці, яка підготовлена за матеріалами наукових  видань,  зібрана і систематизована інформація про найпростіші способи  геометричних вимірювань на місцевості.

    Запропоновані матеріали можуть бути використані  вчителями географії  на уроках, факультативних та гурткових заняттях, керівниками туристичних клубів під  час організації  походів. 

 

                                      Вступ

 

       Туристичні походи ваблять романтикою  і новизною відкриттів мільйони людей. Та, щоб уникнути труднощів і несподіванок під час подорожей, треба вміти читати не всім зрозумілу книгу природи. Великою мірою успіх походу залежить від уміння орієнтуватися на місцевості, обрати і розрахувати правильний шлях руху і дотриматися його, навіть  не маючи під  рукою компаса і карти. 

У туристському поході, під час ігор на місцевості і в деяких інших випадках виникає потреба визначити від­стань до неприступних предметів, виміряти їх довжину, висоту, встановити, скільки ще залишилося шляху до кінця маршруту, яка ширина річки чи іншої перешкоди, яка висота дерева, і якщо його зрубати, то чи ляже воно впоперек глибокого рову замість моста і т. д. А тим ча­сом під руками спеціальних інструментів, рулетки, мір­ної стрічки або метра нема. Як бути, як вийти з цього становища?

Якщо ми знаємо постійні величини якої-небудь дов­жини, кута, хоч би навіть з грубим наближенням, і вміє­мо з їх допомогою зробити найпростіші вимірювання на місцевості, то труднощі можна легко подолати. Юний герой з роману Майна Ріда міг розв'язати свою геоме­тричну задачу в дорозі лише тому, що незадовго до по­дорожі виміряв свій зріст і твердо пам'ятав результати вимірювання.

А постійні і досить точні мірки — похідні еталони або «живі метри», виявляється, завжди ми маємо при собі. От і добре було б кожному мати свій похідний еталон або «живий метр», щоб при потребі користуватися ним для вимірювання.

 

 

 

 

 

 

Похідні еталони

 

Еталон — це стала точна міра. Еталонами можуть бути різні частини людського тіла і дані вимірювань різ­них предметів, що мають стандартні розміри.

Кожному туристові треба насамперед знати свій зріст і висоту від ступні до очей.

Відомо, що між окремими частинами людського тіла є певні співвідношення, які вказують на пропорціональність будови тіла людини незалежно від її абсолютного зросту. Звичайно, майже у кожної людини є деякі відхи­лення від норми. Однак ряд мірних особливостей можна брати до уваги.

Почнемо з лінійних мір.

 

 

                          

 

 

 

Мал. 1                              Мал. 2

 

 

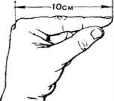
10 см — довжина вказівного пальця у дорослої лю­дини. Для вимірювання його згинають під прямим кутом до  долоні   (мал.   1). Це  дуже  важлива і зручна міра. Якщо палець коротший від 10 см, то цю міру треба запи­сати і запам'ятати.

20 см вкладається між кінцями мізинця і великого пальця, коли розвести пальці і вільно, без напруження покласти руку на планшет чи польову книжку (мал. 2). Ця мірка нагадує циркуль; вона дуже зручна, коли тре­ба швидко відміряти метр та його частини.

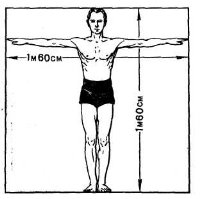
2 м — висота людини з піднятою рукою, яким кисть руки відігнути назад.

1 м — висота від підлоги до поясу людини.

Відстань від кінців пальців однієї руки до кінців пальців другої при положенні «руки в сторони» теж можна використати при вимірюваннях. Слід також па­м'ятати, що в більшості людей відстань між кінцями розведених рук дорівнює зростові (мал. 3).

Численними вимірю­ваннями встановлено цікаве співвідношення: середня довжина кроку дорослої людини дорів­нює приблизно полови­ні її зросту, якщо міря­ти до рівня очей. Якщо, наприклад, зріст люди­ни до

 

 її очей дорівнює 140 см, то довжина її кроку становить близь­ко 70 см. При нагоді пе­ревірте це.

Дуже важливо зна­ти довжину своїх кроків при спокійній ході. Це дасть можливість безпомилко­во рухатись по азимутах і робити правильні знімання пла­нів (схем) місцевості без інструментів.

 

Практикою  встановлено  також,   що довжину свого кроку можна визначити за формулою, де Р — зріст людини в сантиметрах, а 4 і 37 — сталі числа. Напри­клад, при зрості 120 см довжина кроку дорівнюватиме:

см, або заокруглено 0,7 м.

Точніше величину кроку в метрах визначають промі­рюванням кроками лінії, довжина якої відома. Промі­рюють двічі або тричі і остаточним результатом вважа­ють середнє значення замірів.

Багатьом з вас доводилось ходити узбіччям залізни­ці; там зрідка розставлені стовпці з цифровими познач­ками. Відстань між цими стовпцями дорівнює 100 м. Припустимо, що ви з товаришем тричі виміряли крока­ми цю відстань. У вас виходили такі цифри: 143, 145, 147, тобто в середньому 145 кроків. У вашого товариша середнє число кроків між двома стовпцями— 152. Вихо­дить, що ваш крок дорівнює 100 : 145 = 0,69 м, а крок ва­шого товариша — 100 : 152 = 0,66 м.

Узнайте, скільки ваших кроків вкладається в 1 км.

Коли вимірюють відстань на місцевості кроками, від­лік ведуть парами кроків, називаючи порядковий номер під одну яку-небудь ногу, наприклад, під праву; так лег­ше рахувати. Тепер розглянемо, як вимірювати кути без інструментів, за допомогою своїх еталонів.

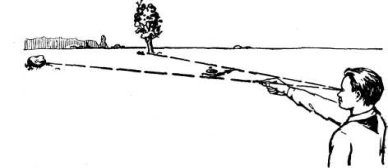
Якщо витягнути праву руку прямо перед собою так, щоб вона не згиналася в лікті і щоб кисть руки була на рівні ока, то відстань від ока до основи вказівного паль­ця дорівнюватиме 57—60 см. Перевірте це в себе. Для тих, хто обізнаний з радіальним вимірюванням кутів, зрозуміло, що на такій відстані кожний сантиметр має кутову величину в 1°.

Оскільки довжина вказівного пальця дорівнює 10 см, то досить зігнути його в основі під прямим кутом до лі­нії всієї руки — і вимірник готовий: між кінцем вказів­ного пальця і його основою, тобто згином, утворюється кут, який дорівнює 10° (мал. 4). Дивитися при цьому треба одним оком, краще — правим, і тримати голову прямо, весь час в одному положенні.

Ця міра кута дуже зручна, бо дає можливість легко знаходити величину будь-якого кута в цілих градусах. Для цього починаємо укладати свою мірку, тобто па­лець, по прямій, що сполучає обидва предмети, між яки­ми вимірюється кут. Сумістивши кінець пальця з одним із предметів, помічаємо, проти чого приходиться другий його кінець; перевіряємо себе кілька разів, і це буде 10°.

Потім переміщуємо палець далі по прямій, суміщуючи його кінець з поміченим місцем, проти якого був перед тим згин пальця; знаходимо нове місце згину; тут кінчаються наступні 10°, тобто це вже 20^е від початку, і т. д. Нарешті, доходимо до другого предмета, який обмежує наш кут. Він, як правило, ляже

 

 

десь посередині пальця, переміщеного далі від попередньої помітки. Тут дове­деться визначити на око, скільки десятих частин пальця буде між його кінцем і візованим предметом — стільки цілих градусів доведеться додати до відміряних перед цим десятків градусів. Наприклад, палець уклали ціл­ком 4 рази і після цього лишилось ще 7/10 його довжи­ни; кут дорівнює 47°.

Коли переставляють палець, не можна порушувати положення руки відносно корпуса тіла і ока; треба слі­дом за пальцем повільно повертатися всім корпусом.

Крім кута в 10°, у нас є дуже зручна міра в 22,5° — від кінця великого пальця до кінця мізинця, якщо трима­ти витягнуту руку прямо на рівні ока і перпендикулярно до променя зору (мал. 5). Цією мірою можна, по-перше,, вимірювати кути в 45^е і 90°, а по-друге, вимірювати ве­ликі кути, бо мірою в 10°, яку довелося б відкладати багато разів, нагромаджується більше похибок.

Міра в 22,5° не така чітка, як міра в 10°. Тому її треба дуже уважно вивчити в себе, звикнути до неї і тоді нею теж легко буде користуватись.

Викладені вище співвідношення між частинами люд­ського тіла — наближені і наводяться як постійні вели­чини для середньої на зріст дорослої людини. У дітей і юнаків навіть одного віку ці величини

 Мал. 5

неоднакові, ос­кільки це зв'язано з ростом та індивідуальними особли­востями. Тому бажано, щоб кожний

 

 

юний турист, готуючись до походу, визначив довжину свого вказівного паль­ця та відстань між кінцями мізинця і великого пальця, як показано на мал. 1 і 2, а також розмір свого кроку. Для вимірювання кутів, а також лінійних величин треба знати такі розміри своєї руки (мал. 6):

1. ширину долоні;
2. ширину долоні без великого пальця;

3. довжину    двох     останніх     суглобів     вказівного пальця;

4. довжину другого суглоба вказівного пальця;
5. ширину великого пальця;
6. ширину мізинця.

Еталонами можуть бути також різні предмети, які мають сталі, стандартні розміри. До них належать: са­перні лопати, туристські сокирки, сірникові коробки, олівці, монети тощо (мал. 7, 8). Ці предмети бувають у туристів, і ними завжди можна скористатися для вимі­рювань, але треба заздалегідь визначити їх розміри і записати. Такі записи слід зберігати при собі, а ще кра­ще — знати їх напам'ять.

 

На око

Тепер ми вже знаємо, що ро­бити, якщо потрібно буде в по­ході визначити розміри майдан­чика для розміщення табору або провести інші вимірювання без рулетки, мірної стрічки, метра: ми скористаємося нашими похід­ними еталонами. А як визначити відстань до неприступного дере­за або встановити, який відрізок шляху ще залишився до міста або до лісу? В такому разі від­стань визначають лише на око.

Здатність людини визначити відстань до навколишніх предме­тів та їх розміри на око, без будь-яких приладів, називається око­міром. Цим способом користу­ються у всякій обстановці і в будь-який час.

На чому ґрунтується здат­ність людини визначати відстань на око? З власного досвіду ви знаєте, що чим ближче до нас предмет, тим ясніше і виразніше ми його бачимо і тим більше роз­різняємо на ньому зовнішніх по­дробиць. Чим ближче розташова­ний предмет, тим він здається більшим, і навпаки, чим далі він,

тим здається меншим. Наприклад, на відстані 2000 м можна розрізнити лише обриси великого дерева, на від­стані 900—1000 м вже видно його стовбур, коли наблизи­тись на 500—600 м, стають помітними великі гілки, на 300—400 м — менші, а на відстані 200 м можна розріз­нити навіть листя.

Кількаразовою перевіркою можна з'ясувати, на якій відстані добре видно гілки на деревах, за скільки метрів можна бачити віконні рами, черепицю на даху, обличчя людини та інші предмети. Такий спосіб визначення відстаней на око називається ступенем видимості місцевих предметів.

Щоб швидко визначити відстань цим способом, тре­ба мати заздалегідь складену для особистого користу­вання табличку, в якій на підставі власного досвіду запи­сати дані видимості місцевих предметів.

Щоб скласти таку табличку, можна в ясний день вийти з групою товаришів у поле і зробити замірювання. Один стає край дороги, а інші йдуть від нього, рахуючи кроки і весь час поглядаючи на товариша, що залишився.

 

Запишіть, на якій відстані ще чітко виділятиметься його обличчя. На більшій відстані вже не можна буде виразно бачити обличчя, але ще видно буде обриси голо­ви і плечей. Запишіть і цю відстань. Дехто бачитиме об­личчя товариша на відстані до 150 м, але більшість роз­різнятиме його лише з відстані 100 м і менше. З відда­ленням обриси голови і плечей зникнуть, видно буде лише невеликий чорний стовпчик, а ще далі — ледве по­мітну точку.

У табличку слід записувати й видимість з різних відстаней місцевих предметів: телеграфних стовпів, різних будівель та ін.

Наводимо таблицю відстаней, складену на підставі досвіду, для людини з середнім зором (Таб. 1). За цим зразком кожний, враховуючи особливості свого зору, може скласти (виробити) таку таблицю, за допомогою якої можна буде більш-менш точно визначати відстань на око за всяких умов.

 

                                                                  Таблиця 1

Складаючи таблицю, слід враховувати ще й такі особ­ливості. На однаковій відстані дрібні предмети (кущі, камені) здаються розміщеними далі, ніж такі великі предмети, як дерева, будівлі, горби. Так само здається, що предмети яскравого кольору знаходяться ближче, ніж предмети сірого, темного кольорів. Якщо яскравий предмет розташований на одноманітній, одноколірній місцевості (рілля, вкрите снігом поле), то цей предмет сприймається так, ніби він розташований ближче, ніж насправді. Строката місцевість, навпаки, віддаляє, маскує предмет. Так само, коли погода похмура, йде дощ. або ліг туман, відстань до місцевих предметів здається більшою, ніж у яскравий сонячний день. На височинах, у гірській місцевості повітря прозоре і тому здається, що предмети розміщені ближче.

Щоб набути доброго окоміру, який може знадобити­ся кожному, особливо туристу, слід призвичаїти око багаторазовими вправами, спостерігаючи не тільки за людьми, а й за будівлями, стовпами, окремими деревами різного забарвлення та розміру, кущами.

Про видимий горизонт

 

Для розвитку окоміру необхідно також мати чітке уявлення про те, як далеко лежить від спостерігача лінія горизонту.   Інакше  кажучи,   потрібно  знати, як далеко можна бачити (коли горизонт відкритий) оточуючу місцевість. Це часто потрібно туристам, мислив­цям і особливо то­пографам і геодези­стам при   рекогнос­цирувальних робо­тах.

Дальність горизон­ту АВ  (мал. 8) лег­ко визначити з прямокутного трикутника АВО, де О — центр Землі, ВО = R (радіус Землі; заокруглено 6400 км), а АО = R + h, де h — висота спостерігача. Дальність го­ризонту АВ — це катет прямокутного трикутника АВО; визначимо його:

Через те, що h завжди дуже мале по відношенню до R, можна вважати, що .

Ця формула буде ще простішою, якщо добути квад­ратний корінь з величини R і коефіцієнта 2:

, або заокруг­лено 113.

Таким чином, формула стане такою:

АВ (дальність горизонту) = 113 км.

Враховуючи, що h (висота спостерігача) знаходиться тут під квадратним коренем, робимо висновок: щоб по­бачити вдвічі далі, треба піднятися приблизно в чотири рази вище.

Наприклад,   стоячи   на   рівнині,  людина, зріст  якої 1,6 м, бачить оточуючу місцевість на 113 = 4,52 км. Піднявшись на дерево, що стоїть окремо, або по рекогносцирувальній драбині на висоту приблизно 6,5 м, людина може бачити навколишню місцевість уже на 113 = 9,04 км.             

Насправді ж дальність видимого горизонту більша, тому що земна атмосфера, викривляючи шлях променів-світла (рефракція), ніби відсуває горизонт приблизно на 6% порівняно з числами, одержаними з формули. Тому людина, що має зріст 1,6 м, бачить оточуючу міс­цевість на 4,8 км, а не на 4,52 км.

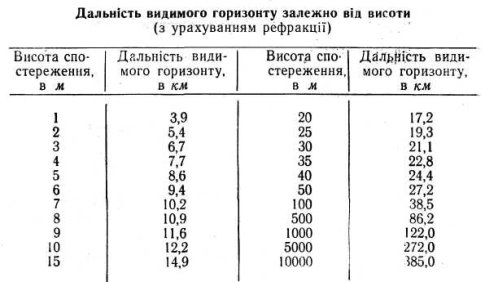
Дальність горизонту збільшується, коли підвищуєть­ся атмосферний тиск, в холодну погоду, а також вранці і ввечері. Як залежить дальність видимого горизонту від висоти, видно з таблиці 2:                      Таблиця 2

 

 

Звичайно, при визначенні відстаней на око треба вра­ховувати те, що зір у людей різний. Тому перш ніж користуватися   цією  таблицею,  треба   перевірити її дані на практиці і зробити для себе поправку.

 

Про далекоміри, які завжди з нами

 

Відстані до предметів визначають за допомогою спе­ціальних приладів та інструментів, які називаються да­лекомірами. Усі далекоміри, особливо фабричного ви­робництва, зроблено так, що їх частини мають сталі кутові або лінійні величини.

У кожної людини теж є сталі величини при собі. Так, у дорослої людини відстань від очей до великого пальця на витягнутій руці дорівнює 60 см, а відстань між зіни­цями очей — 6 см, тобто в 10 раз менша. Це співвідно­шення є величиною майже сталою, як і в далекомірах. У дітей шкільного віку ці розміри менші, але завжди відстань між зіницями очей буде в 10 раз меншою, ніж відстань від очей до великого пальця на витягнутій руці. За допомогою сантиметрової стрічки або довгої лінійки перевірте ці розміри в себе.

Коли користуються далекомірами, треба наперед знати розміри того предмета, до якого визначають від­стань (див. таблицю 3):          Таблиця 3

 

Тепер, коли ви знаєте відстань від ока до великого пальця витягнутої руки і розміри деяких предметів, вва­жайте, що далекомір готовий.

Розглянемо, як користуватися саморобним далеко­міром. Ось ви вийшли на прогулянку або екскурсію за місто і захотілось вам узнати, скільки метрів до фабричного димаря, що підноситься вдалині. Для цього треба простягнути праву руку вперед у напрямі димаря і, виста­вивши догори великий палець, навести його на димар (мал. 10). Дивитися треба лише правим оком на кінець пальця. Тепер, не опускаючи пальця, швидко заплющіть праве і розкрийте ліве око. Палець при цьому ніби від­скочить вбік.

Треба примітити навпроти пальця який-небудь пред­мет. Припустимо, палець закрив дерево, яке знаходить­ся від нас приблизно на такій самій відстані, як і димар. Спробуємо визначити на око, скільки метрів від фабрич­ного димаря до дерева. Не маючи досвіду, зробити це нелегко. Можна порадити умовно відкладати відомі вам відстані в 10, 25 і 50 ж або порівнювати з розмірами предметів. У даному разі вважатимемо, що ця відстань

 

дорівнює 35 м, не більше. Виходить, від нас до фабрич­ного димаря буде в десять раз більше, тобто 350 м. Чому?

Згадаємо геометрію. У вас утворилось два рівнобедрених трикутники: два ока і палець (АСВ) та палець, димар і дерево (ЕСD) — мал. 9. Ці трикутники подібні, тому напишемо таке рівняння:

 

 

Відстань від ока до пальця (60 см) Відстань між очима  (6 см)

Відстань від пальця до димаря (невідома) Відстань між димарем і деревом (35 м)

 

Тепер запишемо це рівняння буквами:

 

Підставимо їх числове значення в метрах:

Ще точніше нашим далекоміром можна визначити відстані за допомогою сірника, міліметрової лінійки. На­приклад, вам потрібно виміряти відстань до телеграф­ного стовпа. Простягнувши руку, наведіть на нього сір­ник (мал. 10). Стовп зайняв на сірнику 12 мм. Як бачимо, знову утворились два подібних трикутники: АОВ і аОв. З цих подібних трикутників можна скласти рів­няння:

 

Мал. 10

 

 

 

АО (відстань від ока спостерігача до телегр. стовпа - невідома) Оа (відстань від ока до сірника - 60 см)

АВ (величина предмета – висота стовпа – 6 м)   аb (виміряна частина сірника - 12 мм)

 

Звідси

Замість сірника можна користуватися звичайною учнівською лінійкою з міліметровими поділками. Якщо у вас не буде під рукою ні сірника, ні лінійки, то можна обійтися власними пальцями. Згадайте про шість розмі­рів своєї руки (мал. 6) — і далекомір готовий.

Ось вам потрібно взнати відстань до пішохода. Про­стягніть руку, підберіть з цих шести положень пальців таке, щоб пішохода цілком закрило. Наприклад, пішо­хода закрило пальцем вашої руки (п'ятий розмір, мал. 6), ширина якого у вас дорівнює 1,5 см. Зріст лю­дини і відстань від ока до великого пальця простягнутої руки відомі. Утворилися знову два подібних трикутники і ті самі два відношення.

Відстань від ока спостерігача до пішохода (невідома) Відстань від ока до великого пальця руки (60 см)

Величина предмета (приблизно зріст пішохода – 1,7 м) Ширина великого пальця руки (1,5 см)

Звідси невідома відстань дорівнює:

(усі величини подано в метрах).

У  деяких   випадках   можна   визначити   відстань   по людині, яка йде вдалині (мал. 11). Для цього заплющіть

ліве око, витягніть руку вперед і відставте великий па­лець. Влучивши момент, коли палець прикриє фігуру людини, що йде, відразу ж заплющіть праве око, а ліве відкрийте. Підрахуйте, скільки кроків зробить людина, поки ваш палець знову прикриє її фігуру. Помножте це число на 10 і одержите кількість кроків до людини. Пе­реведіть кроки в метри.             

Ще   можна  скористатися  таким   далекоміром, який легко зробити самому. Візьміть кусок картону і виріжте в ньому прямокутний трикутник

з основою 80 мм і висо­тою 17 мм. На основу нанесіть поділки через кожний сантиметр і позначте їх цифрами (мал. 12). Далекомір готовий.

За допомогою такого нескладного приладу можна визначити відстань до людини або якогось предмета. Для цього далекомір, тримаючи його за 50 см від очей, пересувайте праворуч або ліворуч так, щоб фігура лю­дини (або предмета), до якої потрібно визначити від­стань, точно вмістилася між сторонами трикутника (мал.   13).  Відлік  на  основі  трикутника проти фігури

людини (предмета) покаже відстань до неї в метрах. На малюнку — 80 м.

Зрозуміло, що всі ці способи вимірювання відстаней (кроками, окоміром або найпростішими далекомірами) неточні. Середня похибка при визначенні відстаней на око становить 10%. У далекомірі з сірника утворюються такі два подібних трикутники, в яких одна сторона в кілька сот раз коротша від двох інших. І по короткій стороні маленького трикутника треба визначати довгу сторону великого. Тут похибка в 1 мм виростає до кіль­кох десятків метрів. Зате окомір і далекомір мають ве­лику перевагу — швидкість.

 

Способи палички і травинки

 

Ви, певно, вже знаєте деякі способи визначення ши­рини річки. Це роблять побудовою подібних прямокут­них трикутників, трикутника з кутами в 45° тощо. Тепер ви дізнаєтесь, як визначити відстань до неприступного предмета або ширину річки без будь-яких побудов на місцевості, використовуючи паличку, олівець або тра­винку. А такі «інструменти» завжди знайдуться.

Розглянемо такий спосіб, який назвемо способом палички. Він, як і бага­то інших способів, ґрунтується на правилах елементар­ної геометрії. Суть його по­лягає  ось у чому.

Станемо на березі річки, простягнемо вперед руку з будь-якою паличкою або олівцем D (мал. 14) так, щоб паличка (олівець) була па­ралельною берегові. Заплю­щивши одно око, будемо ві­зувати на які-небудь предме­ти А і В (кущі, камені то­що), що знаходяться на протилежному березі. Лівий кінець палички суміщаємо з лівим предметом А, а про­ти  предмета В робимо на паличці позначку.

Тепер відійдемо в точку О на деяку відстань Г від берега і по дорозі відміряємо кроками цю відстань. Зно­ву простягнемо перед собою паличку і сумістимо її лі­вий кінець з предметом А. Виявиться, що правий пред­мет В вже не лежить проти зробленої на паличці познач­ки, а відійшов від неї трохи ліворуч.

Зробимо на паличці проти нового положення пред­мета В другу позначку. Таким чином, на паличці, як на малюнку в масштабі, відстань між першою і другою позначкою (D — d) зображає пройдену відстань Г, а відстань d між другою позначкою і лівим кінцем па­лички — шукану ширину річки Ш.

Для підтвердження цього способу звернемося знову до малюнка. Мається на увазі, що спостерігач візує на предмети А і В. Роблячи першу позначку на відстані D від лівого краю, тримає паличку паралельно відстані АВ між предметами.

На підставі подібності трикутників ми можемо на­писати:

де С — відстань між оком і паличкою, L — відстань між предметами А і В.

Так само для трикутника ОАВ можна написати:

 

де d — відстань другої позначки від лівого кінця.

З обох рівнянь виходить, що DШ = L і dН = L, звідки DШ = dН, або .

Замість цього рівняння ми можемо написати рівнян­ня різницеве, тобто:

Тепер запишемо цю формулу так:

 

що й відповідає зазначеному вище правилу, бо D — d становить відстань на паличці між першою і другою по­значками; Г — відстань, пройдена від берега до точки О; d — відстань між другою позначкою і лівим кінцем па­лички, їх відношення дорівнює відношенню пройденого шляху Г до шуканої відстані Ш. Тому

Наприклад, якщо ми відійшли від берега на 100 кро­ків і побачили, що відрізок D — d вкладається у відріз­ку d, скажімо 3,1 раза (це відношення легко знайти, якщо користуватися лінійкою з міліметровими поділка­ми), то треба 100 кроків помножити на 3,1 і дістанемо шукану ширину річки:

Ш= 100x3,1 =310 кроків.

Знаючи розмір свого кроку, неважко перевести цю ширину на метри. Цей спосіб зручний тим, що дає мож­ливість виконувати роботу, не пересуваючись уздовж берега, і при певній навичці забезпечує точні результати.

А ось спосіб травинки.

 

Вам треба швидко визначити ширину річки, а під ру­ками нема ні олівця, ні палички. Зірвіть травинку. На протилежному березі виберіть два помітних предмети. Станьте до них обличчям з простягнутими руками, в яких затиснута травинка, паралельна до уявної лінії між цими предметами. Закрийте проміжок між вибра­ними предметами. При цьому одне око треба заплющити. Тепер складіть травинку пополам і відходьте від бе­рега річки доти, поки відстань між вибраними предме­тами не закриється складеною травинкою. Примітьте місце зупинки і виміряйте кроками відстань між двома  точками вашого стояння. Переведіть кроки на метри. Це й  буде  відстань,  яка дорівнює ширині річки (мал. 15).

Спосіб козирка

 

Ось яким способом скористався сержант Денисов у фронтовій обстановці, щоб виміряти ширину річки. Наші частини переслідували противника. На їх шляху — вод­на перепона. За одержаними відомостями, всі мости че­рез неї зірвано. Де вибрати найзручніше місце для пере­прави? Яка ширина річки? Чи є броди? Щоб знати все це, потрібно зробити розвідку. Виконати це завдання ко­мандир наказав відділенню сержанта Денисова.

Розвідники швидко добралися до річки. Насамперед

 

вирішили виміряти її ширину. Але як? Сержант Денисов став на березі обличчям до річки і насунув кашкета так, щоб з-під козирка було видно тільки лінію протилежно­го берега — уріз води — і намітив там точку — В (мал. 16, а). Не змінюючи положення кашкета, він по­вернувся ліворуч і намітив на своєму березі точку С, яка виднілася з-під козирка (мал. 16, б). Тепер, щоб визна­чити ширину річки, треба було тільки виміряти відстань до точки С. Вона становила 150 м.

Пояснюється цей спосіб так. Промінь зору, що тор­кається обрізу козирка, спочатку направлений на уріз води   протилежного   берега — в   точку В. Коли людина

повертається, то промінь зору, як ніжка циркуля, ніби описує коло, і тоді АС=АВ як радіуси одного кола.

Вимірювати таким способом віддалі до предметів можна й за допомогою долоні, записної книжки тощо, приклавши їх над очима під певним кутом. Тільки треба пильно стежити за тим, щоб не змінити величини цього кута.

 

Визначення відстаней по звуку і світлу

 

Швидкість звуку в повітрі — близько 300 м за 1 сек або приблизно 1 км за 3 сек. Світло звичайно поши­рюється миттєво. Цю властивість світла й звуку можна використати при орієнтуванні на місцевості. Так, від­рахувавши, скільки секунд минуло від спалаху блискав­ки, пострілу, гудка теплохода чи тепловоза, удару моло­том і т. п., можна досить точно визначити відстань до джерела звуку. Припустимо, вдалині спалахнула блис­кавка, а гуркіт грому почувся лише через 10 сек. Отже, відстань до грозової хмари не менша, як 3 км.

Якщо нема годинника, неважко відрахувати секунди мовчки: о-дин, д-ва, т-ри. За цей проміжок часу (одиничний відлік трьох секунд) звук і пройде відстань, що до­рівнює 1 км.

Звуки чути приблизно на такій відстані:                Таблиця 4

 

Як визначити висоту дерева

 

Висоту дерева або будь-якого іншого предмета мож­на визначити кількома способами.

По тіні. Якщо на рівному місці кроками виміряти одночасно довжину своєї тіні і тіні, яку відкидає дерево (чи якийсь інший предмет), то шукану висоту останнього легко можна обчислити з рівняння (мал. 17):

де АС — висота дерева (Н), ас — ваш зріст (h), СВ— тінь від дерева (D), сb — ваша тінь (d).

На підставі цього відношення, виведеного з подіб­ності трикутника АВС і аbс, можна зробити висновок, що висота дерева (предмета) в стільки разів більша від ва­шого зросту, в скільки разів тінь, яку відкидає дерево (предмет), довша від вашої тіні.

Наприклад, довжина вашої тіні d=3 крокам, а тінь дерева D = 9 крокам, тобто тінь дерева втричі довша, ніж ваша. Якщо прийняти ваш зріст за 1,5 м, то висота дере­ва буде: Н= 1,5·3=4,5 м.

По жердині. Цим способом можна скористатися при похмурій погоді, коли предмети не дають тіні. В цьо­му випадку для вимірювання слід взяти

жердину такої довжини, як зріст спостерігача (мал. 18), і встановити її на такій відстані від де­рева, щоб лежачи можна було бачити верхівку дерева на одній прямій лі­нії з верхівкою жердини. Висота дерева дорівнюва­тиме відстані від голови спостерігача до основи дерева, як це видно на малюнку, тобто АС = ВС.
По калюжі або дзеркалу. Цей спо­сіб можна застосувати після дощу, коли на зем­лі багато калюж. Вимі­рювання роблять так. Знаходять поблизу дерева, висоту якого треба визначити, ка­люжу і стають біля неї так, щоб вона була між деревом і спостерігачем (мал. 19). Потім знаходять точку, з якої

 

видно відображену у воді верхівку дерева. Це дерево буде в стільки разів вищим від зросту спостерігача, у скільки разів відстань від нього до калюжі (ВО) біль­ша відстані від калюжі до спостерігача (АО).

Замість калюжі можна скори­статися дзеркальцем, положивши його на землі го­ризонтально так, щоб було видно верхівку дерева. По трикутнику. Для цього треба мати прямо­кутний трикутник, обидва гострі кути якого мають по 45°. Користують­ся ним так. Відхо­дять від дерева на деяку відстань і прикладають трикутник до ока так, щоб один з його катетів був пара­лельним вертикальній осі дерева, другий — паралельний земній поверхні, а гіпотенуза була лінією візування. Змі­нюючи поступово точку стояння, добиваються такого по­ложення, щоб лінія візування пройшла через верхівку дерева

В (мал. 20).

Тоді матимемо два подібних трикут­ники АВС і Аbс. У трикутнику Аbс bс=Ас, тому і в три­кутнику АВС ВС=АС, де АС = а — відстань від спосте­рігача до дерева.

Висоту дерева визначають за формулою D = а + К, де К — зріст спостерігача, D — висота дерева, Отже, висота дерева дорівнює відстані від спостерігача до де­рева плюс зріст спостерігача.

Цим способом часто користуються топографи і геоде­зисти при польовому дешифруванні аерофотознімків, для визначення середньої висоти лісу з точністю до 1 м.

 

 

                                      ЛІТЕРАТУРА

1.Курилова В.И.Туризм –М.: Просвещение, 1988

2. Рощин О.М. Без компаса і карти. – Київ: Радянська школа, 1971

3. Рощин А.Н. Ориентирование на местности. – Київ: «Вища школа», 1982