Розробка уроку алгебри і початків аналізу в 11 класі на тему: «Підсумковий урок з теми «Показникова функція». Урок-засідання показникових акціонерних товариств»

Розробка уроку алгебри і початків аналізу в 11 класі на тему: «Підсумковий урок з теми «Показникова функція». Урок-засідання показникових акціонерних товариств»

Тема:Підсумковий урок з теми «Показникова функція». Урок-засідання показникових акціонерних товариств.

Мета:освітня: узагальнити вивчений матеріал з теми «Показникова функція»; закріпити навички розв’язування показниковихрівнянь та нерівностей;

розвиваюча: розвивати вміння виділяти головне, істотне,культуру математичного мовлення;

виховна: виховувати культуру спілкування, пізнавальний інтерес до математики,комунікативні здібності учнів, формування економічної свідомості та раціонального використання людських ресурсів.

Тип уроку: узагальнення та систематизація знань, умінь, навичок.

Обладнання: таблиця «Показникова функція та її графік», комп’ютер, проектор, роздатковий матеріал.

Хід уроку

1.                     Організаційний етап. Підготовка учнів до уроку.
2.                  Перевірка домашнього завдання. Перевірити наявність домашнього завдання. Дати відповідь на питання учнів, що виникли під час виконання домашньої роботи.
3.             Мотивація навчальної діяльності.

Сьогодні у нас не просто урок, а урок – засіданняпоказникових акціонерних товариств (ПАТ) «Властивість», «Рівняння», «Нерівність». Представляються президент і віце – президент, секретар,директор фінвідділів кожного ПАТ.

На уроці кожне ПАТ виступає за такою програмою:

1.                   Доповідь президента.
2.                   Промислові відношення – узагальнення проводить віце-президент.
3.                   Упровадження пропозиції у практику - розв’язаннявправ з пакету документів «Державна підсумкова атестація» виконує секретар.
4.                   Розпродаж акцій і контроль економічних справ показникового ринку (розв’язування карток і оцінювання за шкалою 12 балів) проводить директор фінвідділу.

4.              Актуалізація опорних знань.

1.                   1) Слово надається президенту ПАТ «Властивість»

Учень дає означення показникової функції, використовуючи таблицю «Показникова функція та її графік», розповідає історію вивчення показникової функції.

Функція, яку задано формулою y=a^x, де a>0, a≠1 називається показниковою, а – основапоказникової функції. Якщо а=1, то функція y=a^x=1^x=1 є сталою.

Графіком показникової функції є експонента, яка розташована у I та II координатних  чвертях, тому що вирази (-2)^3/4; 0^-1; 0⁰; 0^-1/8 позбавлені смислу.

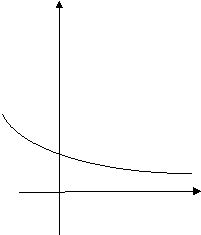
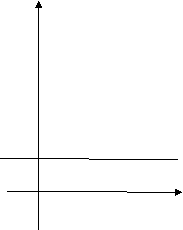      а                                         0                              а = 1

у                                                        уу

 

 

 

         1                                                 1                                           1    

0                                           х           0                                        х         0                                      х

 

Графік функції у=а^х і у=()^x симетричні відносно осі ординат.

Питання, пов’язане з показниковою функцією, розробляв Леонард Ейлер (15.04.1707-18.09.1783). Він народився у швейцарському Базелі в сім’ї небагатого пастора Пауля Ейлера. Його мати Маргарита походила з освіченої родини. Батько був математично обдарованою людиною й навіть написав дисертацію про співвідношення і пропорції. Він і став першим учителем свого сина. Незвичайна обдарованість хлопчика виявилася досить рано. У віці 13 років Леонард вступив до Базельського університету, де слухав лекції з математики Йоганна Бернуллі. А через чотири роки Ейлер – молодиймагістр філософії – прочитав латиною свою першу лекцію про порівняльну характеристику філософії Декарта і Ньютона.

Життя вченого нараховує 60 років творчої діяльності. Ейлер написав близько 760 статей для часописів, 40 книжок, а 15 його праць було підготовлено до різноманітних конкурсів.

У двох розділах своєї праці «Вступ до аналізу» він описав «показникові й логарифмічні кількості». До перших належать а^х, до других у^х. Навіть і сам показник може бути показниковою «кількістю», наприклад у виразах .

Ейлеру належить відкриття зв’язку між показниковою і тригонометричними функціями.

Показникову функцію виду у=е^х почали вивчати з 40 років XVII століття.

Іранський математик ал – Караджі почав розглядати тричленні рівняння, квадратні відносно деякого степеня невідомого, а також рівняння, що зводяться до них діленням на степінь невідомого, тобто рівняння виду

ax²ⁿ+bxⁿ=c,    ax²ⁿ+c=bxⁿ,   bxⁿ+c=ax²ⁿ,   ax^2n+m=bx^n+m+cxⁿ

2) До слова запрошується віце-президент. Він називає основні властивості показникової функції, розповідає про її застосування в інших галузях науки.

Властивості показникової функції

• Область визначення: всі дійсні числа.
• Область значень: усі додатні числа.
• Нулі: немає.
• Проміжки знакосталості: y>0 у всій області визначення; y<0 не існує.
• Монотонність: якщо а>1, функція зростає; якщо 0<a<1, функція спадає у всій області визначення.
• Парність, непарність:  функція загального виду (функція ані парна, ані непарна).
• Точка перетину з віссю у: (0;1). З віссю х не перетинається.
• Періодичність: неперіодична.
• Екстремуми:  немає.
• Графіком є експонента.

«Експонента»

Як запам’ятати наближене значення числа е ( експонента) ?

Вперше позначення цієї константи літерою е ввів Леонард Ейлер у 1727 році. Чому він позначив цю константу саме літерою е достеменно невідомо.

Можливо це пов’язане з тим, що з неї починається слово exponenta (показниковий, експоненціальний). А може, тому що літери a,b,c,d  уже були «зайняті» і e виявилося першою вільною?

                                  e=2,718281828459045…

Як запам’ятати перші цифри цього числа?

Можна запропонувати  таке правило: 2,7, далі двічі рік народження Льва Толстого (1828), потім величини кутів прямокутного рівнобедреного трикутника (45, 90, 45), або рік перемоги над фашистами, подвоєний рік і знову він.

Є віршик, який дозволяє запам’ятати перші 12 знаків цього числа після коми (кількість літер у словах – цифри константи).

Мы порхали и блистали, но застряли в перевале,

Не признали наши крали авторалли.

Цифри числа eлегко пов’язати з президентом Америки Ендрю Джексоном: 2 – стількиразів його обирали президентом, 7 – бувсьомим президентом Америки, 1828 – рікйого обрання.

Література: Шаніна Л.М. Півхвилинки відпочинку на уроці / Л.М. Шаніна //Математика в школах України. – 2012. – №6. – С. 12-15.

Багато процесів у природі і техніці математично виражаються за допомогою показникової функції, тобто показникова функція є математичною моделлю цілої низки процесів, які відбуваються в природі та в діяльності людини.

Фізика. Задача про радіоактивний розпад розв’язується за формулою N₀/N=2^x/T, де N₀-початкова кількість радіоактивної величини, Т-період напіврозпаду радіоактивної величини, х-час.

Метеорологія. Задача про зміну атмосферного тиску. Атмосферний тиск змінюється залежно від висоти h над рівнем моря за законом p =p₀a^h,де p₀- атмосферний тиск на рівні моря, а – стала.

Біологія. Задача про розмноження бактерій. Розмноження бактерій відбувається за законом N=N₀a^kt_, де N₀-початкова кількість бактерій при t=0, a i k – деякісталі.

Задача про приріст деревини. Кількість деревини з часом збільшується за законом M=M₀a^kt, де М - кількість деревини у даний момент, м³; М₀ – початкова кількість деревини, t-час (у роках), k - стала.

Банківська справа. Якщо покласти гроші у банк під певний процент, то кожного року кількість грошей на рахунку буде збільшуватися в одну й ту саму кількість разів. Тому показникова функція описує цей процес.

Техніка. Задача про вакуумування. Під час вакуумування кінцевий тиск пов’язаний з початковим тиском співвідношенням

P₂=()^nt/3 p₁, де

Р₂ – кінцевийтиск, мм рт. ст.; р₁– початковийтиск, мм рт. ст..; R - об’єм, що підлягає відкачуванню, см³; Q - об’єм газу, що відкачується насосом за один оберт, см³; n- кількість обертів насоса, об./хв; t - час вакуумування, хв.

3) Під час виступу президента і віце-президента секретар на дошці розв’язує вправу з підручника Є.П.Неліна «Алгебра і початки аналізу. 10 клас».

Завдання. Порівняйте значення виразів:

а) ()^1,3 та ()^1,8;                б) (5,3)^-8 та (5,3)⁴.

Розв’язання. Застосуємо властивості показникової функції.

а) 0 < а = < 1, тому показникова функція спадає; 1,3<1,8, отже ()^1,3>()^1,8.

б) а = 5,3 > 1, тому показникова функція зростає; -8<4, отже (5,3)^-8<(5,3)⁴.

2. 1) Слово надається команді ПАТ «Рівняння». Президент дає означення показникового рівняння, вводить поняття найпростішого показникового рівняння, розповідає про спосіб його розв’язання. Наводить приклади.

Показниковим називають рівняння, в яких невідоме входить лише до показників степеня при сталих основах.

Найпростішим показниковим рівнянням є а^х=в, де а>0, a≠1,b>0. Якщо замість х у показнику степеня стоїть деяка функція f(x), то a^f(x)=b, a>0, a≠1, b>0.

Наприклад: 5^х=125;        3^х-2=;           2^-x=16.

Загального методу розв’язування показникових рівнянь немає. Можна виділити кілька типів показникових рівнянь і навести схеми їх розв’язування.

2) Віце-президент називає основні методи розв’язання показникових рівнянь та нагадує учням властивості степеня.

Способи розв’язування показникових рівнянь:

• зведення до однієї основи;
• введення заміни;
• зведення до однакового показника;
• винесення спільного множника за дужки;
• графічний;
• зведення до двох основ та розв’язування однорідного рівняння.

Властивості степеня

aⁿ×a^m=a^n+m,                        a¹=a,

aⁿ:a^m=a^n-m,                           (aⁿ)^m=a^nm,

aⁿ/bⁿ=(a/b)ⁿ, b≠0,                aⁿbⁿ=(ab)ⁿ,

                   a⁰=1, a≠0,                              a^-n=, a≠0.

3) Виробничий відділ представляє завдання. Учні обговорюють план розв’язку кожного рівняння, далі працюють самостійно з наступною перевіркою за готовим розв’язанням, яке було записане на дошці заздалегідь,

a);                         б)49^х-6×7^х-7=0,                              в)5^х+5^х+2=130,

,                                7^х=t>0,                                      5^х+5^х×5²=130,

  х²-4х=- 3,                                    t²-6t-7=0,                                    5^x(1+25)=130,

  x²-4x+3=0,                                   t₁+t₂=6,  t₁×t₂=-7,                        5^x=

  x₁==3,                               t₁=7, t₂=-1<0,                                     5^x=5,

   x₂==1.                                     7^x=7,                                               х=1.

                                                           x=1.

Відповідь:{1;3}                           Відповідь:{1}                           Відповідь:{1}

1.                   Слово надається президенту ПАТ «Нерівність».

1) Президент дає означення показникової нерівності: показниковими нерівностями називаються нерівності виду a^x>b, a^x≥b, a^f(x)≤b. Розв’язок таких нерівностей базується на застосуванні властивостей показникової функції:

1.                    якщо а>1, то функція а^х зростає, тобто більшому значенню функції відповідає більше значення аргументу, тому а^х>a^c => x>c;
2.                   якщо основа 0<a<1, то функція спадає, тобто більшому значенню функції відповідає менше значення аргументу, тому а^х>a^c=> x<c.

2). Секретар ПАТ «Нерівність» пропонує завдання:

1.                    3^2-x>27,                                  б),,

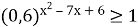3^2-x>3³,                                       ,

a=3>1, тому                              а=0,6<1, тому

2-x>3,                                         x²-7x+6≤0,

-x>3-2,                                        x₁=6, x₂=1,

-x>1,                                           (x-6)(x-1)≤0,

  x<-1.                                               +                                      + 

 

Відповідь: хє( - ∞ ;1)          Відповідь:хє[1;6]

Підсумок цього етапу уроку проводить секретар-референт.

Ми провели засідання показникових акціонерних товариств, на якому повторили пройдений матеріал з теми «Показникова функція», закріпили навички розв’язування рівнянь та нерівностей.

5.                  Вдосконалення вмінь та навичок.

Секретар-референт. А зараз у свої права вступають директори фінвідділів ПАТ і проводять благодійний розпродаж акцій. Це завдання з теми. Акціонери розв’яжуть їх та проведуть обмін акціями (кожен акціонер працює над двома акціями).

Пакет акцій

1.                   Розв’яжіть рівняння:

1.     4^х=8;                                         4)7^cosx=49;
2.     3^х=-9;                                         5)5^2х-6×5^х+5=0;
3.     2^х+2+2^х=40;                                6).

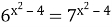2.                   Розв’яжіть нерівність:

1)2^x>1;                                      4)(0,3)^x≤0,49;

2)3^x≥;                                         5);

3)4^5-2x<0,25;                                 6).

Учні здають зошити на перевірку.

6.              Підсумок уроку.

Сьогодні ми систематизували матеріал, що стосується розв’язування показникових рівнянь і нерівностей. Результатом нашої роботи може бути  «юридична шпаргалка» – коротканаочна таблиця-схема.

Міні-підручник

Тема.Показникова функція.

Розв’язування показникових рівнянь і нерівностей

 

Властивості показникової функції y=ax, a>0,a≠1 a>1                                                 0<a<1                                                a=1    у                                                    уу           1                                                  1                                                1                                                                        0                                     х             0                               х             0                                  х   1.D(ax)=R.       2.E(ax)=(0;+).       3.Зростає при а>0.    4.Спадає при 0<а<1.

 

 

Розв’язування показникових рівнянь

Способи розв’язання

1.Зведення рівняння до однієї основи 25х=42х+1, 25х=24х+2, 5х=4х+2, х=2. Відповідь:х=2

2.Зведення рівняння до алгебраїчного(введення нової змінної) 32х-10x3х+9=0, 3х=t>0, t2-10t+9=0, t1=9, t2=1 3x=9 або 3х=1, х=2   або  х=0. Відповідь:{0;2}

3.Винесення спільного множника за дужки 3x5х+3+2x5х+1=77, 3x5хx125+2x5хx5=77, 5х(375+10)=77, 5хx385=77, 5х=, 5х=5-1, х=-1. Відповідь:х=-1.

 

Розв’зуванняпоказникових нерівностей

Схема рівносильних перетворень найпростіших показникових нерівностей

а>1 аf(x)>ag(x)f(x)>g(x), знак нерівності зберігається, 2х-1>4, 2х-1>22, а=2>1, функція y=2x зростає, тому х-1>2,  x>3. Відповідь:хє(3;+

0<a<1 af(x)>ag(x) знак нерівності змінюється на протилежний (0,5)х-3 (0,5)х-3 а=0,5 спадає, тому х-3 Відповідь:хє[5;+

Підбивається підсумок виступу кожного ПАТ, аналізується активність учасників, помилки.

7.          Домашнє завдання.

1.                   Підготуватися до контрольної роботи.
2.                   Розв’язати тест №2, завдання 1-5, 17(а,б)

(Мерзляк А. Алгебра. 11 клас / А. Мерзляк А., Д. Номировський, В. Полонський, М. Якір. – Х. : Гімназія,2011. – 235 с.)