Розробка уроку геометрії на тему « Куля і сфера.»
Мета уроку: сформуватипоняття:
·Кулі;
·Сфери;
·Центра кулі ( сфери);
·Радіуса кулі ( сфери);
·Хорди кулі ( сфери);
·Діаметра кулі ( сфери);
·Діаметрально протилежно протилежних точок.
Домогтися засвоєння:
üВипадків взаємного розміщення кулі й площини в просторі;
üТеореми про переріз кулі.
Сформувати вміння знаходити елементи кулі ( сфери); визначати взаємне розміщення площини і кулі ( сфери) в просторі; застосовувати теорему про переріз кулі до розв'язування задач.
oРозвивати просторове уявлення, логічне мислення, пам'ять, увагу;
Виховувати наполегливість, працьовитість, акуратність
Розробка уроку геометрії на тему « Куля і сфера.» Викладач Токар С. М.
Мета уроку:
- Кулі;
- Сфери;
- Центра кулі ( сфери);
- Радіуса кулі ( сфери);
- Хорди кулі ( сфери);
- Діаметра кулі ( сфери);
- Діаметрально протилежно протилежних точок.
Домогтися засвоєння:
- Випадків взаємного розміщення кулі й площини в просторі;
- Теореми про переріз кулі.
Сформувати вміння знаходити елементи кулі ( сфери); визначати взаємне розміщення площини і кулі ( сфери) в просторі; застосовувати теорему про переріз кулі до розв’язування задач.
- Розвивати просторове уявлення, логічне мислення, пам’ять, увагу;
- Виховувати наполегливість, працьовитість, акуратність, повагу до обраної професії.
Обладнання уроку: моделі кулі і сфери, презентація «Куля і сфера», повітряні кульки, апельсин, аркуш картону, круг з віссю – дротиком, кронциркуль, штангенциркуль, основи для колажу, 2 конверти.
Тип уроку: комбінований.
Хід уроку.
- Організаційний етап.
- Перевірка домашнього завдання. Актуалізація опорних знань.
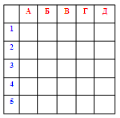
- Встановити відповідні пари:. Встановити відповідні пари:
|
1. Довжина кола … 2. Діаметр кола… 3. Площа круга … 4. Довжина півкола … 5. Подвоєна площа круга …
|
А) 2R Б) 2πR B) πR2 Г) 2πR2 Д) Інша відповідь
|
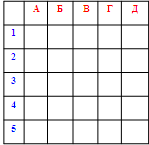
В прямокутному трикутнику…
|
1. Відношення прилеглого катета до гіпотенузи … 2. Відношення протилежного катета до гіпотенузи … 3. Відношення протилежного катета до прилеглого … 4. Відношення прилеглого катета до протилежного … 5. Відношення сторони трикутника до синуса протилеглого кута
|
А) 2R Б)sinα B)cosα Г) tg α Д) ctgα
|
|
- Повідомлення теми, мети й завдань уроку.
Слово викладача.
Дитячий м’ячик, тенісний або футбольний м’яч, повітряна кулька… У кожного з вас свої спогади. При вивченні, наприклад, географії або астрономії прямо пов‘язані з таким тілом, як куля. Географічні паралелі –це лінії перетину поверхні Землі ( яку ми ідеалізуємо, вважаючи кулею) площинами, паралельними площині екватора. Сьогодні ви з’ясуєте поняття кулі та її поверхні ,дізнаєтеся про взаємне розташування в просторі кулі і площини і навчитесь розв’язувати основні типи задач про кулю і сферу.
Приклади матеріальних куль:
кульки підшипника, спортивні ядра, цукерки – драже тощо. Форму, наближену до кулі, мають Земля, Місяць, Сонце, інші небесні тіла.
- Сприйняття і усвідомлення нового матеріалу.
(проводиться у формі конференції).
План вивчення теми.
- Означення кулі (сфери) ,її центра і радіуса.
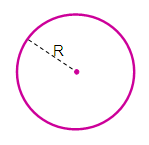
Кулею називають множину всіх точок простору, віддалених від даної точки на відстань, що не перевищує задану. Цю точку називають центром кулі, а задану відстань – радіусом кулі.
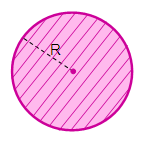
Кулею називають тіло, утворене обертанням круга навколо його діаметра.
Поверхню кулі називають сферою.
Або сферою називають тіло, утворене обертанням кола навколо його діаметра.
- Означення хорди, діаметра, діаметрально протилежних точок кулі ( сфери).
Відрізок, що сполучає дві точки сфери, називають хордою сфери ( кулі).
Хорду, яка проходить через центр сфери, називають діаметром сфери ( кулі).
Кінці діаметра називають діаметрально протилежними точками.
Діаметр дорівнює двом радіусам кулі:
d =2 r
- Взаємне розміщення кулі і площини у просторі.
Як можуть розміщуватися в просторі куля і площина ?
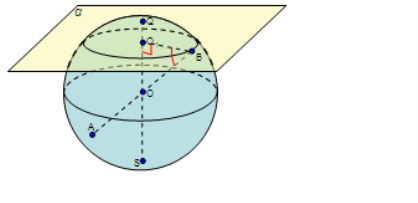
Можливі 3 випадки (d- відстань від центра кулі до площини, r- радіус кулі)-мал. 193:
- Площина і куля не мають спільних точок (r<d) - мал. а;
- Площина і куля мають безліч спільних точок (r>d) - мал. б;
- Площина і куля мають одну спільну точку (площина називається дотичною до кулі). Спільна точка площини і кулі називають точкою дотику. (r =d) - мал. в;
- Теорема про переріз кулі.
Дослідження. Переріз кулі площиною.
(розглянемо на прикладі апельсина і аркуша картону).
- Уявлення про яке тіло нам дає апельсин? А аркуш картону?
- Відтинаємо сегмент - це частина кулі.
Площина перетинає кулю по кругу.
- Уявлення про яке тіло нам дає шкірка апельсина?
- Давайте подивимось, по якій фігурі перетнула площина шкірку апельсина (по кругу чи по колу)?
Площина перетинає сферу по колу.
Теорема. Будь – який переріз кулі площиною є круг. Центр цього круга – основа перпендикуляра, опущеного з центра кулі на січну площину.
Наслідок. Будь – який переріз сфери площиною є коло. Центр цього кола є основою перпендикуляра, опущеного з центра сфери на січну площину.
- Означення діаметральної площини.
Діаметральна площина – це площина, яка проходить через центр кулі . Переріз кулі діаметральною площиною - це великий круг, а переріз сфери – велике коло.
( продемонструвати на апельсині.)
- Формула для обчислення площі сфери.
Площу сфери обчислюють за формулою :
S=4πR2 .
Площі двох сфер відносяться як квадрати їх радіусів або діаметрів.
- Осмислення нового матеріалу. Формування вмінь та навичок.
Колективне розв’язування задач під керівництвом вчителя.
(Усно):
- Чи можна з дерев’яної кулі радіуса 6 см виготовити циліндр заввишки 1 см, діаметр основи якого дорівнює 12 см ? Відповідь пояснити.
1. Геометрична фігура, що складається з усіх точок площини, рівновіддалених від однієї точки цієї площини 2. Геометричне тіло, що утворюється від обертання круга навколо діаметра… 3. Тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану … 4. Геометрична фігура, яка утворюється від обертання кола навколо діаметра ... 5. Поверхня, яка складається із всіх точок простору, що знаходяться на даній відстані від даної точки …
|
А) Куля Б) Коло В) Сфера Г) Круг Д) Інша відповідь
|
Відповідності: А -……..
Б -………
В - ……..
(Письмово):
- Площина перетинає кулю. Площа перерізу дорівнює 4π см2. Знайти радіус кулі, якщо кут нахилу цього радіусу до площини перерізу дорівнює 60˚.
- Кулю радіуса 15 см перетинає площина, віддалена від її центра на 9 см. Знайдіть площу перерізу.
- Для фарбування кулі діаметром 2 дм потрібно 30 г фарби. Скільки фарби потрібно для фарбування кулі діаметром 6 дм?
- Приміщення виставки має вигляд півкулі, площа сферичної поверхні якої – 392π м2 . Визначте діаметр підлоги.
- Задачі з несподіваною відповіддю (проводиться у формі дискусії).
- (Демонструється «повітряна кулька»). Чи можна «повітряну кулю» називати кулею ?
- Мильний міхур – це куля чи сфера?
- (Демонструється дерев’яна куля, пластикова сфера).
- Як знайти радіуси цих тіл обертання? Як виміряти діаметри цих предметів?
Діаметри невеликих матеріальних куль вимірюють кронциркулем ( мал.197) або штангенциркулем (мал..198)
- Підбиття підсумків уроку.
З групи формуються 3 команди.
- Створення колажу. (Кожна з 2 команд по 7 учнів отримує конверт із завданнями для формування колажу. Після виконання кожного завдання 1 учень підходить до основи колажу, кріпить відповідь. І так далі.)
Колаж «Куля»
- Чи можна з дерев’яного циліндра,
діаметр основи якого дорівнює 11 см,
а висота 8 см,
виготовити кулю радіуса 5 см?
Так. Ні. (підкреслити).
- Радіус кулі дорівнює 4 см.
Площа великого круга………….см2
- Переріз кулі
площиною -
це ………………
- Найбільша хорда
кулі називається
……………………
- Куля утворюється
обертанням ………….
навколо його
……………………
________________________________________________
Колаж «Сфера»
- Яка фігура утворюється
при перетині двох сфер?
…………………….
- Довжина великого кола
дорівнює 12π см.
Радіус сфери = ………см.
- Сфера – це
…………………….. кулі.
- Переріз сфери
площиною – це ……..
- Кінці діаметра називають
………………………………….
точками.
- Гра «Вірю – не вірю» (решта учнів).
Чи правильно, що:
А) усі точки кулі віддалені від її центра на відстань, що дорівнює радіусу кулі;
Б) центр сфери не належить поданій сфері;
В) відстань між будь – якими точками кулі не більша від діаметра кулі;
Г) будь – який переріз сфери площиною є колом;
Д) з – поміж двох перерізів кулі площинами більшим є той, який розташований ближче до центра;
Е) будь – який переріз кулі площиною є колом;
Є) відстань між будь – якими точками сфери не більша від діаметра сфери;
Ж) радіус будь – якого перерізу сфери площиною менший від радіуса сфери.
Скласти ключ – відповідь. ( ___ - ні ; ![]()
---![]()
![]()
![]()
- Рефлексія. Твій настрій:
ДОДАТКИ.
Задача 1
Площина перетинає кулю. Площа перерізу дорівнює 4π см2. Знайти радіус кулі, якщо кут нахилу цього радіусу до площини перерізу дорівнює 60˚.
Розв’язання.
Sкр. = πr2 – площа перерізу кулі площиною.
πr2 =…
r2 =…
r =… , О1В =r =…
З Δ ОО1В (<О1= 90˚):
…60˚= ![]() , ОВ =…см - радіус кулі.
, ОВ =…см - радіус кулі.
Відповідь: радіус кулі … см.
Задача 2
Кулю радіуса 15 см перетинає площина, віддалена від її центра на 9 см. Знайдіть площу перерізу.
![]()
![]()

![]()
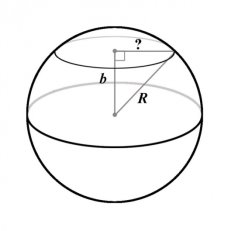
Розв’язання.
Sкр. = πr2 – площа перерізу кулі площиною.
R=… см, H=… см
За теоремою про………………………………………….
З Δ ОО1В (<О1= 90˚):
r2 = R2 – H2
r2 =…..-…..
Тоді Sкр. = πr2 = ……(см2)
Варіант відповіді:______
Задача 3
Для фарбування кулі діаметром 2 дм потрібно 30 г фарби. Скільки фарби потрібно для фарбування кулі діаметром 6 дм?
Розв’язання.
Площу сфери обчислюють за формулою :
S=πd2.
d1=2 дм, S1=……..(дм2)
d2=6 дм, S2=……..(дм2)
Складаємо пропорцію: …………..дм2--------- 30г
…………..дм2--------- х г
Отримуємо: ![]()
Х=………..(г)- фарби.
Відповідь:…….. г фарби.
Задача 4
Приміщення виставки має вигляд півкулі, площа сферичної поверхні якої – 392 π м2 . Визначте діаметр підлоги.
Розв’язання.
Площу сфери обчислюють за формулою :
S=πd2.
Діаметр підлоги – це площа великого…………..
S=πd2=…………. м2
d2=………….
d=…………м
Відповідь: ……..м
План вивчення теми.
- Означення кулі (сфери) ,її центра і радіуса.
Кулею називають множину всіх точок простору, віддалених від даної точки на відстань, що не перевищує задану. Цю точку називають центром кулі, а задану відстань – радіусом кулі.
Кулею називають тіло, утворене обертанням круга навколо його діаметра.
Поверхню кулі називають сферою.
Або сферою називають тіло, утворене обертанням кола навколо його діаметра.
- Означення хорди, діаметра, діаметрально протилежних точок кулі ( сфери).
Відрізок, що сполучає дві точки сфери, називають хордою сфери ( кулі).
Хорду, яка проходить через центр сфери, називають діаметром сфери ( кулі).
Кінці діаметра називають діаметрально протилежними точками.
Діаметр дорівнює двом радіусам кулі:
d =2 r
- Взаємне розміщення кулі і площини у просторі.
Як можуть розміщуватися в просторі куля і площина ?
Можливі 3 випадки (d- відстань від центра кулі до площини, r- радіус кулі)-мал. 193:
- Площина і куля не мають спільних точок (r<d) - мал. а;
- Площина і куля мають безліч спільних точок (r>d) - мал. б;
- Площина і куля мають одну спільну точку (площина називається дотичною до кулі). Спільна точка площини і кулі називають точкою дотику. (r =d) - мал. в;
Пряму, що містить діаметр кулі, вважають віссю симетрії кулі.
(Чим ближче переріз розташований до центра кулі, тим він більший (більше його радіус).
Площина, дотична до кулі, перпендикулярна до радіуса, проведеного в точку дотику.
- Теорема про переріз кулі.
Дослідження. Переріз кулі площиною.
(розглянемо на прикладі апельсина і аркуша картону).
- Уявлення про яке тіло нам дає апельсин? А аркуш картону?
- Відтинаємо сегмент - це частина кулі.
Площина перетинає кулю по кругу.
- Уявлення про яке тіло нам дає шкірка апельсина?
- Давайте подивимось, по якій фігурі перетнула площина шкірку апельсина (по кругу чи по колу)?
Площина перетинає сферу по колу.
Теорема. Будь – який переріз кулі площиною є круг. Центр цього круга – основа перпендикуляра, опущеного з центра кулі на січну площину.
Наслідок. Будь – який переріз сфери площиною є коло. Центр цього кола є основою перпендикуляра, опущеного з центра сфери на січну площину.
- Означення діаметральної площини.
Діаметральна площина – це площина, яка проходить через центр кулі . Переріз кулі діаметральною площиною - це великий круг, а переріз сфери – велике коло.
( продемонструвати на апельсині.)
- Формула для обчислення площі сфери.
Площу сфери обчислюють за формулою :
S=4πR2 =πd2.
Площі двох сфер відносяться як квадрати їх радіусів або діаметрів.
|
Встановити логічні пари: 1.Геометрична фігура, що складається з усіх точок площини, рівновіддалених від однієї точки цієї площини. ______________________ 3.Тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану …
2.Геометричне тіло, що утворюється від обертання круга навколо діаметра… _______________________ 4. Геометрична фігура, яка утворюється від обертання кола навколо діаметра ... ______________________ 5. Поверхня, яка складається із всіх точок простору, що знаходяться на даній відстані від даної точки … |
|
А) Куля
Б) Коло
В) Сфера
Г) Круг
Д)Інша відповідь
КУЛЯ
СФЕРА
Встановити відповідні пари:
|
1.Довжина кола … 2.Діаметр кола… 3.Площа круга … 4.Довжина півкола … 5Подвоєна площа круга … А) 2R Б) 2πR B) πR2 Г) 2πR2 Д)Інша відповідь |
|
В прямокутному трикутнику… 1. Відношення прилеглого катета до гіпотенузи … 2. Відношення протилежного катета до гіпотенузи 3. Відношення протилежного катета до прилеглого …
4. Відношення прилеглого катета до протилежного … 5. Відношення сторони трикутника до синуса протилежного кута
А) 2R Б)sinα B)cosα Г) tg α Д) ctgα Колаж «Куля» Чи можна з дерев’яного циліндра, діаметр основи якого дорівнює 11 см, а висота 8 см, виготовити кулю радіуса 5 см? Так. Ні. (підкреслити). Радіус кулі дорівнює 4 см. Площа великого круга………….см2
Переріз кулі площиною - це ……………… Найбільша хорда кулі називається …………………… Куля утворюється обертанням …………. навколо його …………………… _______________________________________________
Колаж «Сфера» Яка фігура утворюється при перетині двох сфер? ……………………. Довжина великого кола дорівнює 12π см. Радіус сфери = ………см. Сфера – це …………………….. кулі. Переріз сфери площиною – це …….. Кінці діаметра називають …………………………………. точками.
Радіус кулі дорівнює 2,5 см. Визначити розміщення точки, якщо вона віддалена:
Відповідності: А -…….. Б -……… В - …….. |
-
Круті задачі із пропущеним реченням, для дітей із середнім рівнем знань або на початку вивчення теми для всіх- це спасіння!


про публікацію авторської розробки
Додати розробку