Урок з геометрії в 11-му класі.

Розроблено та проведено 

вчителем математики ЗОШ № 7 ім. В. В. Бражевського м. Житомира

Сергієм Олександровичем Сафонюком

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                 

Актуалізація опорних знань, вмінь та навичок учнів, набутих ними при вивченні теми: "Об’єми тіл".

Завдання на відповідність

 

Правильні відповіді

Знання формул та вміння використовувати їх допомагають розв’язувати задачі, які начебто не мають зв’язку з геометрією. 

Розглянемо декілька таких задач.

Задача № 1

 

 

 

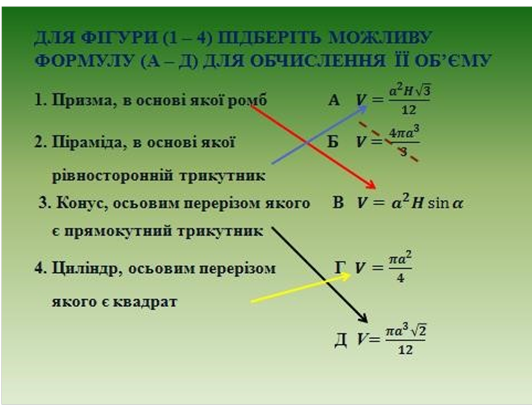
Складемо геометричну модель цієї задачі. Сформулюємо цю проблему інакше. Так як маса тіла залежить від об’єму та густини, то необхідно знайти об’єм тіла, яке обмежене двома циліндрами з радіусами основ 0,71 м і 0,688 м та висотою 4450000 м.

                                                 Дано: циліндр з радіусом R₁ = О₁А₁ = 0,71 м,            О₁                     А₁ циліндр з радіусом  R₂ = OA = 0,688 м висота Н = О₁О = 4450000 м                                                  Знайти:  V тіла, обмеженого циліндрами

Розв’язування

                                           𝑉 = 𝑉_𝑅1 − 𝑉_𝑅2 = 𝐻𝜋(𝑅₁² − 𝑅₂²)

𝑉 = 4450000 ∙ 3,14 ∙ (0,71² − 0,688²) ≈ 429753,6 (м³) З курсу фізики відомо, що 𝑚 = 𝑉 ∙ 𝜌.

            О А          Отже, 𝑚 = 429753,6 ∙ 7600 ∶ 1000 ≈ 3266127,36 (т).

Відповідь: 3266127,36 т

 

 

 

Задача № 2

 

 

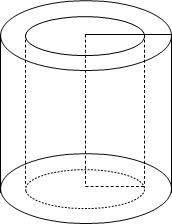
Представимо дріт у вигляді циліндра з радіусом основи 0,003 м. Висота цього циліндра і буде довжиною дроту, яку необхідно знайти.

Дано: циліндр з радіусом ОА = R = 0,003 м

О             А                         m = 30 кг, 𝜌 = 7600  

 Знайти: Н

Розв’язування

Щоб знайти висоту циліндра, необхідно                                                             знайти його об’єм.

З курсу фізики відомо, .

З іншого боку 𝑉 = 𝑆_𝑜 ∙ 𝐻 = 𝜋𝑅²𝐻.

Прирівнюємо праві частини рівностей

                                                              м

                        Відповідь: 139,7 м

Задача № 3

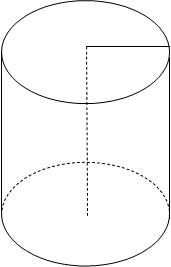
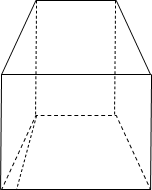
Представимо цей насип у вигляді прямої призми, в основі якої лежить трапеція з основами 8 м і 18 м та висотою 3 м. Висота призми 1000 м. Знайдемо об’єм цієї фігури.

 

       В₁ С₁                             Дано: ABCDA₁B₁C₁D₁ – пряма призма

AD = 18 м, BC = 8 м, АА₁ = 1000 м

ВК – висота, ВК = 3 м

Знайти: V

А₁ D₁                             Розв’язування

В                    С                                 𝑉 = 𝑆₀ ∙ 𝐻

 

 

 А D                       Відповідь: 39000 м³

      К

    

 

 

 

 

 

Задача № 4

 

 

Розв’язування

                                1 га = 10000 м², тоді 5,3 га = 53000 м².                                  

                                 

Відповідь: 2597000 м³.

Ось так життєві ситуації та проблеми ми перевели на мову математики, що дозволило нам розв’язати задачі прикладного змісту.