Розробка уроку "Лінійні рівняння з однією змінною"

Урок №5.

ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ

Мета: поглибити, розширити й узагальнити відомості про види рівнянь та способи їх розв’язування; домогтися свідомого розуміння змісту поняття «лінійне рівняння з однією змінною» та схеми розв’язування лінійних рівнянь.

Тип уроку: систематизація та поглиблення знань.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

1. Математичний диктант

1) Обидві частини рівняння помножили на –3 [поділили на 7]. Що можна сказати про вихідне і здобуте рівняння?

2) Доданок –3 [7] перенесли з правої в ліву частину рівняння, замінивши знак – [+] на +[–7]. Якими є вихідне і здобуте рівняння?

3) Закінчіть речення:

«Рівняння і є рівносильнимиу, бо ...» [«Рівняння і є рівносильними, бо ...»]

4) Розв’яжіть рівняння:

.

Щоб простіше було перевіряти й оцінювати роботу учнів, відповіді в зошитах записуємо у вигляді таблиці:

№ завдання	Відповідь	Корекція

 

2. Якість виконання вправ домашнього завдання перевіряємо, зібравши зошити (№ 3 пояснюємо окремо).

ІІІ. Актуалізація опорних знань

Виконання усних вправ

1) Обчисліть: ; ; ; .

2) Спростіть вираз:

а) ; б) ; в) ; г) .

IV. Повторення, поглиблення та систематизація знань

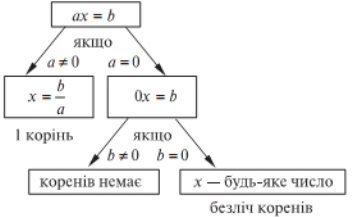
Поняття лінійного рівняння з однією змінною є принципово новим для учнів (новим є і сам підхід до класифікації не за дією, що зв’язує компоненти рівняння, а за способом розв’язування).

Хоча фактично всі рівняння, що їх розв’язували учні в молодших класах, є рівняння, що зводяться до лінійних, однак відповідна термінологія вводиться вперше. Під час дослідження питання про кількість розв’язків лінійного рівняння при різних і виділяємо три випадки:

1) і будь-яке;

2) ; ;

3) ; .

Із першим випадком учні вже зустрічались, другий і третій є для них новими. Переходячи від теоретичного матеріалу до розв’язування рівнянь із застосовуванням названих вище міркувань, треба пояснити (показати на прикладах), в якому випадку ми дістаємо рівняння виду , бо дуже часто учні не розуміють, як і чому під час розв’язування рівняння, наприклад, ми дістаємо рівняння і найголовніше: мотивація (з неї і слід почати цей етап уроку). На багатьох прикладах різних видів рівнянь треба показати, що лінійні рівняння є основою цих рівнянь.

План викладення матеріалу

1. Робота з випереджальним домашнім завданням (мотивація).

2. Означення лінійного рівняння з однією змінною.

3. Схема розв’язування лінійних рівнянь з однією змінною.

4. Приклади рівнянь, що зводяться до лінійних і схема їх розв’язування.

Результатом обговорення можуть бути такі записи в зошитах учнів:

Конспект 2

Лінійні рівняння з однією змінною

1. Розв’язуючи рівняння, під час рівносильних перетворень ми дістаємо рівняння, що можна записати в одному вигляді, якщо записати числа буквами, а саме: .

2. Рівняння виду , де і — числа, а — невідоме, називається лінійним рівнянням з одним невідомим.

Наприклад: ; ; ; ; ; .

3. Схема розв’язування лінійного рівняння виду .

 

4. а) ;	б) ;	в)
Шляхом рівносильних перетворень зводимо рівняння до виду , а далі за схемою:
; ; ; ; Відповідь. -3	; ; ; Відповідь. Коренів немає	Відповідь. — будь-яке число

 

Зауважимо: 1) Під час розв’язування рівняння при поширеною є така помилка учнів: спроба знаходження як частки у вигляді цілого числа або десяткового дробу (часто чуємо, що не розв’язується, бо ). Тому, застосовуючи алгоритм, наголошуємо, що при корінь — існує завжди, не залежно від співвідношення та , і може бути як натуральним, так і цілим числом або дробом — звичайним чи десятковим. Але, щоб не виконувати зайвих дій, (окрім випадків, коли ділення найкраще виконується усно) корінь треба записувати спочатку саме як дріб, а потім вже використовувати набуті в 6 класі вміння перетворювати дроби.

2) У прикладах 4 (б, в) дуже важливо, щоб учні зрозуміли, звідки береться у лівій частині лінійного рівняння. Тому актуалізація знань (див. вище) є дуже важливим елементом уроку.

V. Закріплення знань, формування вмінь

Однією з програмних вимог до рівня загальноосвітньої підготовки учнів є вміння розпізнавати лінійні рівняння серед даних рівнянь, наводити приклади лінійних рівнянь та розв’язувати лінійні рівняння з однією змінною та ті, що до них зводяться.

Тому в системі завдань до уроку бажано виділити завдання таких типів:

1) на розпізнавання лінійних рівнянь та на складання лінійних рівнянь за певними умовами;

2) на розв’язування лінійного рівняння та простіших рівнянь, що зводяться до лінійних шляхом рівносильних перетворень.

1. Виконання усних вправ

1. Які з рівнянь є лінійними:

; ; ; ; ; ; ; ?

2. Складіть будь-яке рівняння виду , коренем якого є число 3; число 0.

3. Скільки коренів мають рівняння: ; ; ?

4. Знайдіть корінь рівняння:

; ; ; ; ; .

Виконання письмових вправ

Розв’яжіть рівняння:

1. 1) ;

2) ;

3) ;

4) ;

5) ;

6) .

2. 1) ;

2) ;

3) .

3. 1) ;

2) ;

3) ;

4) .

4. 1) ;

2) .

5*. При якому значенні :

1) значення виразу дорівнює –4;

2) вирази і мають рівні значення;

3) значення виразу на 7 більше за значення виразу ?

VI. Підсумок уроку. Рефлексія

1.Яке з рівнянь є лінійним з однією змінною (, — числа)

а) ; б) ; в) ; г) ?

2. В якому випадку немає коренів у рівнянні

а) ; ;

б) ; ;

в) ; ;

г) ; ?

3. В якому випадку рівняння має один корінь? В якому випадку немає коренів у рівнянні ?

а) ; ;

б) ; ;

в) ; ;

г) ; .

VII. Домашнє завдання

№ 1. Розв’яжіть рівняння:

1) ;

2) ;

3) ;

4) .

№ 2. Відшукайте корінь рівняння:

1) ;

2) ;

3) .

№ 3 (випереджальне). Користуючись підручником, знайдіть значення , при яких виконуються рівності:

а) ; б) ; в) .

За розв’язаннями з’ясуйте, скільки коренів може мати рівняння з модулем виду , залежно від знака , де — число.