Розробка уроку на тему: Дробові числа. Звичайні дроби. Розв'язування задач.

5 клас

ТЕМА: 1. Дробові числа. Звичайні дроби.

2. Розв'язування задач.

МЕТА: Сформувати поняття дробових чисел, звичайних дробів; сформувати вміння читати і записувати звичайні дроби.

Сприяти розвитку уваги, пам'яті, логічного мислення;

Виховувати вміння працювати самостійно із підручником.

ТИП УРОКУ: урок засвоєння нових знань, умінь і навичок.

ОБЛАДНАННЯ ТА НАОЧНІСТЬ: педагогічний програмний засіб, роздатковий матеріал.

Хід уроку

І. Організаційний момент.  Заходжу до класу, вітаюсь з учнями, пропоную їм сісти. Мовчки оглядаю готовність учнів до уроку (чи всі сидять за робочими місцями; наявність підручника, зошита, чорновичка, ручки, олівця, лінійки)

II. Мотивація навчання

З історії звичайних дробів

Першим дробом, який почали використовувати люди, був, напевно, дріб -, що характеризував половину мисливської здобичі, половину деякої міри зерна, половину даної відстані тощо. За дробом - з'явились дроби, пов'язані з поділом на дві рівні частини половини, а потім четвертини тощо. Такі дроби називають двійковими.  У  Стародавньому Вавилоні використовували шістдесяткові дроби. Із цими дробами пов'язаний теперішній поділ години на 60 хвилин, а хвилини — на 60 секунд.

У Стародавньому Єгипті дробами оперували ще 4000 років тому. Проте загальної форми запису дробів, як це прийнято тепер, у єгиптян не було. Запис дробів за допомогою риски став загальноприйнятим у XVI столітті.

Крім необхідності подрібнення цілого на частини, появу дробів обумовлювали також потреби вимірювання. Коли одиниця вимірювання не вкладалась у величині, що вимірюється, ціле число разів, то цю одиницю вимірювання ділили на кілька рівних частин, отримуючи нову, меншу, одиницю вимірювання.

У Київській Русі дроби називали частинами.

ІІІ. Актуалізація опорних знань, підготовка до сприйняття нового матеріалу.

Колективне розв’язування вправ.

1) Накресліть відрізок довжиною 6 см. Поділіть його на 3 рівних частини. Виділіть одну з цих частин іншим кольором.

ІV. Вивчення нового матеріалу.

Розріжемо яблуко на дві рівних частини і візьмемо одну з них.

Скажемо, що взяли половину, або одну другу яблука, і запишемо: одна друга ().

Якщо візьмемо дві половини, то матимемо дві других і запишемо: дві других ().

Розріжемо кавун на три рівні частини і візьмемо одну з них. Скажемо, що взяли одну третю, і запишемо:  одна третя ().

Якщо візьмемо дві такі частини, то матимемо дві третіх кавуна, запишемо:  дві третіх ().

Візьмемо відрізок. Поділимо відрізок на чотири рівні частини. Одна така частина — це  одна четверта (), три такі частини – три четвертих ().

Числа одна друга, дві других, одна третя, дві третіх, одна четверта, три четвертих називають дробовими. Вони записані звичайними дробами. Звичайні дроби записують за допомогою двох натуральних чисел і горизонтальної риски. Ця риска означає ділення цілого на кілька рівних частин.

1/2, 2/2 1/3 ... – дробові числа.

Число, записане під рискою, називають знаменником дробу. Знаменник дробу вказує, на скільки рівних частин поділено одиницю (ціле).

Число, записане над рискою, називають чисельником дробу. Чисельник дробу вказує, скільки взято рівних частин одиниці (цілого).

Ціле яблуко складається із двох половинок. Якщо візьмемо дві половинки яблука, тобто дві других яблука, то матимемо ціле яблуко. Отже, дві других = 1.

Три третіх кавуна — це цілий кавун, тобто три третіх = 1.

Чотири четвертих одиниці — це одиниця, тобто чотири  четвертих = 1.

Аналогічно п’ять п’ятих дорівнює одиниці,

шість шостих = 1

і так далі.

Поміркуємо, як розділити порівну 2 яблука між трьома учнями.

Якщо потрібно розділити два яблука порівну між трьома учнями, то кожне яблуко можна розрізати на три рівні частини.

Матимемо всього шість третин. Один учень одержить дві третини яблука.

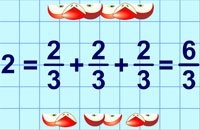
Отже, якщо два яблука розділити порівну між трьома учнями, то кожний з них одержить дві третіх яблука. Це можна записати так:

2 поділити на 3 = дві третіх.

Частка від ділення числа 2 на число 3 дорівнює дробу, чисельником якого є 2, а знаменником – 3.

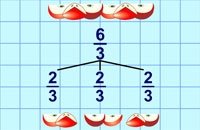
Частка від ділення одного числа на інше дорівнює дробу, чисельник якого дорівнює діленому, а знаменник — дільнику.

Наприклад, один поділити на чотири = одна четверта, 10 поділити на 2 = десять других.

Оскільки 10 поділити на 2 = 5, то десять других = 5.

Натуральне число 5 записане у вигляді дробу десять других, однак його можна записати також у вигляді інших дробів, а саме: 5 = п’ять перших, п’ять = 15 третіх, 5 = 20 четвертих і так далі.

1 : 4 =,      10 : 2 =

,     5=,      5=,     5=

Очевидно, що й кожне інше натуральне число можна записати у вигляді дробу, до того ж, багатьма способами.

V.  Закріплення отриманих знань.

1. Розглядаємо всі разом в підручнику, як виконуються вправи з рубрики „Виконаємо разом!”: № 1, 2
2. Закріплюємо новий матеріал, виконуючи усно вправи:  № 951, 952, 953.
3. Розв’язуємо   №963, 965, 968, 969, 975, 977.
4. Кращі учні, за бажанням, утворюють групу, в якій працюють над розв’язанням № 767.

V. Підсумок уроку

Повторення основних понять, які було розглянуто на уроці.

VІ. Домашнє завдання

§ 21 опрацювати.

Розв’язати: №964, 967, 976, 983.