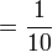Тема: Поняття звичайного дробу
Конспект уроку в 5 класі
Тема: Поняття звичайного дробу
Мета: розширити знання учнів про звичайний дріб, сформувати поняття чисельника та знаменника дробу; розвивати логічне мислення при розв’язуванні вправ.
Тип уроку: урок засвоєння нових знань.
Обладнання: комп’ютер, презентація «Поняття звичайного дробу».
Хід уроку
- Організаційний момент.
Вчитель вітається з класом. Налаштовує клас на роботу на уроці.
- Мотивація навчальної діяльності.
Вчитель. Ви вже знаєте, що крім натуральних чисел та нуля,є ще дробові числа. З дробовими числами ви знайомилися ще в початковій школі. Ви знаєте дріб як частину від цілого. Сьогодні ми пригадаємо, що ж таке дробове число, а на наступних уроках будемо вивчати дії над дробовими числами.
Дроби мають широке застосування в повсякденному житті. Ми використовуємо, наприклад такі слова як половина, третина; звертаємося в магазині «Дайте півкілограма цукерок». Отже, вивчення звичайних дробів необхідне для використання отриманих знань в повсякденному житті.
Необхідність в дробових числах виникла у людей на ранніх стадіях розвитку. Поділ здобичі, який складався з декількох вбитих тварин, між мисливцями, якщо число тварин виявлялося не подільним кількості мисливців, мало привести первісну людину до поняття про дробове число.
З виникненням уявлень про цілі числа виникали уявлення і про частини одиниці, точніше, про частини цілого конкретного предмета. Так, виникнення уявлення про число «два» зумовлювало уявлення про «половину», про «половину половини» і т. д. З появою натурального числа п виникло уявлення про дріб виду ![]() .
.
Поява звичайних дробів дуже характерна для початкового розвитку поняття числа в стародавній цивілізації. Вона зумовлена процесом подрібнення цілого на частини. Потреба в точних вимірюваннях привела до того, що початкові одиниці мір почали ділити на 2, 3 і більше частин. Дрібнішій одиниці міри, яку діставали внаслідок такого поділу, надавали індивідуальної назви і величини вимірювали вже цією дрібнішою одиницею. Так виникли перші конкретні дроби.
Пізніше ми ще познайомимося з історією дробів.
- Актуалізація опорних знань.
Вчитель. Отже, ви вже знайомі з дробовим числом, також вам відомі чисельник та знаменник дробу. Ви розглядали задачі на знаходження частки числа і задачі на знаходження числа за його часткою.
Давайте розглянемо задачу на знаходження частки числа усно.
Слайд 1-2.
Задача. Від смужки довжиною 15 см відрізали її третю частину. Скільки сантиметрів відрізали від смужки?
Вчитель вислуховує думки учнів. Узагальнює і записує розв’язання на дошці.
15 см : 3 = 5 см – третя частина смужки.
Давайте розглянемо задачу на знаходження числа за його часткою.
Слайд 3.
Задача. Хлопчик відрізав від смужки 4 см, що становить третю частину від усієї смужки. Яка довжина всієї смужки?
Вчитель вислуховує думки учнів. Узагальнює і записує розв’язання на дошці.
4 см ![]() 3 = 12 см – довжина всієї смужки.
3 = 12 см – довжина всієї смужки.
- Повідомлення теми, мети і завдань уроку.
Тема нашого уроку «Поняття звичайного дробу». Метою нашого уроку є розширити ваші знання про звичайний дріб. Слайд 4.
- Сприймання та первинне усвідомлення нового матеріалу.
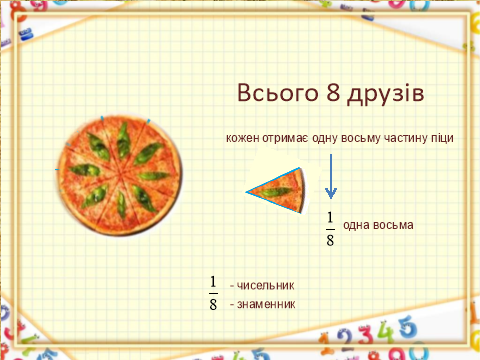
Вчитель. Розглянемо такий приклад. Нехай до Оленки прийшли у гості сім друзів. Оленка вирішила пригостити друзів піцою. Мама Оленки розділила піцу на 8 частин. Скільки частин отримає кожний з дітей?
Учні коментують задачу. Потім отримують результат, що кожен отримає одну восьму частину піци.
Слайд 5.
Вчитель. Одну восьму можна записати за допомогою чисел, а саме ![]() .
.
Такий запис використовують і для інших дробових чисел. Наприклад, півпирога - ![]() , читають «одна друга пирога», третина шляху -
, читають «одна друга пирога», третина шляху - ![]() читають «одна третя шляху».
читають «одна третя шляху».
Якщо хтось з Оленчиних гостей не захоче піци, то комусь дістанеться ![]() піци.
піци.
Записи виду ![]() та інші називають звичайними дробами або просто дробами. Звичайні дроби, як ви вже помітили записують за допомогою двох натуральних чисел і риски дробу. Число, записане над рискою, називають чисельником дробу, число записане під рискою, називають знаменником дробу.
та інші називають звичайними дробами або просто дробами. Звичайні дроби, як ви вже помітили записують за допомогою двох натуральних чисел і риски дробу. Число, записане над рискою, називають чисельником дробу, число записане під рискою, називають знаменником дробу.
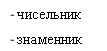 Запис на дошці:
Запис на дошці:
![]()
Давайте на нашому прикладі з’ясуємо, що показує знаменник та чисельник у дробі ![]() .
.
Відповідь учнів. Знаменник показує, на скільки частин розділили піцу, а чисельник показує, скільки частин отримав кожен з друзів.
Вчитель. Спочатку існували тільки двійкові дроби. Пізніше до цих дробів було приєднано ![]() та її двійкові поділи.
та її двійкові поділи.
У зв'язку з діленням різних одиниць вимірювання на частини на Русі були дуже поширені дроби виду: половина ![]() , чверть
, чверть ![]() , півчверть
, півчверть ![]() , пів-півчверть
, пів-півчверть ![]() , пів-пів-півчверть або мала чверть
, пів-пів-півчверть або мала чверть ![]() , третина
, третина ![]() , півтретина
, півтретина ![]() , пів-півтретина
, пів-півтретина ![]() , пів-пів-півтретина, або мала третина
, пів-пів-півтретина, або мала третина ![]() і т. д. Слайд 6.
і т. д. Слайд 6.
Однією з перших відомих згадок про єгипетські дроби є Математичний папірус Рінда. Три більш давні тексти, в яких згадуються єгипетські дроби — це Єгипетський математичний шкіряний сувій, Московський математичний папірус і Дерев'яна табличка Ахміма.
![]()
![]() Слайд 7. Дроби мали своє позначення (знаки), дріб
Слайд 7. Дроби мали своє позначення (знаки), дріб ![]() позначали
позначали![]() , всі інші виражалися за допомогою символа «ро», який мав вигляд . Щоб зобразити певний дріб малювали цей символ і під ним ставили число, яким є знаменник. Наприклад,
, всі інші виражалися за допомогою символа «ро», який мав вигляд . Щоб зобразити певний дріб малювали цей символ і під ним ставили число, яким є знаменник. Наприклад, ![]() записувалась так .
записувалась так .
Наприклад:
|
|
|
|
Спеціальні символи для дробів ![]() , якими можна було записувати також інші дроби (більші ніж 1 / 2).
, якими можна було записувати також інші дроби (більші ніж 1 / 2).
|
|
|
|
|
|
У Греції дроби широко застосовувалися не пізніше V ст. до н. є. Греки вільно оперували всіма арифметичними діями з дробами, але за числа їх не визнавали.
Починаючи з II ст. до н. е., а можливо навіть і трохи раніше, александрійські математики почали широко користуватися також єгипетськими дробами і відповідною технікою лічби.
Єгипет, Вавілон і Рим незалежно один від одного створили своєрідне вчення про дроби.
Дроби у народів Китаю з'явилися майже одночасно з цілими числами. Першими дробами в них були ![]() які називаються «половиною», «малою половиною» і «великою половиною».
які називаються «половиною», «малою половиною» і «великою половиною».
У індійського математика Брахмагупти (598-бл. 660) знаходимо досить розвинуту систему дробів. У нього зустрічаються різні основні і похідні дроби з будь-якими чисельниками. Чисельник і знаменник записували так само, як і в нас, але без горизонтальної риски — просто розміщували один над одним.
До XV—XVI ст. вчення про дроби набуло сучасного вигляду, і оформлюється приблизно в ті самі розділи, які вивчаються зараз.
Про походження дробів тоді часто не говорили або говорили дуже мало. Таким чином, хоча дробами й оперували ще народи стародавнього Сходу (Єгипту, Вавілону), однак чітке уявлення про дробові числа, як про числа абстрактні рівноправні з цілими, виникло тільки в XVI ст. у зв'язку з розвитком арифметики.
- Первинне застосування знань.
Давайте розв’яжемо декілька вправ на застосування отриманих знань.
Слайд 8.№ 651. (усно). За підручником Мерзляк А. Г., Полонський В. Б., Якір М. С., Математика: Підручник для 5-го класу. – Х.: Гімназія, 2005.
Прочитайте дроби: ![]() . Назвіть чисельник і знаменник кожного дробу і поясніть, що вони означають.
. Назвіть чисельник і знаменник кожного дробу і поясніть, що вони означають.
Учні по черзі читають дроби.
Слайд 9-10. Приклад 1. (письмово) Учні записують відповідь в зошити, а потім звіряють відповідь з відповідями на дошці.
Запишіть у вигляді дробу число:
- одна третя;
- дві п’ятих;
- шість одинадцятих;
- двадцять тридцятих;
- тридцять чотири сорок других;
- сто вісімнадцять сто двадцять сьомих;
- триста двадцять шостих тисячних.
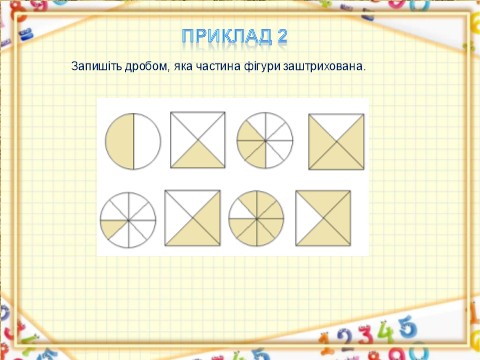
Слайд 11. Приклад 2. Запишіть дробом, яка частина фігури заштрихована.
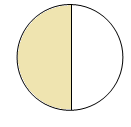
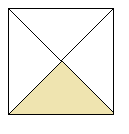
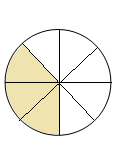

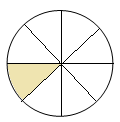
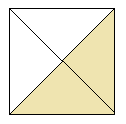
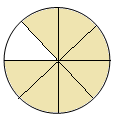
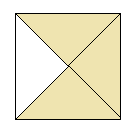
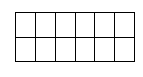
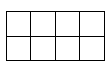
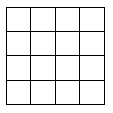
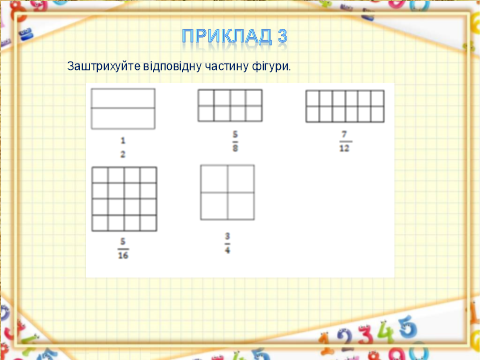
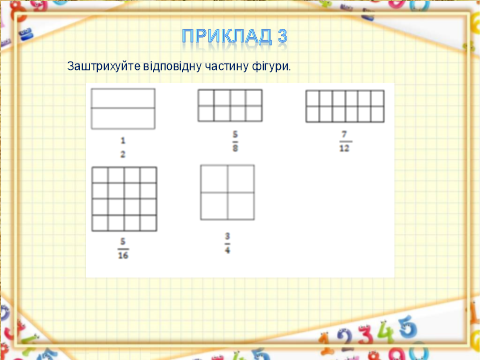
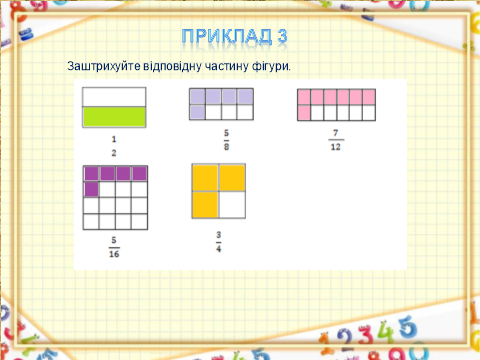
Слайд 12-13. Приклад 3. Заштрихуйте відповідну частину фігури. (Учням вчитель роздає завдання на картках)
Картка

![]()
![]()
![]()

![]()
![]()
Слайд 14. № 655.(письмово)
Виразіть:
- у метрах: 1 см; 5 см; 24 см; 1 дм; 7 дм; 1 мм; 4 мм; 39 мм; 247 мм;
- у годинах: 1 хв; 7хв; 19 хв; 39 хв; 1 с; 4 с; 58 с.
Двоє учнів виходять до дошки виконувати завдання.
- Повідомлення домашнього завдання.
Вчитель. Відрийте щоденники та запишіть домашнє завдання, яке записане на дошці. Слайд 15.
§4. П. 22 (ст. 159-161). № 652, 656.
- Підбиття підсумків уроку.
Вчитель виставляє оцінки учням.













про публікацію авторської розробки
Додати розробку