Розробка уроку Прогресії. Розв'язування задач з різних предметних областей.

 

 

 

 

РОЗРОБКА УРОКУ

 

Інформатика 9 кл

тема:

« Прогресії навколо нас».

 

 

Підготувала:

вчитель інформатики, фізики                        

КЗ «Ширяївський ОК №1»

смт Ширяєве

               Недіна Л А А
І Мотивація: Легенда про Сета, автора гри «Шахи»

Гра  в шахи була придумана в Індії. Коли  індуський цар Шерам познайомився з цією грою, він був вражений її красою та  різноманітністю можливих  в ній  положень. Дізнавшись, що  ця гра придумана одним із його підданих, цар наказав його покликати, щоб особисто нагородити..

Винахідник гри, його звали Сет, прийшов до трону повелителя. Це був скромно одягнений вчений, який заробляв  на життя, навчаючи учнів науки.

- Я бажаю тебе достойно нагородити, Сета, за чудову гру, яку ти придумав – сказав цар. Вчений поклонився.

- Я достатньо багатий, щоб виконати твоє найсміливіше бажання, - продовжував цар. Називай нагороду, яку побажаєш, і ти отримаєш її.

Сета мовчав.

 - Не соромся,-  підбадьорив його цар.- Говори своє бажання. Я не пошкодую нічого, щоб виконати його.

- Безмежна твоя доброта, повелитель. Але дай мені час, щоб обдумати відповідь. Завтра я скажу тобі своє прохання.

На слідуючий день Сета прийшов до трону і дуже здивував царя безмежною скромністю свого прохання.

- Повелителю,  накажи видати мені за першу клітину шахової дошки одне пшеничне зерно.

- Просто пшеничне зерно? - здивувався цар.

- Так, повелителю. 3а другу клітину накажи видати 2 зерна, за третю 4, за четверту - 8, за п’яту - 16, за шосту - 32 ...

- Досить,- роздратовано мовив цар.­ Ти отримаєш свої зерна за всі 64 клітки, як бажаєш: за кожну вдвічі більше попередньої. Але знай, що прохання твоє  недостойне моєї щед­рості.  Бажаючи таку малу нагороду, ти не поважаєш мою милість.  Можеш іти, мої слуги винесуть тобі мішок з пшеницею.

Сета усміхнувся, залишив зал і став чекати біля воріт замку.

Під час обіду цар згадав про вченого і послав дізнатися, чи забрав безрозсудний Сета свою мізерну нагороду.

- Повелителю,- була відповідь,- твій  наказ виконується. Придворні математики рахують  ЧИСJIО потрібних зерен.  Цар нахмурився. Він не  звик, щоб його накази виконувалися так повільно.

Ввечері,  цар  знову поцікавився, чи давно Сета зі своїм мішком пшениці залишив палац. - Повелителю,- відповіли йому,- математики твої трудяться  і мають намір ще до ранку закінчити розрахунок.

- Чому так повільно? - розгнівався цар.- Завтра, перш ніж я прокинусь, все зерно повинно бути видано Сету. Я двічі не наказую.

Вранці до  повелителя на доклад прийшли всі математики з надзвичайно важливою інформацією.

Цар вийшов щоб вислухати старшого з математиків.

- Ми   обчислили всю кількість зерен, які хоче отримати  Сета. Число дуже - дуже велике ...

Яким би великим воно не було, перебив цар, мої житниці не стануть менші. Нагорода повинна бути видана….  

- Повелителю, ти не зможеш виконати подібне бажання. В усіх твоїх сховищах немає такої кількості зерна, які забажав отримати Сета. Немає їх і в житницях цілого царства. Не знайдеться стільки і на всьому  земному просторі. І, якщо ти бажаєш, повелителю, видати цю нагороду  то накажи перетворити всі моря та океани, ліси і гори в пахотні землі. Нехай ввесь цей простір засіють пшеницею, і все що вродить накажи віддати Сету. Можливо тоді він отримає свою нагороду.

З великим подивом слухав цар математика.

-Назви мені це дивовижно велике число, - промовив він

18 446 744 073 709 551 615

- Вісімнадцять квінтильйонів чотириста со­рок  шість квадрильйонів  сімсот сорок чотири  трильйони сімдесят три біліони сімсот дев’ять мільйонів  п’ятсот п’ятдесят одна тися­ча шістсот п’ятнадцать, о повелителю!

Кількість зернин, про які йдеться в задачі, є сумою 64 членів геометричної прогресії, у якої ,

=18446744073709551615, що приблизно становить 13,8 млрд. 40-тонних вагонів.

Якщо таку кількість зернин рівномірно розсипати по всій земній поверхні, то твориться шар пшениці товщиною 9-мм.

Тема уроку:  Прогресії навколо нас.

Тип уроку: урок-семінар.

Обладнання: комп’ютери, проектор, програма Miscrosoft Excel

Девіз: "...Математика безмежно різноманітна, як світ, і присутня, міститься в усьому."(М.П. Єругін).

“Числа не правлять світом, але вони показують, як управляється світ.”
       (Йоган Гете)

 

І. Постановка мети і завдань уроку

На сьогоднішньому уроці ми узагальнимо свої знання про прогресії, покажемо практичне застосування теми на прикладах задач із життя та історичних задач.

II. Актуалізація опорних знань учнів

Питання:

1. Що таке електронні таблиці? Програма, що моделює на екрані двовимірну таблицю  і дозволяє виконувати обчислення з даними цієї таблиці.
2. З якими електронними таблицями працюємо ми? Excel
3. Що таке маркер заповнення? Нижній правий куточок активної клітини.
4. Як виконати копіювання за допомогою маркера заповнення? Набрати дані в одній клітині і потім цю клітину потягнути  лівою кнопкою за маркер заповнення.
5. Як виконати заповнення  діапазону комірок датами за допомогою маркера заповнення? В першу комірку діапазону записати першу дату в форматі 05.03.2019, цю клітину потягнути за маркер заповнення правою кнопкою мишки і в меню, що з’явиться вибрати «Заповнити по датам»
6. Що таке формула в Excel?  Вираз, що починається зі знака =, набирається в англійському регістрі і  може містити адреси комірок, знаки математичних операцій, сталі величини, функції.
7. Що відбувається з формулою, якщо її перетягувати маркером заповнення?  Модифікується, тобто адреси комірок змінюються в залежності від комірки в яку потрапила  формула.
8. Що таке арифметична прогресія? (Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число: a₁, a₁+d, a₁+2d, a₁+3d, ... . 

Різницю арифметичної прогресії позначають буквою d.

Різницю арифметичної прогресії можна знайти, якщо від будь-якого члена прогресії, починаючи з другого, відняти попередній. d = a_n+1 – a_n , тобто  d = a₂ - a₁ = a₁₀ – a₉

9. Що таке геометрична прогресія?( Геометричною прогресією називається така числова послідовність 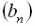, кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те ж саме стале для даної послідовності число, відмінне від нуля. 

Або це послідовність чисел, перший член якої не дорівнює нулю, а відношення будь-якого елемента послідовності до попереднього є сталим числом, що називається знаменником прогресії. Знаменник прогресії не дорівнює 1 (одиниці) Якщо модуль знаменника прогресії більше одиниці — прогресія зростаюча, якщо він менше одиниці — прогресія спадна. У випадку коли знаменник прогресії менше нуля — прогресія знакозмінна.

Значення n-ного члена

Позначимо перший член b₁, а знаменник прогресії q. Тоді другий член

b₂= b₁* q, третій — b₃= b₂* q= b₁* q², четвертий — b₄= b₃* q= b₁* q³, і так далі.

Тому вираз n-ного члена буде: b_n= b₁q^n-1

III. Історична довідка

Прогресія - явище без перебільшення, унікальне. Історія виникнення прогресії сягає глибини віків.

Підсумовуванням арифметичних і геометричних прогресій та складанням відповідних задач займалися багато любителів математики протягом багатьох століть.

Перші задачі на прогресії пов'язані із запитами господарського життя  (розподілу спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ. Так, у вавілонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п'яти днів відбувається за законом геометричної прогресії зі знаменником 2, у наступні 10 днів - за законом арифметичної прогресії з різницею 16.

 За законом геометричної прогресії здійснюється поділ нейтронів під час ядерної ланцюгової реакції. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію. Геометрична прогресія відіграє велику роль у побудові математичних моделей економіки. Знання прогресій потрібні і в багатьох інших галузях.

IV. Пояснення вчителя.

В Microsoft Excel є можливість дуже швидко і ефективно створювати арифметичну та геометричну прогресії.

Арифметична прогресія. Алгоритм створення.

1 Набрати перше число прогресії в першу комірку.

2 Набрати друге число прогресії в другу комірку.

3 Виділити обидві клітини і потягти  маркер заповнення  лівою кнопкою миші до необхідного значення. Значення поточного елемента підсвічується при перетягуванні маркера заповнення.

Геометрична прогресія. Алгоритм створення.

1 Набрати перше число прогресії в першу комірку.

2 Підхопити маркер заповнення правою кнопкою миші і потягнути на необхідну кількість комірок.

3 Відпустити праву кнопку миші  і в контекстному меню, що з’явиться вибрати пункт Прогресії.

4 Вказати тип прогресії, та її знаменник в полі Крок та клацнути на ОК

V. Розв'язування задач прикладного змісту

Зміст ряду історичних задач на прогресії, відбиває той подив, який викликало в тих, хто розв'язував ці задачі.

Розглянемо приклади таких задач:

Задача 1      Легенда про Сета, автора гри «Шахи»

Цю задачу розв’язує вчитель і показує на дошці, що за чим потрібно робити.

Розв’язок задачі:

Маємо геометричну прогресію перший член якої дорівнює 1, а знаменник прогресії дорівнює 2.

Будуємо в Excel геометричну прогресію для 64 членів і знаходимо їх суму.

1	1
2	2
3	4
4	8
5	16
6	32
7	64
8	128
9	256
10	512
11	1024
12	2048
13	4096
14	8192
15	16384
16	32768
17	65536
18	131072
19	262144
20	524288
21	1048576
22	2097152
23	4194304
24	8388608
25	16777216
26	33554432
27	67108864
28	134217728
29	268435456
30	536870912
31	1073741824
32	2147483648
33	4294967296
34	8589934592
35	17179869184
36	34359738368
37	68719476736
38	1,37439E+11
39	2,74878E+11
40	5,49756E+11
41	1,09951E+12
42	2,19902E+12
43	4,39805E+12
44	8,79609E+12
45	1,75922E+13
46	3,51844E+13
47	7,03687E+13
48	1,40737E+14
49	2,81475E+14
50	5,6295E+14
51	1,1259E+15
52	2,2518E+15
53	4,5036E+15
54	9,0072E+15
55	1,80144E+16
56	3,60288E+16
57	7,20576E+16
58	1,44115E+17
59	2,8823E+17
60	5,76461E+17
61	1,15292E+18
62	2,30584E+18
63	4,61169E+18
64	9,22337E+18
Сума	1,84467E+19

 

 

Задача 2.  Майбутнім біологам.

 

 За сприятливих умов деякі бактерії розмножуються так, що їх кількість  подвоюється кожну хвилину. Якщо на початку була одна бактерія, скільки їх буде через 3 хвилини? Через 10 хвилин?

 

Задача 3. Майбутнім філологам

Казка.

Як лисиця та вовк рибу дiлили. Вкрали лисиця з вовком риби багатенько, та й давай дiлитись. 

— Я не дуже тямущий у математицi, — каже вовк, — дiли ти, але так, щоб порiвну. 

— Ось тобi одна рибка, а менi двi, — каже лисичка. 

— Чи не замало?! — стривожився вовк. 

— Та нi, — каже лисичка, — слухай далi. Ось тобi три рибки... 

— Так можна, — заспокоївся вовк. 

— Менi 4, а тобi 5, менi 6, а тобi 7... 

Так дiлила лисичка рибку, щоразу збiльшуючи на одну рибину. Наостанку вона кинула собi

20 рибин i на цьому риба закiнчилась. Вовк подумав, що лисиця чесно подiлила. А ви як гадаєте, у кого бiльше риби i на скiльки?

 

Задача 4  Майбутнім фізикам.

Маємо деяку радіоактивну речовину масою 256 г, протягом доби її маса зменшується вдвічі. Якою буде маса речовини на другу добу?  На десяту добу?

 

Задача 5  Майбутнім лікарям

Кількість еритроцитів (з розрахунку на 1 мм3) в крові людини становить на рівні  моря – 5 мільйонів. Через кожні 600 м підняття вгору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори висотою 4800 м.

 

Задача 6. Майбутнім банкірам

Цікаво, яким буде ваш вибір?..

Уявіть собі, що ви опинились перед вибором: або отримати 100 000 доларів прямо зараз, або протягом 28 днів отримувати гроші, починаючи з  одного цента, при умові, що кожного наступного дня ця сума буде подвоюватись?

 

Задача 7 Майбутнім будівельникам

За 1 тиждень робітники побудували 5 поверхів будинку, а

потім було набрано додаткові бригади і за кожний наступний тиждень будували на 2 поверхи більше ніж за попередні. Скільки поверхів будинку побудували робітники за 6 тиждень; за 10 тиждень?

 

Учні розв’язують задачі за допомогою Microsoft Excel. Потім пояснюють розв’язання кожної задачі.

ЗАДАЧА , ЯКЩО ЗАЛИИВСЯ ЧАС

 

Задача . Уявіть, що вам деяка фірма пропонує свої послуги. Щодня ви можете брати у фірми по 100 грн. Але за перший день ви зобов'язані заплатити фірмі 1к, за другий - 2к, за третій - 4к. і т. д. Чи укладете ви з цією фірмою договір не менш ніж на 20 днів за таких умов?

Розв'язання:

Від фірми отримуємо - 2000 грн, а повинні будемо заплатити за це суму, що дорівнює 8го для геометричної прогресії, де . Тобто:

1048575(коп.)=10485грн. 75к

дні	Позика	Відсотки
1	100	0,01
2	100	0,02
3	100	0,04
4	100	0,08
5	100	0,16
6	100	0,32
7	100	0,64
8	100	1,28
9	100	2,56
10	100	5,12
11	100	10,24
12	100	20,48
13	100	40,96
14	100	81,92
15	100	163,84
16	100	327,68
17	100	655,36
18	100	1310,72
19	100	2621,44
20	100	5242,88
Всього	2000	10485,75

 

 

Вчитель робить зауваження, що в сучасних ринкових умовах учні повинні бути компетентними у фінансових питаннях, і тому освіченість особистості, як ніколи, на першому місці.

 

Вчитель. Як ми переконалися, прогресії застосовуються не тільки в математиці. За законом геометричної прогресії здійснюється поділ нейтронів під час ядерної ланцюгової реакції. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію. Геометрична прогресія відіграє велику роль у побудові математичних моделей економіки. Знання прогресій потрібні і в багатьох інших галузях.

 

V. Виконання тематичного тесту

Учні висловлюють свої враження від виступів, аналізують їх (відповідність темі, повнота розробки, краса та логіка викладу), вносять доповнення, роблять поправки.

 

VI. Підсумок уроку

Вчитель підсумовує учнівські виступи та доповнення до них, вказує на культуру математичного мовлення і мовлення взагалі, на лаконічність та ясність виступів та відповідей на запитання. Проводиться оцінювання учнів.

Висновок: Отже ми сьогодні

дізналися що таке прогресія та які вони бувають;

ми навчилися будувати прогресії в табличному процесорі  і використовувати їх для рішення задач;

 переконалися, що прогресії застосовуються не тільки в математиці, а в більшості галузей людської діяльності. За законом геометричної прогресії здійснюється поділ нейтронів під час ядерної ланцюгової реакції. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію. Геометрична прогресія відіграє велику роль у побудові математичних моделей економіки і так далі…

 "Прогресія", "прогрес", "прогресивний" - слова одного кореня. Прогресія - це послідовність, побудована за таким законом, який дає змогу продовжувати її необмежено, тобто рухатися вперед;

Бажаю, щоб у вашому житті завжди був рух тільки вперед, надіюсь що ви запам'ятаєте матеріал сьогоднішнього уроку і використаєте свої знання за необхідності.