Розв'язування стереометричних задач за допомогою програми для моделювання 3D графіки Google Sketch Up .

                                                           Анатолій Кральковський,

  вчитель математики

                                                              вищої категорії

 Лазарівської гімназії  

     Житомирського району

Розв'язування стереометричних задач за допомогою програми для моделювання 3D графіки Google Sketch Up .

 

В статті висвітлено питання  розв’язування стереометричних задач за допомогою програм для моделювання 3D графіки .

Постановка проблеми. Сучасні тренди у викладанні математики тісно пов’язані з використанням інформаційно-комунікаційних технологій. Тому неможливо недооцінювати роль ІКТ в розв’язуванні стереометричних задач з геометрії.

 В   процесі навчання математики задачі відіграють величезну й основоположну роль. Складність  розв’язування таких задач можна пояснити особливістю просторової уваги учнів та проблемою до відокремлення основного від другорядного.

Основним акцентом даної моделі розв'язування стереометричних задач є прикладна направленість, посилення міжпредметних зв’язків, урізноманітнення видів навчальної діяльності. Однією із важливих переваг даного методу є широке використання ІКТ на різних етапах вивчення теми з стереометрії.

Варто відмітити значний вплив використання прикладного програмного забезпечення для подальшої до профільної та профільної підготовки учнів. Формування навиків  розв’язування стереометричних задач, є досить кропітким та важливим елементом освітнього процесу. Складність розв’язування стереометричних задач та й геометричних задач в цілому, пов’язана зі складністю просторової уяви учнями.

      Питання  пошуку форм та методів розв’язування задач такого типу існує давно, як вчителів, так і методистів та вчених. Є багато цікавих розробок та новітніх методів. Але, не можна стверджувати, що це питання висвітлено повністю.

    

 

Мета статті. Ознайомити з методикою розв’язування стереометричних задач за допомогою програм для моделювання 3D графіки.

Виклад основного матеріалу. При переході до вивчення стереометрії в учнів часто виникають великі проблеми, особливо при розв’язуванні завдань на побудову в просторі. Учні відчувають великі труднощі при виконанні рисунків. Невміння зображати взаємне розміщення заданих точок, прямих і площин викликає розгубленість учнів, веде до хибних розв’язків. Тому варто зосередити увагу вчителів на методиці використання програм для 3D графіки на уроках математики для подолання проблем з просторовою уявою серед учнів.

 

Методика розв’язування стереометричних задач

(основні положення).

Розв'язування таких задач  служить досягненню  мети, виховання конкуренто-спроможного, компетентного випускника. Саме тому більшу частину уроків математики  слід присвятити  розв'язуванню задач та виконанню вправ тісно пов’язаних з життям. А стереометричні задачі це саме той випадок, що може тісно пов’язати навчання з будівництвом,  архітектурою, дизайном ландшафтів та інтер’єрів.

Розв'язуючи задачі, учні оволодівають найважливішими математичними поняттями, опановують математичну символіку, вчяться виконувати доведення тощо.

Крім того, математичні задачі можуть готувати до засвоєння нових теоретичних питань, допомагати закріпленню здобутих знань, ілюструвати практичні застосування вивченого матеріалу. У процесі розв'язування задач в учнів формуються навички розумової праці, а також важливі риси характеру: наполегливість, уважність, зосередженість.

Сформулюємо основні положення методики розв'язування стереометричних задач:

 

1.  На уроках стереометрії бажано більше навчати учнів розв'язувати задачі за зразками.

2.   Вчити учнів розв'язувати задачі доцільно за типами.

3.   Задачі кожного нового типу слід починати розв'язувати з найпростіших, поступово переходячи до складніших.

4.   Понад половини стереометричних задач доцільно розв'язувати з учнями усно.

5.  Для розвитку просторової уяви і графічної культури учнів на початку опрацювання кожної нової теми слід пропонувати вправи на малювання відповідних фігур.

6.  Малюнок в розв'язанні стереометричної задачі — не мета, а допоміжний засіб. Переважну більшість таких малюнків на класній дошці можна виконувати від руки.

7.  Кількості задач на обчислення, побудову, доведення і дослідження, пропонованих старшокласникам, повинні приблизно відноситись як 2:1:1:1.

8.   Значну увагу потрібно приділити колективній формі розв'язування задач у класі. (Якщо учень ще не навчився розв'язувати задачі того чи іншого типу, не слід пропонувати йому розв'язувати їх самостійно).

9.   Найвідповідальніші етапи в колективному розв'язуванні задачі — її вивчення і складання плану розв'язання. Не слід економити час за рахунок ущільнення цих етапів.

10.  Після розв'язування окремих задач бажано робити узагальнення, відмічати цікаві частинні випадки, виділяти групи подібних задач.

11.  Для деяких задач бажано пропонувати учням тільки виконати малюнок і скласти план розв'язання, не розв'язуючи задачу до кінця.

12.  Бажано максимально заохочувати пошуки різних способів розв'язання задач, знаходити серед них найраціональніші.

13.  До моделювання корисно звертатися тільки тоді, коли без цього учні не можуть правильно уявити зміст задачі.

14.  Самостійні роботи по розв'язуванню стереометричних задач не слід плутати з контрольними роботами. Основна мета самостійної роботи — навчати, удосконалювати уміння і навички учнів, а не контролювати.

15.  Більше уваги прикладним задачам.

16.  Менше формалізму в оформленнях розв'язань стереометричних задач, особливо на випускних екзаменах.

17.  Частіше пропонувати учням задачі на моделях.

Раціональна методика навчання розв'язуванню математичних задач відіграє істотну роль у формуванні високого рівня математичних знань, умінь і навичок учнів.

Джерело: Г. П. Бевз. «Методика розв'язування стереометричних задач». Київ 1988.

Неоцінене значення під час розв'язування стереометричних задач відіграють малюнки. Але малюнок тут — не мета, а тільки допоміжний засіб. Якщо учень може розв'язати задачу без малюнка, він може його й не виконувати. Складність стереометричних задач пов’язана з проблематичністю просторового уявлення умови задачі.

Деякі вчителі різні просторові фігури іноді зображають на частинах площини. В окремих випадках можна малювати не всю просторову фігуру, а її осьовий переріз або одну з кількох секцій, або лінію перетину фігур. Не обов'язково малювати всі вектори, про які йдеться в розв'язанні задачі. Замість кулі, вписаної або описаної навколо многогранника, можна малювати коло великого круга, а в деяких випадках — тільки центр і окремі точки її поверхні.

Я ж пропоную використовувати програмний продукт  Google Sketch Up, який не тільки полегшить розв’язування задач, а зробить їх цікавими та підсилить мотивацію під час вивчення математики.

Про те, як навчитись розв’язувати задачі, написано немало праць. У методичних посібниках подано загальні правила, поради, вказівки, які, на думку авторів, допомагають учням швидше навчитись розв’язувати задачі. Система порад, розроблена американським математиком Д. Пойа, найбільш відома, проте вона стосується всіх математичних задач, а тому досить загальна. Конкретнішою щодо геометричних задач є система порад Є. Ф. Данилової. Всього ця система містить 45 порад, що входять у такі шість груп:

 

Точно і чітко зрозуміти зміст задачі.

Скласти план розв’язування задачі.

Виконати план.

Обґрунтувати розв’язання.

Дослідити розв’язок.

Перевірити розв’язання.

 

Основне і найважче — скласти план розв’язування задачі. Є. Ф. Данилова в цій групі формулює 14 порад:

 

Розчленувати задачу на частини, якщо вона має кілька запитань.

З’ясувати, чи не є задача безпосередньо розв’язуваною.

З’ясувати, чи всі дані і шукані елементи введено в малюнок.

Шукати ідею розв’язання проведенням допоміжних ліній, пов’язаних з означеннями згаданих у задачі понять, і розкладаючи фігуру на трикутники.

Шукати ідею розв’язання за допомогою експерименту і розгляду малюнка.

З’ясувати, чи не можна замінити формулювання задачі іншим, зручнішим, а конкретну задачу — абстрактною геометричною.

З’ясувати, чи не можна перетворити дані, діставши з них наслідки.

З’ясувати, чи не можна уявити задачу розв’язаною і дістати в зв’язку з цим ряд наслідків.

З’ясувати, чи не можна скласти загальну формулу розв’язання задачі на обчислення або побудову.

З’ясувати, чи не можна перетворити шукані дані.

Розглянути окремі випадки, які вичерпують задачу.

З’ясувати, чи доводжуване твердження не є оберненим якому-небудь вже доведеному твердженню.

З’ясувати, чи не можна застосувати метод геометричних перетворень (симетрію, паралельне перенесення, гомотетію та ін.)

З’ясувати, чи не можна застосувати метод геометричних місць.

Безперечно, всі ці поради корисні. І вчитель, допомагаючи учням скласти план розв’язування задачі, може вести їх до мети саме такими короткими запитаннями: «Чи не можна розчленувати задачу на частини?», «Чи не можна скористатись гомотетією?» тощо. Зрозуміло, що кількість таких порад треба доповнити:

Чи не можна скористатись векторним методом?

Чи не можна скористатись координатним методом?

Чи не можна скористатись похідною, інтегралом?

Для задач окремих видів такі поради можна конкретизувати. Наприклад, навчаючи учнів розв’язувати задачі на побудову, корисно пропонувати:

Уявіть, якою може бути побудована фігура.

Виконайте ту частину побудови, яку можна виконати відразу.

Якщо площина перетинає паралельні площини, то лінії перетину паралельні!

Спробуйте скористатись методом слідів.

Спробуйте скористатись методом відповідності.

Спробуйте скористатись методом подібності.

Спробуйте скористатись алгебраїчним методом.

Зрозуміло, перш ніж давати учням такі поради, треба їх ознайомити з названими методами. І не слід переоцінювати роль таких порад. Щоб навчити учнів розв’язувати стереометричні задачі, перш за все, треба розв’язувати багато таких задач. Але якщо розв’язувати їх без системи, без узагальнень, без акцентування уваги учнів на окремих методах, на часто повторюваних прийомах, то бажаного результату досягти не можна.

 

Джерело: Г. П. Бевз. «Методика розв’язування стереометричних задач». Київ 1988.

 

Використання програмного забезпечення для проектування 3D графіки для розв’язування задач по стереометрії.

Google Sketch Up — програма для моделювання відносно простих тривимірних об'єктів — будівель, меблів, інтер'єру.

SketchUp можна використовувати для освітніх закладів на безоплатній основі з обліковим записом в G Suite и Microsoft Education.

  Створюючи рисунки до задачі за допомогою програмного забезпечення для проектування зD графіки ми отримуємо максимум інформації про умову задачі. Геометричні фігури можна обертати на 360⁰ . Це дає можливість побачити фігури з різних ракурсів. Крім того прозора заливка фігур дозволяє розглянути внутрішню будову та площини перерізів.

Google Sketch Up крім створення малюнків до задач дозволяє створювати елементи архітектури, дизайну кімнат, меблів, ландшафтного дизайну. Це додатково стимулює учнів до вивчення математики та створює умови для допрофільної та профільної підготовки.

GeoGebra — вільно-поширюване (GPL) динамічне геометричне середовище, яке дає можливість створювати «живі креслення» для використання в геометрії, алгебрі, планіметрії, зокрема, для побудов за допомогою циркуля і лінійки.

Крім того, програма володіє багатими можливостями для роботи з функціями (побудова графіків, обчислення коренів, екстремумів, інтегралів тощо) за рахунок команд вбудованої мови (яка, до речі, дає змогу керувати і геометричними побудовами).

 

 

 

 

Розв’язування стереометричних задач з використанням програмного забезпечення для проектування 3D графіки.

 

Тема уроку: « Стереометричні задачі на комбінацію геометричних тіл».

Мета уроку: ознайомити учнів з методами розв’язування задач з використанням ІКТ.

Тип уроку: комбінований.

Наочність і обладнання: персональний комп’ютер, програмне забезпечення для проектування 3D графіки.

Вимоги до рівня підготовки учнів: знають основні формули для просторових геометричних фігур та володіють алгоритмом їх застосування для розв'язування задач.

Хід уроку

І. Перевірка домашнього завдання

Фронтальне опитування

1)Сформулюйте формулу для знаходження площі бічної поверхні та об’єму  для довільної призми.

2)Як, користуючись цими формулами можна отримати формули для прямої призми, прямокутного паралелепіпеда та куба?

3) Сформулюйте формулу для знаходження площі бічної поверхні та об’єму правильної піраміди?

4)Сформулюйте формулу для знаходження площі бічної поверхні та об’єму зрізаної піраміди.

5)Сформулюйте формулу для знаходження площі бічної поверхні та об’єму основних тіл обертання?

Правильність виконання задачі з домашнього завдання перевірити за записами на дошці, зробленими до початку уроку.

 

 

ІІ. Додатковий теоретичний матеріал для розв’язування стереометричних задач.

1)Нехай в піраміді виконується одна з двох наступних умов:

а) всі бічні ребра утворюють з площиною основи рівні кути;

б) довжини всіх бічних ребр однакові.

Тоді вершина піраміди проектується в центр кола, описаного навколо основи піраміди ( ця ж точка є точкою перетину серединних перпендикулярів до сторін основи піраміди.

 

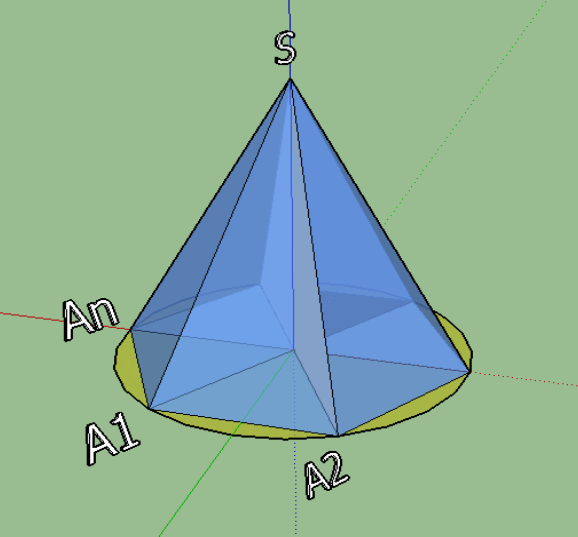
1.            Нехай в піраміді виконується одна з двох наступних умов:

а) всі бічні грані утворюють з площиною основи рівні кути;

б) довжини всіх апофем бічних граней рівні.

Тоді вершина піраміди проектується в центр кола, вписаного в основу піраміди ( ця ж точка є точкою перетину бісектрис кутів в основі піраміди.

2.            Якщо в похилій призмі бічне ребро А₁В₁ утворює рівні кути з сторонами основи_, що утворюють вершину А₁, то основа висоти В₁О точка О лежить на бісектрисі кута А₁.
3.            Якщо висота трикутної піраміди проходить через точку перетину висот трикутника, що лежить  в основі піраміди, то протилежні ребра піраміди перпендикулярні ( і навпаки).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ІІІ. Розв’язування задач на закріплення

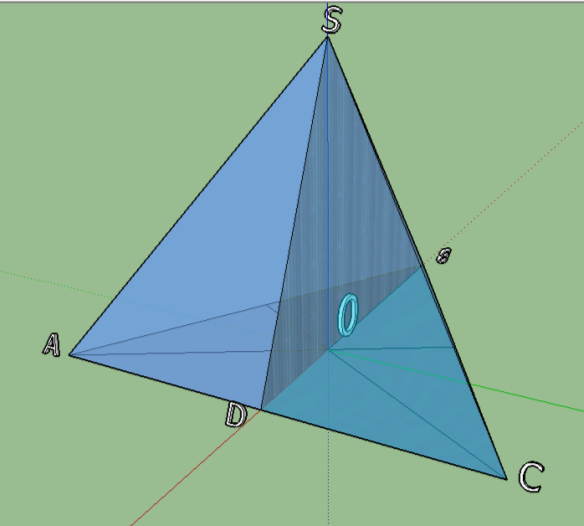
Задача 1.

 

Через медіану ВЕ основи АВС піраміди АВСD і середину ребра DС проведена площина. Знайти об’єм фігури ADBFE, якщо об’єм піраміди АBCD дорівнює 40см³.

Розв’язок.

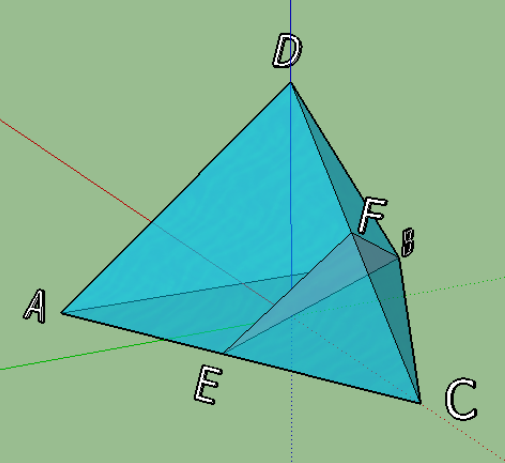
Об’єм фігури ADBFE дорівнює різниці об’ємів пірамід АВСD і ECBF. Щоб знайти об’єм піраміди ECBF, порівняємо його з об’ємом піраміди АВСD. Для цього достатньо знайти відношення площ їх основ і відповідних висот. Так як медіана трикутника ділить його площу на дві рівні частини, то S_∆BEC= S_∆ABC. Далі, так як F – середина ребра DC, то висота піраміди ECBF дорівнює половині висоти піраміди АВСD. Отже V _ECBF=V _АВСD=10 (см³).

 

 

Задача 2.

Висота циліндра дорівнює H, радіус його основи R. В циліндрі розміщено піраміду, висота якої співпадає з твірною АА₁ циліндра, а основою піраміди є рівнобедрений трикутник АВС (АВ=АС), вписаний в основу циліндра. Знайти площу бічної поверхні піраміди, якщо <A=120⁰ .

Розв’язок.

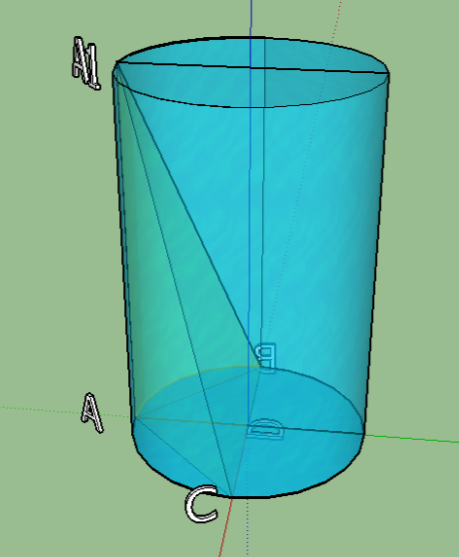
Проведемо AD _┴ BC та з’єднаємо точки A₁ і D відрізком A₁ D. Згідно теореми про три перпендикуляри, маємо A₁ D _┴ ВС. Так як дуга САВ містить 120⁰ , а дуги АС та АВ по 60⁰ , то BC= R, AB=R, з _∆ABD знаходимо AD= .

Застосуємо теорему Піфагора до трикутника AA₁D, отримаємо A₁D==. Отже S_∆A₁АВ= АВ▪АА₁= RH.

S_∆A₁BC=BC▪A₁D=.

 Кінцевий результат S_біч =2S_∆A1AB+S_∆A1BC=RH+R(4H+

 

Задача3.

 

Основою піраміди є правильний трикутник з стороною а. Одне з бокових ребр перпендикулярно до площини основи  і дорівнює b. Знайти радіус кулі, описаної навколо піраміди.

Розв’язок.

 

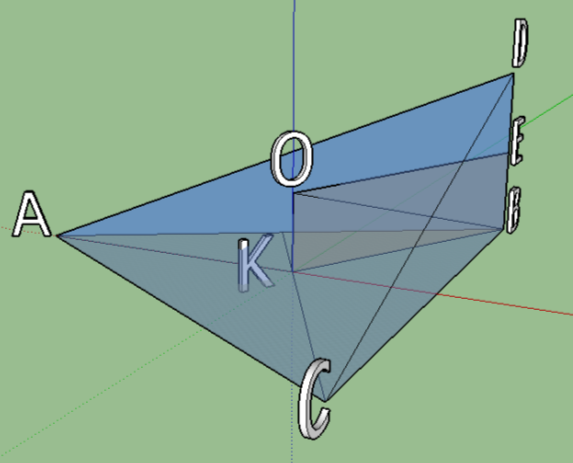
Нехай точка О – центр кулі, описаної навколо піраміди ABCD, тому OA=OB=OC=OD. Проведемо ОК _┴ площині АВС та ОЕ _┴ DB. Оскільки точка О рівновіддалена від вершин трикутника АВС, точка К є центром трикутника і ВК= . Далі, так як OB=OD, то ЕВ=ED= . За теоремою Піфагора з _∆ОКВ находимо ОВ= = =.         

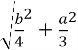IV. Домашнє завдання

Розв'язати задачу.

Знайти вагу піраміди Хеопса. Дані про розміри піраміди взяти з Вікіпедії .

 

V. Підбиття підсумків уроку

Запитання до класу

 

1. Скільки площин можна провести через пряму і точку, що їй не належить?

2. Діагоналі квадрата паралельні площині α. Як розташовані площина α і площина квадрата?

3. Яка з геометричних фігур не може бути паралельною проекцією паралелограма?