Розв’язування задач на знаходження невідомих елементів циліндра ( Опорний конспект. )

Опорний конспект. Тема: Розв’язування задач на знаходження невідомих елементів циліндра                                        

Прямим круговим циліндром називається тіло, утворене                                                                                                                                                                                                                                             обертанням   прямокутника навколо його сторони.                                                                         

Сторони ОА і О₁A₁  описують рівні круги, які лежать у  паралельних площинах і називаються основами циліндра.                                             

Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра.

Радіуси кругів називаються радіусами циліндра.

Відрізки бічної поверхні які паралельні і дорівнюють АВ називаються твірними циліндра.

Висотою циліндра називається відрізок, перпендикулярний до основ циліндра кінці якого належать основам. Висота циліндра дорівнює його твірній.

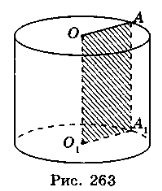
Осьовий переріз циліндра – прямокутник зі сторонами, що дорівнюють висоті циліндра і діаметру його основі

За рисунком укажіть вісь  циліндра:

а) OO₁  б) MN;  в) AB   г) OА.

За рисунком укажіть діаметр основи циліндра: 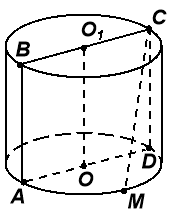                                              а) OO₁  б) CM  в) AD г) AB.

За рисунком укажіть відрізок, який дорівнює висоті циліндра:

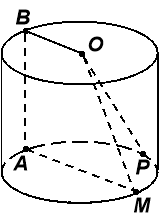а) OM  б) AM  в) AB  г) OP.

 За рисунком укажіть твірну циліндра:

а) MN  б) AB  в) AC  г) OO₁

Виконайте самостійно завдання:

1. Діагональ осьового перерізу циліндра дорівнює        см  і утворює кут 45⁰ з основою циліндра. Знайдіть радіус циліндра.

       Відповідь: 4 см

2. Радіус основи циліндра дорівнює 8 см, а діагональ осьового перерізу більша за твірну на 2 см. Знайти площу осьового перерізу циліндра.

       Відповідь: 1008 см².

3. Дві точки, які лежать на колах різних основ циліндра, з`єднані відрізком. Знайдіть його довжину, якщо радіус і висота циліндра відповідно дорівнюють 10см і 17см, а відстань від осі циліндра до відрізка – 4см

       Відповідь: 25 см

4. Діагональ осьового перерізу циліндра 10 см, радіус основи – 3 см. Знайдіть твірну.

Відповідь: 8 см.

Виконайте самостійно завдання:

5. Діагональ осьового перерізу циліндра дорівнює        см  і утворює кут 45⁰ з основою циліндра. Знайдіть радіус циліндра.

       Відповідь: 4 см

6. Радіус основи циліндра дорівнює 8 см, а діагональ осьового перерізу більша за твірну на 2 см. Знайти площу осьового перерізу циліндра.

       Відповідь: 1008 см².

7. Дві точки, які лежать на колах різних основ циліндра, з`єднані відрізком. Знайдіть його довжину, якщо радіус і висота циліндра відповідно дорівнюють 10см і 17см, а відстань від осі циліндра до відрізка – 4см

       Відповідь: 25 см

8. Діагональ осьового перерізу циліндра 10 см, радіус основи – 3 см. Знайдіть твірну.

Відповідь: 8 см.