Конспект уроку з алгебри для 7 - го класу на тему "Рівняння як математична модель задачі"

Рівняння як математична модель задачі

Мета: освітня: привчати учнів до поетапного самоконтролю і аналізу всіх елементів розв'язування задачі за допомогою складання рівнянь; фор­мувати вміння аналізувати здобуті корені рівняння відповідно до умови задачі; розвиваюча: розвивати логічне мислення, вміння аналізувати ситу­ацію; виховна: виховувати рішучість і упевненість під час прийняття рі­шень, інтерес до математики.

Тип уроку: засвоєння нових знань.

Обладнання: плакат з опорними схемами для розв’язування задач

 

                                                                                        Епіграф уроку:

                                                                        Розв'язування задач є найхарактернішим і специфічним різновидом вільного мислення.

В. Джеймс

                                                  ХІД УРОКУ

              І. Організація класу

II.Перевірка домашнього завдання

 Взаємоопитування. Працюючи в парах учні ставлять один одному запитання за домашнім завданням.

III .Актуалізація опорних знань

 Ще з курсу математики ви набули певного досвіду складати буквені вира­зи, які виражають різноманітні залежності між величинами. Оскільки на сьогоднішньому уроці ці вміння нам знадобляться, то зараз проведемо невели­ке тренування в переведенні залежностей між величинами на мову алгебри.

Усна робота:

Розв'яжіть задачу, склавши числовий вираз:

А)Купили 7 зошитів по 2грн. і 2 ручки по 4грн. Скільки грошей заплатили?

Б)Турист їхав 2год на поїзді зі швидкістю 60км / год і 3год йшов пішки зі швидкістю 5км / год. Яку відстань він подолав?

В)Розв'яжіть задачу, склавши буквений вираз:

- Купили 10 зошитів по Х грн. і 3 ручки по У грн. Скільки заплатили за всю покупку?

-Турист їхав 3год на автобусі зі швидкістю Х км / год і 2год йшов пішки зі швидкістю 4 км / год. Яку відстань він подолав?

Перейдіть від словесної моделі до математичної:

Числа В і С рівні

Число А на 18 більше числа В

Число Х в 6 раз менше числа У

IV. Мотивація навчальної діяльності

Дуже багато типових ситуацій з нашого побуту, наприклад звичайний похід у магазин, може обернутися необхідністю розв’язати деяку задачу. А значну кількість цих задач набагато легше розв’язати, склавши відповідне рівняння.

Повідомлення теми і мети уроку.

V. Сприймання й усвідомлення нового матеріалу

Ми навчилися розв'язувати лінійні рівняння з од­нією змінною для того, щоб застосовувати це вміння для розв'язування текстових задач. Як правило, задача являє собою деяку життєву ситуацію. Щоб розв'язати задачу, необхідно цю життєву ситуацію перекласти на мову алгебри — це називається скласти математичну модель задачі. Мате­матична модель — це опис якогось реального об'єкту або процесу мовою математичних понять, відношень, формул, рівнянь.

Для того, щоб скласти математичну модель задачі, потрібно спочатку вибрати основне невідоме, а потім, поетапно аналізуючи умову задачі, скласти відповідні рівняння. Само по собі рівняння, складене за умовою задачі, не є повною математичною моделлю реальної ситуації, відображеної в умові. Воно не враховує фізичних властивостей предметів і явищ, про які йдеться в задачі, реальних співвідношень між допустимими значеннями відповідних фізичних величин. Тому розв'язки рівняння можуть не відповідати дійсності, і треба обов'язково перевірити, чи задовольняють корені рівняння умову задачі, чи враховують змістові обмеження для зна­чень величин, що розглядаються. Отже, відповідь, яку дістали за складеним рівнянням, необхідно перевірити за змістом задачі. Чи задовольняє знайде­ний розв'язок саме умову, а не рівняння, складене за умовою задачі, адже можна неправильно скласти рівняння, а розв'язати його правильно.

Корисно з метою перевірки скласти й розв'язати задачу, в якій шукане число беруть за дане, а одне з даних - за шукане.

Приклад. Знайдіть, скільки треба квадратних плиток зі стороною 15 см, щоб застелити підлогу ванної кімнати, розміри якої 3,3м на 2,8м ?

Побудуємо математичну модель задачі: плитка має форму квадрата, підлога форму – прямокутника. Завдання, поставлене в задачі, мовою математики формулюється так: у скільки разів площа прямокутника зі сторонами 2,8м і 3,3м більша від площі квадрата зі стороною 15см?

Розв’язання математичної задачі:

1.                  площа прямокутника: 3,3 ∙ 2,8 = 9,24 (м²);
2.                  площа квадрата: 15² = 225 (см²) = 0,0225 (м²)
3.                 

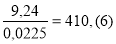
Відповідь: треба не менше ніж 411 плиток.

У формулюванні задачі використовуються не математичні поняття. Це прикладна задача.

VІ. Узагальнення і систематизація вивченого матеріалу

1. Робота біля дошки

1. Склади вираз для відповіді на запитання задачі:

1)  На скільки більше буде потрібно 2 – літрових банок, ніж 3 – літрових, щоб розлити в них х літрів компоту?

2) У дворі граються а хлопчиків і у 2 рази більше дівчаток. Для гри всі діти розбилися у команди по b дітей у кожній. Скільки вийшло команд?

2. Побудуй математичну модель задачі і розв’яжи її:

1) У залі 400 місць. Число рядів на 9 менше від числа місць у кожному ряді. Скільки рядів і скільки місць має кожний ряд?

2) Сторона квадратної шайби дорівнює 60 мм. Якої довжини повинен бути лист сталі, щоб з нього можна було зробити 52 шайби? Ширина листа 300мм.

2. Інтерактивна вправа «Дерево розв’язань»

Учитель пропонує учням задачу:

На светр, шапку і шарф витратили 555 г вовни, причому на шапку пішло у 5 раз менше вовни, ніж на светр, і на 5 г більше, ніж на шарф. Скільки вовни витратили на кожний виріб?

Клас розподіляється на три групи; першій дається вказівка при складанні рівняння взяти за основне невідоме кількість вовни, що пішла на светр, другій – кількість вовни, необхідної для шапки, а третій – для шарфа. Кожна група повинна шляхом обговорення прийти до єдиної думки під час складання рівняння і заповнити таблицю:

 

Светр	х	5х	5(х+5)
Шапка		х	х+5
Шарф		х – 5	х
Рівняння		5х + х + (х – 5)= 555	х+(х+5)+5(х+5)=555

 Кожна група пропонує своє розв’язання. Далі проводиться обговорення: яке ж невідоме доцільніше вибрати за основне? Шляхом голосування учні вибирають, що через х доцільно було позначити кількість вовни, що пішла на виготовлення шапки, оскільки при цьому дістають найпростіше рівняння. Учитель повинен підкреслити, що під час розв’язування задач на поділ числа на рівні частини в кратному відношенні для зручності беруть за основне невідоме найменшу величину(якщо це можливо).

 

VIІ.  Підбиття підсумків уроку

Учитель. Послухайте притчу.

Йшов мудрець, а назустріч йому три людини, які везли під палаючим сонцем візок з камінням для будівництва. Мудрець зупинив їх і поставив кожному запитання . У першого запитав: "Що ти робив цілий день?" Той з усмішкою відповів, що цілий день возив кляті камені. У другого запитав: "А що ти робив цілий день?" Той відповів: "Я сумлінно виконував свою роботу". А третій посміхнувся, його обличчя засвітилося радістю і задоволенням. "А я брав участь в будівництві храму". Нехай кожен сам оцінить свою роботу на уроці.

Хто працював як перша людина? 

Хто працював як друга людина?

Хто працював як третя людина? 

 

Я бажаю вам завжди працювати з радістю і задоволенням.

VІІІ. Домашнє завдання

Побудувати математичну модель задачі і розв’язати її.

Середній рівень

У 100 г гарбуза міститься 8мг вітаміну С. скільки треба взяти гарбуза, щоб дістати 100мг вітаміну С?

Достатній рівень

Комп’ютерний клуб планує працювати 9 годин на день і обслуговувати 38 членів клубу. Обслуговування кожного члена має відбуватися щоденно за окремим комп’ютером протягом 1,5 години. Яку найменшу кількість комп’ютерів потрібно клубові, щоб обслуговувати своїх клієнтів?

Високий рівень

В одній пачці 50 сірників, а у другій – 90. З першої пачки щодня використовують 7 сірників, а з другої – 12 сірників. Через скільки днів у другій пачці залишиться сірників удвічі більше, ніж у першій?