Розвиток процедурної компетентності на уроках математики

     Розвиток  процедурної  компетентності  на уроках  математики

Вчитель Карабут Валентина Володимирівна

Ряснянський НВК Краснопільської районної ради Сумської області

    Завдання сучасної освіти – це виховання відповідальної особистості, яка здатна до самоосвіти і саморозвитку, готова опрацьовувати різноманітну інформацію, аналізувати її, приймати виважені рішення, критично мислити, творчо розв’язувати проблеми, бути відповідальним за своє майбутнє.

    Математика як шкільний предмет має достатній потенціал для формування та розвитку тих якостей, які необхідні людині для того, щоб бути успішним в сучасному житті.

     Головне завдання учителя математики – розвивати математичні здібності і навички учнів, підвищувати престиж знань, формувати не тільки математичні, а й ключові компетентності, тобто формувати уміння використовувати набуті в процесі навчання знання в повсякденному житті.

    Для формування математичних компетентностей потрібні: здатність творчо мислити, послідовно міркувати та презентувати свої ідеї; уміти працювати в команді ( визначати пріоритети , планувати результати і нести відповідальність за їх реалізацію); ефективно застосовувати знання в реальному житті.

    Однією зі складових математичної компетентності є процедурна – уміння розв’язувати типові математичні задачі.

      Відомий науковець  Раков С. вважає, що

   процедурна компетентність –це уміння використовувати на практиці алгоритми розв’язування типових задач; відтворювати контекст задач, що виникають в індивідуальній та соціальній практиці та зводяться до типових; систематизувати типові задачі; уміти розпізнати типову задачу або зводити певну задачу до типової; використовувати різні інформаційні джерела для пошуку процедур розв’язання типових задач ( підручники, довідники, інтернет- ресурси). [4]

    Розглянемо зразки вправ, що формують процедурну компетентність в учнів 5 класу :

    Типовими є задачі на рух. Наприклад:

Задача

    Власна швидкість катера дорівнює 30 км/год, а швидкість течії річки- 1,4км/год. Знайдіть швидкість катера за течією і його швидкість проти течії річки [3,205].

Розв’язання.

1. 30 + 1,4 = 31,4 (км/год) – швидкість катера за течією.
2.  30 – 1,4= 28,6 (км/год) – швидкість катера проти течії.

Відповідь: 31,4 км/год, 28,6 км/год.

   Задача

    Власна швидкість моторного човна дорівнює 16,4км/год, швидкістьтечії річки – 1,8 км/год. Знайдіть швидкість човна за течією і його швидкість проти течії річки [ 3,207 ].

    Задача

     Швидкість човна проти течії річки дорівнює 18,8 км/год, а його власна швидкість – 20,2 км/год. Знайдіть швидкість течії  і швидкість човна за течією річки [3, 207].

  Типовими задачами є задачі на знаходження середнього арифметичного.

     Задача

     Автомобіль їхав 4 год зі швидкістю 54 км/год і 2 год зі швидкістю 60 км/год. Знайдіть середню швидкість автомобіля на всьому шляху[3,235].

Розв’язання.

1. 54 ∙ 4 = 216 (км) – проїхав зі швидкістю 54 км/год.
2. 60 ∙ 2 = 120 (км) – проїхав зі швидкістю 60 км/год.
3. 216 + 120 = 336 (км) – увесь шлях.
4. 4 +2 = 6 (год) – загальний час руху.
5.  336 : 6 = 56 (км/год) – середня швидкість руху.

Відповідь:  56 км/год.

Задача

    Автомобіль їхав 3 год зі швидкістю 56,4 км/год і 4 год зі швидкістю 62,7 км/год. Знайдіть середню швидкість автомобіля на всьому шляху [3,236].

          Задача

     Поїзд їхав 4 год зі швидкістю 64 км/год і 5 год зі швидкістю 53,2 км/год. Знайдіть середню швидкість поїзда протягом всього шляху [3,236].

           Задача

     Знайдіть середнє арифметичне чисел[3,236]:

1. 4,2 і 2,1;         2) 3,9; 6; 9,8 і 15,8.

    Задачі на відсотки є типовими і сприяють розвитку математичної компетентності учнів.

          Задача

    Полуниці містять у середньому 6% цукру. Скільки кілограмів цукру міститься у 15 кг полуниць?[3,239]

Розв’язання.

1. 15 : 100 = 0,15 ( кг ) – становить 1% маси всіх полуниць.
2. 0,15 ∙ 6 = 0,9 ( кг ) –цукру міститься у полуницях.

Відповідь: 0,9 кг.

Задача

     Сплав містить 8% міді. Скільки кілограмів міді міститься в 360 кг сплаву? [3,241].

          Задача

     Морська вода містить 6% солі. Скільки солі міститься в 250 кг морської води? [ 3,243].

     Зацікавленість учнів викликають задачі на відсотки із життєвим змістом :

         Задача

     Вкладник поклав у банк 4500 грн. під 9% річних. Яка сума буде у нього на рахунку через рік? [ 3,240 ].

Розв’язання.

Перший спосіб:

1. 4500 : 100 = 45 (грн.) – становить 1% вкладу.
2. 45 ∙ 9 = 405 ( грн.) – нараховано відсоткових грошей на кінець року.
3. 4500 + 405 =4905 ( грн. )  - стало на рахунку через рік.

  Другий спосіб:

1. 4500 : 100 = 45 ( грн. ) – становить 1%  вкладу.
2. 100 + 9 = 109 (% ) – початкової суми становили гроші на рахунку на кінець року.
3. 45 ∙ 109 = 4905 ( грн.) – стало на рахунку через рік.

Відповідь: 4905 грн.

   Провідне місце у шкільному курсі алгебри займають рівняння. Багато задач про просторові форми і кількісні співвідношення реального світу зводять до складання та розв’язування різних видів рівнянь.

    За типовими схемами розв’язують, наприклад, рівняння лінійні і квадратні, що вивчаються учнями середньої ланки.

    Розглянемо приклади.

Алгоритм розв’язування рівнянь, що зводяться до лінійних виду ax = b, де a і b – деякі числа, x – змінна.

1. Позбутися знаменників, якщо вони є.
2. Розкрити дужки.
3. Перенести доданки зі змінними в одну сторону рівняння, а без змінних- в іншу.
4. Звести подібні доданки.
5. Розв’язати отримане лінійне рівняння  ax = b за формулою  x = .

Розглянемо приклад:

( x – 3 ) = ( 2x + 3 ), [ 1,121 ].

1. Позбудемося знаменників (7 і 3) – обидві частини рівняння домножимо на число 21 – найменший спільний знаменник:   ∙ 21( x – 3 ) = ∙21(2x + 3);

6( x – 3 ) = 7(2x + 3).

2. Розкриємо дужки:  6x – 18 = 14x + 21.
3. Перенесемо доданок   6x у праву частину рівняння, а доданок 21 – у ліву, змінивши при цьому їх знаки:   -21 – 18 = 14x -6x.
4. Зведемо подібні доданки: -39 = 8x або 8x = -39.
5. Розв’яжемо отримане лінійне рівняння:  8x = -39;  x = -39 : 8;  x =- ;

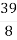x = -4.

Відповідь: -4 .

Алгоритм  розв’язування  квадратних  рівнянь виду ax ² +bx + c = 0, де x – змінна, a, b, c – деякі числа, причому a ≠ 0.

1. Обчислити дискримінант  D = b ² – 4ac.
2. Порівняти дискримінант з нулем і зробити висновок:  скільки розв’язків має квадратне рівняння.
3. Знайти розв’язки квадратного рівняння за формулою  .

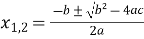Для квадратного рівняння  ax ² + 2kx + c=0, другий коефіцієнт якого є парне число, формулу розв’язків зручно записати так:  , де D₁ = k ² -4ac.

Теорема Вієта,     [ 2, 33 ]

ax ² + bx +c = 0,  a ≠ 0,  x ₁ ∙ x ₂ = ,  x₁ + x₂ = - .

У зведеному квадратному рівнянні  x ² + bx + c = 0 

x ₁ + x ₂ = -b;  x ₁ ∙ x _{2 =} c.

Розглянемо  приклад:   1) Розв’язати рівняння:   x ² +7x + 10 = 0,  [2, с.34 ]

D = 7 ² - 4∙1∙10 = 49 – 40 = 9,  D 0, отже рівняння має два різні розв’язки:

x ₁ = ;   x ₂ = ;       

Відповідь:  x ₁ = -2;   x ₂ = -5.

Дане рівняння можна розв’язати другим способом – за теоремою Вієта.

 x ₁ + x ₂ = -7;      x ₁ = -2;

 x₁ ∙ x ₂  = 10;        x ₂ = -5.

Можна запропонувати учням виконати наступні завдання.

Розв’язати рівняння

1. 3x ² = 0;     2) 3x ² – 4x + 1 = 0;     3) 5x ² – 4x -1 = 0;

6. 2x ² + 6x – 8 =0;     7) 4x ² – 4x – 3 = 0.

    Формування математичної компетентності на уроках відбувається через оволодіння учнями нових знань, умінь та навиків при вивченні математики.

    Оволодіння учнями процедурною компетентністю в системі забезпечує формування у них математичної компетентності як цілісного особистісного утворення.

Література:

1. Роєва Т.Г. Шкільна енциклопедія з алгебри. – Х. : Країна мрій ^ТМ ,2008. -464с.
2. Чекова А.М. Алгебра і початки аналізу в таблицях. 7 – 11класи. Навчальний посібник. Науково – методичний центр^ТМ , 2003. – 248с.
3. Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика: Підручник для 5-го класу. – Х.: Гімназія. 2005. – 288с.
4. Раков С. Формування математичної компетентності випускника школи як місія математичної освіти. Математика в школі.- 2007. №5- с.2-7.