Самостійна робота на тему: "Комбінації геометричних тіл"

Тема: Самостійна робота на тему: «Комбінації геометричних тіл»

1. Знайти площу поверхні (зовнішню та внутрішню) капелюха, розміри якого (в см) вказані на малюнку.

Розв’язання.

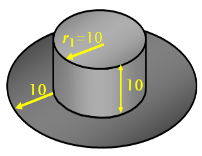Якщо дно капелюха опустити на площину його полів, то отримаємо коло з радіусом

Площа цього кола

Знайдемо площу бічної поверхні циліндричної частини

Знайдемо площу капелюха

= 2 ( + ) = 2 (400 + 200) = 1600 ).

Відповідь: S = 1600 .

2. Основа конуса збігається з нижньою основою циліндра, вершина конуса – центр верхньої основи циліндра. Осі, висоти, радіуси циліндра і конуса збігаються.

Знайти висоту описаного навколо конуса циліндра, якщо твірна конуса нахилена до площини основи під кутом 30 і дорівнює 8 см.

Розв’язання.

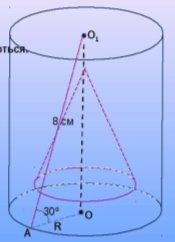                  В прямокутному трикутнику АО: кут АО дорівнює 30, як кут між похилою та площиною основи. Катет, який лежить проти кута в 30 вдвічі менше гіпотенузи. Тому висота циліндра дорівнює

8 : 2 = 4 (см).

Відповідь: 4 см.

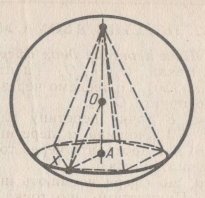
3.Доведіть, що центр кулі, описаної навколо правильної піраміди, лежить на її осі.

Розв’язання.

Опустимо перпендикуляр ОА з центра кулі О на площину основи піраміди. Нехай Х – довільна вершина основи піраміди. За теоремою Піфагора

= - = - .

Таким чином, АХ одне і те саме для будь-якої вершини основи піраміди. А це означає, що точка А є центром кола, описаного навколо основи піраміди. Отже, центр кулі О лежить на осі піраміди.