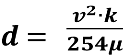«ЩО НАВКОЛО БАЧУ, ПРО ТО Й СКЛАДУ ЗАДАЧУ» КОМПЕТЕНТНІСНО ОРІЄНТОВАНІ ЗАДАЧІ ПІД КЛЮЧ (методичний супровід набуття студентами предметних математичних компетентностей)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

 

ВІДОКРЕМЛЕНИЙ СТРУКТУРНИЙ ПІДРОЗДІЛ

«ХАРКІВСЬКИЙ ФАХОВИЙ КОЛЕДЖ ХАРЧОВОЇ ПРОМИСЛОВОСТІ ДЕРЖАВНОГО БІОТЕХНОЛОГІЧНОГО УНІВЕРСИТЕТУ»

 

 

 

 

 

 

 

«ЩО НАВКОЛО БАЧУ, ПРО ТО Й СКЛАДУ ЗАДАЧУ»

КОМПЕТЕНТНІСНО ОРІЄНТОВАНІ ЗАДАЧІ ПІД КЛЮЧ

(методичний супровід набуття студентами предметних  математичних компетентностей)

 

 

 

 

 

 

 

        КОНКУРС “Педагогічний ОСКАР-2025”

                                                     НОМІНАЦІЯ “ інноваційна діяльність                  

        методичного (педагогічного) кабінету та

        предметних (циклових) комісій, викладачів ”

        (досвід роботи викладача)

        ЦИКЛ  природничо-математичних дисциплін

 

 

 

 

 

 

 

 

 

2024

Укладач: Чиновата Зоя Анатоліївна, викладач математики, спеціаліст вищої кваліфікаційної категорії, викладач-методист

 

 

 

 

 

 

В роботі розглянуто актуальність компетентнісного підходу до вивчення математики, технології створення компетентнісно орієнтованих задач, педагогічні методики навчання студентів розв’язанню таких задач, вмінню складати математичні моделі життєвих ситуацій та розробляти стратегії їх розв’язування, аналізувати та інтерпретувати отримані в процесі розв’язання результати. Робота містить авторський збірник компетентнісно орієнтованих задач.

          Для викладачів та студентів ВНЗ І-ІІ  рівнів акредитації, слухачів підготовчих курсів, учнів ЗЗСО, абітурієнтів.

 

 

 

 

 

 

 

 

 

 

Рекомендовано цикловою комісією природничо-математичних дисциплін.

Протокол №____________ від “_____”_______________2024 р.

 

 

 

 

 

 

 

 

 

«ЩО НАВКОЛО БАЧУ, ПРО ТО Й СКЛАДУ ЗАДАЧУ»

КОМПЕТЕНТНІСНО ОРІЄНТОВАНІ ЗАДАЧІ ПІД КЛЮЧ

(методичний супровід набуття студентами предметних  математичних компетентностей)

 

«Просто зроби це!»

слоган компанії Nike

 

ВСТУП

Концепція впровадження в навчання компетентнісно орієнтованих завдань втілюється в систему української освіти вже більше 10 років. В шкільній освіті ця реформа має назву Нова Українська Школа (НУШ). У 2024-2025 навчальному році НУШ переходить до класів базової загальної середньої освіти (7-9 класи). За три роки реформа буде впроваджуватися і в систему повної загальної середньої освіти (10-12 класи) та, відповідно, до системи професійно-технічної освіти. Тому зараз вже потрібно вибудовувати систему завдань, які сформують в студентів ключові компетентності, предметні математичні компетентності на рівні, достатньому для забезпечення їх життєвих потреб та професіональної діяльності.

Особистісно зорієнтований підхід до навчання та проблемну діяльність, що впроваджують сьогодні в освітні заклади, було започатковано ще в часи Аристотеля, Сократа, Платона, Евкліда, Піфагора. Сократ вважав, що вчитель має допомагати учню у пошуках істини, а кожен з учасників діалогу (вчитель і учень) мають бути рівними. Ефективність спільної діяльності вчителя та учня на основі життєвих ситуацій описано в праці «Мистецтво розв’язувати задачі» давньогрецького математика Паппа Олександрійського (ІІІ-ІV ст.), де показано прийоми, які необхідно застосовувати, коли задачу неможливо розв’язати за допомогою логічних способів. І сьогодні є актуальними і задача Діофанта, викарбувана на його надгробку, і задача індуського математика ХІІ століття Бхаскари про квіти лотосу. Франсуа Рабле і Мішель Монтень ( XV – XVI ст.) відстоювали необхідність освоєння дітьми реальних і корисних знань, а не «порожніх слів». «Арифметика»  Леонтія Магницького (VІІІ ст.) сала першим на той час прикладним підручником із задачами про купців та мореплавців. Цінним джерелом стала праця, що стосується основних ідей гуманістичної педагогіки А. Маслоу (ХХ ст.).

Таким чином, протягом всієї  освітянської історії математика завжди наближалася до життя і намагалася допомагати розв’язувати життєві задачі. Іноді, навіть, виникає питання: хто ж вона - цариця всіх наук чи слуга?

В кінці ХХ століття світ стрімко починає змінюватися, у суспільства з’являються нові запити, оскільки з’являються нові професії, галузі науки, технології, обладнання, цифрові інструменти. І знову освіта повинна обслуговувати сучасні запити. Для цього як раз і необхідна нова система компетентнісно  орієнтованого навчання. Теоретично – нічого нового. Математика завжди обслуговувала потреби суспільства. Практично - змінилося само суспільство, тому і відбуваються концептуальні зміни в сучасній освіті з орієнтиром на набуття студентами ключових і предметних компетентностей.

В посібнику розглянуто теоретичні аспекти компетентнісно орієнтованого навчання, методику складання компетентнісно орієнтованих задач, педагогічні практики застосування таких задач на заняттях із студентами з власного досвіду. Робота містить авторські компетентнісно орієнтовані задачі, які можна використовувати на заняттях зі студентами, на заняттях підготовчих курсів, для підготовки до Національного Мультипредметного Тесту або Зовнішнього Незалежного Оцінювання. Частина задач систематизована за наскрізними лініями компетентностей, розглянуто задачі від креативного математика Юрія Захарійченка, викладача вищої математики в Києво-Могилянській академії, що завжди проводить уроки математики «зі спецефектами».

Для викладачів математики коледжів, професійних ліцеїв, шкільних вчителів математики, студентів педагогічних вишів, допитливої молоді, яка цікавиться математикою.

    

ОСНОВНА ЧАСТИНА

Актуальність компетентнісно орієнтованого навчання

Компетентнісно орієнтований підхід - один із нових концептуальних орієнтирів, напрямів розвитку змісту освіти в Україні та розвинених країнах світу. Відомі міжнародні організації, що нині працюють у сфері освіти, останніми десятиліттями вивчають проблеми, пов'язані з появою компетентнісно зорієнтованої освіти.

Відповідно до Закону України «Про освіту» «Компетентність – це динамічна комбінація знань, умінь, навичок, способів мислення, поглядів, цінностей, інших особистих якостей, що визначає здатність особи успішно соціалізуватися, провадити професійну та/або подальшу навчальну та діяльність».

За тим самим законом, компетентність вимірює здатність та готовність діяти, залежно від поставлених проблем. Це прихована характеристика особистості, й дізнатися про її сформованість непросто. Для цього потрібні особливі завдання, які називаються компетентнісно орієнтованими. Такі задання відрізняються від інших наступними критеріями:

• більший обсяг тексу  в основі завдання;
• багато ілюстративного матеріалу: схеми, діаграми, інфографіка, світлини, рисунки;
• більша дотичність до повсякденного життя;
• недостатність лише певних знань для правильної відповіді на завдання.

Компетентнісно орієнтовані завдання перевіряють рівень сформованості компетентності – ефективного використання знань в життєвих ситуаціях. Розв’язування таких завдань є тестуванням не досягнень студентів, а їх можливостей розв’язати ту чи іншу проблему. Такі завдання вимагають аналізу матеріалу, виокремлення ключових думок, порівняння, читання графіків та діаграм, розуміння логічних зв’язків між явищами і процесами (рис. 1).

рисунок 1. Квітка компетентностей

 Якщо розв’язання є груповим, то оцінюється добір аргументів і фактів на користь власної думки щодо розв’язання задачі та вміння спростувати думку опонента. Компетентнісно орієнтовані завдання дозволяють розглянути різні точки зору на проблему для отримання більш повної інформації. Вони розвивають критичне мислення, вміння вибудовувати та перевіряти аргументи, робити свідомий вибір і обґрунтовувати його, і в решті решт знаходити через взаємодію та співпрацю оптимальне вирішення проблеми. З погляду на те, що колективне розв’язання компетентнісно орієнтованих задач формує навички роботи з інформацією, можна стверджувати, що такі завдання навчають студентів протидіяти небажаному впливу недостовірної інформації та тренують їх «інтелектуальну мужність».

Історя розвитку компетентнісної математики

В нвчанні математиці завжди був компетентнісний підхід. Вона завжди обслуговувала практичні портеби суспільства. Афоризм «Математика – цариця всіх наук» може бути ділемою. Чи цариця вона, чи слуга? Адже вона завжди йшла в тандемі з усіма іншими науками.

Математика як наука зароджувалася ще в давній Греціїї з огляду на практичні потреби. Геометрія – наука про геметричні фігури - з'явилася у зв'язку з необхідністю вимірювати площі земельних ділянок. В епоху Середньовіччя розвивається мореплавство, з'являється необхідність астрономічних вимірювань і розрахунків – так виникає тригонометрія. в середньовічну математику спробував механізувати арифметичні розрахунки Раймон Луллій, оригінальний європейський мислитель-інтелектуал, який вигадав «логічну машину» у вигляді рухомих паперових кругів, що накладалися один на одний. Проте розвиток ремісництва та інженерної думки на той час не дозволяв сконструювати таку машину.

Новий час вибухнув стрімким розвитком машин і механізмів. Математика обслуговує інтереси промисловості: суміші, пропорції, креслення деталей, розробки корисних копалин, щахти, кількісний аналіз промислових процесів. Потім епоха Новітньої історії додає математичним задачам торгівельного присмаку: відсотки, ціноутворення, складські приміщення, перевезення товарів, плата найманої праці, амортизація, капітал, банківські операції тощо. Паралельно з прикладною математикою розвиваються природничі науки, що базуються на складних розрахунках математичного аналізу, диференціального та інтегрального числення.

Таким чином, матетматика в усі часи допомагала розв'язувати прикладні життєві задачі. І компетентнісно-орієнтоване навчаннє – це не щось нове, а добре забуте старе. Суспільство змінювалося, і відповідно до його запитів змінювався зміст освіти - з'являлися нові освтіні технології, методи навчання, цифрові інструменти, змінювалося освітнє середовище (рис.2,3). Проте парадигма освіти – залишається сталою – дати знання і навчити застосовувати їх на практиці.

рисунок 2. Сюжети компетентнісно-орієнтованих задач до часів НУШ

рисунок 3. Сюжети компетентнісно-орієнтованих задач часів НУШ

Наприклад, ось так виглядає, сюжет однієї і тої самої задачі в підручниках з різницею в 26 років:

• При обстеженні горизонтальних печер Оптимістичної та Озерної в Західній Україні спортсмени пройшли під землею 210 км 320 м. З'ясувалося, що печера Оптимістична на 8 км 320 м довша за Озерну. Знайти довжину кожної печери. (В.К. Совайленко «Система обучения математике в 5-6 классах». 1991 рік).
• Однією з найбільш унікальних природних пам'яток України є найдовша перчера в Євразії – Оптимістична в Тернопільській області. Довжина її ходів 250 км. Порахуйте, за скільки днів зможе обійти всі ходи печери експедитор, якщо рухатиметсься зі щвидкістю 2 км/год і щодня буде перебувати в русі впродовж 8 годин. (Д.В. Васильєва, Н.І. Василюк «Збірник задач з математики. 5-9 класи. Наскрізні лінії компетентностей та їх реалізація. 2017 рік.)

Компетентнісно орієнтовані завдання в системі  STEM освіти

В математичній галузі, однією з цілей якої є  розуміння студентами можливостей застосування математики в особистому та суспільному житті, компетентнісно орієнтовані завдання є основою STEM освіти. Концепція STEM освіти втілює широкий міждисциплінарний підхід до навчання, який інтегрує чотири галузі знань з метою набуття студентами життєвого досвіду:

• наука (Science);
• технології (Technologies);
• інженерія (Engineering);
• математика (Mathematics).

STEM освіта формує важливі навички в кожній галузі, а саме:

• наукові: спостереження, експеримент, припущення, проблемні питання;
• технологічні: інструментарій, динамічні моделі, комп’ютерні та цифрові пристрої;
• інженерні: вирішення проблем, моделювання та конструювання за зразком або за власним задумом;
• математичні: проектування, алгоритми, дослідження геометричних фігур, обчислювальні навички визначення форм, об’ємів, розмірів предметів.

STEM освіта також формує і такі важливі в ХХІ столітті м’які навички, як самонавчання, інноваційність, співпраця, творчість, підприємливість. Для ефективної реалізації концепції STEM освіти потрібно розвивати партнерство із роботодавцями та науковцями, залучати бізнес та наукові установи до розвитку природничо-математичної освіти.

Компетентнісно орієнтовані задачі формують в студентів STEM-компетентність – розвиток здатності інтерактивно активізовувати та етично використовувати знання, навички, цінності, ставлення та технології з метою досягнення індивідуального, колективного та глобального добробуту. Оцінити STEM-компетентність студента/студентки -  означає оцінити його/її вміння досліджувати, проєктувати, конструювати, обчислювати, пізнавати. Це нагальна потреба часу, це нові запити суспільства, це нові виклики освіти ХХІ століття.

Під час виконання компетентнісно орієнтованих завдань оцінюється:

• співпраця;
• комунікація;
• креативність;
• аналіз даних;
• дослідження проблеми;
• лідерські вміння;
• проєктування з урахуванням принципу природовідповідності;
• організаційні вміння;
• вирішення проблеми;
• використання технологій.

Ефективність реалізації STEM-освіти визначається здатністю учнів інтегрувати знання та вміння з різних STEM-дисциплін, а також пов’язувати їх із реальними життєвими проблемами.

Методика створення компетентнісно орієнтованих задач

Отже, коли освітній процес має за мету сформувати компетентності в студентства, викладачам необхідно діагностувати не рівень знань чи навіть умінь, а саме рівень сформованості тієї чи іншої ключової або предметної компетентності. Оцінювання таких завдань передбачає інший підхід. Якщо, наприклад, перевірочна робота на занятті чи тест ЗНО насамперед спрямовані на визначення того, чи добре здобувач освіти засвоїв навчальний матеріал та чи може його застосувати для розв’язування типових завдань, то гра та дослідження орієнтовані на перевірку рівня сформованості компетентностей — здатності ефективно використовувати набуті знання, уміння й навички, власний досвід на практиці, в різних життєвих ситуаціях. В розрізі цього компетентнісно орієнтовані завдання мають іншу структуру.

Компетентнісно орієнтовані завдання мають властиву для них конструкцію, тобто повинні містити такі складові:

• мотивацію (стимул), що підводить до проблеми, зацікавлює та мотивує до  розв’язання;
• інформацію — набір відомостей, які потрібні або можуть стати у нагоді в процесі  пошуку правильної відповіді. При цьому часто як у стимулі, так і в інформації можуть міститися надлишкові відомості, не потрібні для розв’язування, хоча у  деяких завданнях ці компоненти неможливо розділити;
• сформульоване запитання/проблему — власне завдання, пояснення того, що  необхідно зробити;
• критерії оцінювання відповіді — набір характеристик, що визначають правильність, доцільність і відповідність отриманого результату поставленому завданню.

Особливістю компетентнісно орієнтованих завдань є те, що вони взагалі можуть не вимагати наявності певних знань, а наводити їх у блоці інформації. Водночас такі завдання навпаки можуть призводити до отримання учнем/ученицею нових відомостей чи навичок. Зрештою, бувають і компетентнісно орієнтовані завдання, які потребують значного обсягу знань і вмінь для розв'язання. Отже, «знаннєва потреба» завдання не може слугувати надійним критерієм для визначення того, чи є це завдання компетентнісно орієнтованим. Однак практичне, життєве спрямування такого завдання сприяє зменшенню обсягу введених у завдання знань.

Іншою визначальною рисою компетентнісно орієнтованих завдань є їхня когнітивна складність. Зазвичай такі завдання потребують уміння виокремлювати в тексті головні думки, аналізувати тексти та зображення до них, порівнювати, «читати» графіки та діаграми, розуміти логічні зв’язки між явищами та процесами тощо. Однак навички, яких вимагає розв’язання такого завдання, є життєво необхідними, на відміну від знання певних фактів чи наявності певних предметних умінь, навчити яким так прагне наша освітня система.

Освітні науковці та фахівці працюють сьогодні над створенням модельних навчальних програм та підручників, в яких пропонують обов’язковими компетентнісні блоки із задачами. Але, за словами Ніни Тарасенкової, завідувачки кафедри математики та методики навчання математики Черкаського національного університету імені Богдана Хмельницького, авторки підручників і посібників методичного супроводу математики в НУШ, в підручниках таких завдань не може бути, оскільки в підручниках заборонено містити некоректні задачі. А компетентнісно орієнтовані задачі – це майже всі некоректні задачі! Бо це суто життєві задачі! В них може бути як і надлишок, так і недостача даних, кілька правильних відповідей, декілька способів розв’язання, ілюстративний матеріал, що не знадобиться або частково знадобиться для розв’язання. В навчальних підручниках за правилами підручникотворення таких задач не повинно бути.

Суть компетентнісно орієнтованих задач полягає в тому, щоб звичайний життєвий сюжет перекласти на математичну мову, тобто створити математичну модель задачі. Але життєві ситуації не завжди можна підпорядкувати чітким математичним конструкціям. Наприклад, коли ми розглядаємо задачі на рух, то за траєкторію руху приймаємо пряму, швидкість руху вважаємо сталою, опором повітря нехтуємо тощо. Насправді в реальному русі так практично не буває ніколи. Проте, якщо всі ці фактори враховувати, то математичну модель неможливо буде скласти, або вона буде надскладною, і студент/ка не зможе її розв’язати. Ці задачі розглядаються в спеціальних математичних курсах прикладної математики. В такому випадку задачу потрібно адаптувати до існуючих математичних понять, законів, правил. Такі задачі називають рафінованими сюжетними задачами. В них описується життєва ситуація із мінімальним набором вхідних даних – рівно стільки, скільки потрібно для розв’язання. В підручниках це типові задачі на рух, на сумісну роботу, на знаходження найбільшого та найменшого значення функції, обчислення площ і об’ємів предметів геометричної форми. Основна мета таких задач – набуття студентами предметної математичної компетенції математизувати сюжет від умови до математичної моделі.

В повсякденному житті немає типових задач, так само і немає певних чітких алгоритмів розв’язання, як в підручнику. Інколи немає навіть часу, аби подумати над розв’язанням. Наприклад, якщо ви переходите дорогу, то ви думаєте, встигну чи не встигну перейти на зелене світло, зупиниться чи не зупиниться машина переді мною тощо.  Таким чином, фактично в житті не існує задач в прямому сенсі – є проблема, яку потрібно вирішити. Яким шляхом студент/студентка це зробить  - і є його/її досягненням, які ми оцінюємо. Тільки аналізуючи, як студент/студентка поводить себе в тій чи іншій ситуації, можливо оцінити рівень сформованості його/її компетентностей.

Етапи розв’язання компетентнісно орієнтованої задачі:

• аналізування умови задачі;
• створення математичної моделі задачі;
• вибір стратегії розв’язання математичної моделі задачі;
• складання плану розв’язання математичної моделі задачі;
• розв’язання математичної моделі;
• отримання відповіді до математичної моделі;
• інтерпретація відповіді до математичної моделі;
• отримання відповіді до задачі.

Розглянемо приклади компетентнісно орієнтованих задач та проаналізуємо їх складові.

Економимо воду

Якщо з крану тече цівка холодної води товщиною у сірник, то лише за добу у такий спосіб втрачається 70 відер води. О 8-й годині ранку  Катруся погано закрила водопровідний кран, і вода цівкою товщиною у сірник текла доти, поки вона 0 14-й годині не повернулася додому. Визначте, скільки літрів води витекло і скільки грошей це буде коштувати родинному бюджетові Катрусі. (Самостійно дізнайтеся про тарифи на воду). Пам’ятайте! Одна крапля води з крана за 1 с перетворюється на рік на 3 т марно витраченої води!

Розглянемо складові  задачі:

• мотивація: даремно витрачена вода – даремно витрачені кошти;
• інформація: кількість дарма вилитої води за певний час; задача містить надлишкову інформацію про краплю води, яка за рік перетворюється на 3 тони. Вона не використовується для розв’язання, проте є важливою складовою як для мотиваційного, так і для інформаційного блоку. Є в задачі також і нестача інформації – про тарифи на воду пропонується дізнатися самостійно;
• сформульоване запитання: скільки літрів води витекло і скільки грошей це буде коштувати родинному бюджетові Катрусі;
• критерії оцінювання: в даному випадку це просто відповідь до задачі, можуть також бути і тестові варіанти відповідей, які допоможуть не тільки обчислювальним, а й логічним шляхом обрати відповідь.

Пам’ятник Флемінгу

Першовідкривачеві пеніциліну бактеріологу й лікарю Александеру Флемінгу 1964 року в Мадриді поруч з ареною «Лас-Вентас» встановлений пам’ятник. Закінчіть напис, який можна прочитати на постаменті: «Доктору Флемінгу від вдячних …»

1.      тореадорів;
2.     військових;
3.      артистів;
4.     пацієнтів;
5.      футболістів.

 

       

рисунок 4. Пам'ятник Алексанлеру Флемінгу

В цій задачі всі складові, і мотиваційна, і інформаційна, і питальна, і навіть оцінювальна злилися разом. Вона цікава тим, що це задача не на розв’язання, а на вирішення проблеми, на вміння показати рівень сформованості компетентності. Правильна відповідь а) тореадорів. Обрати стратегію розв’язання можна декількома шляхами. По-перше, розглянути ближче пам’ятник (рис. 4), як на світлині ліворуч, – на ньому написано слово тореадор. Але в умові задачі наводиться інший варіант пам’ятника, як на світлині праворуч, де надпису не видно. Для цього потрібно переглянути в інтернеті певний матеріал. По-друге, можна так само в інтернеті знайти інформацію про Александера Флемінга та арену «Лас-Вентас». Флемінг винайшов пеніцилін, а арена «Лас-Вентас» - це найбільша в Іспанії арена для кориди – бою биків. Вочевидь, пеніцилін рятував тореадорів від інфекцій, що потрапляли в їх організм при травмуванні рогами биків.

Компетентнісно орієнтовані завдання в освітньому процесі є:

• способом перевірки рівня сформованості ключових та предметних компетентностей;
• мотивацією для вивчення певного матеріалу, теми;
• захопливою вправою для групової роботи, яка сприятиме не тільки вивченню нового, а й закріпленню вже відомого.

Реалізація наскрізних ліній ключових компетентностей

Наскрізні лінії — це соціально значимі надпредметні теми, що сприяють формуванню в учнів уявлення про суспільство в цілому — розвивають здатність застосовувати отримані знання у різних ситуаціях; засіб інтеграції ключових і загальнопредметних компетентностей — навчальних предметів та предметних циклів. Вони відповідають виклику сучасності, урівноважують знаннєвий і компетентісний компоненти змісту освіти, є інструментом для використання інноваційних методик навчання, функціональним документом для студентів і викладачів у пошуку відповіді на питання «Для чого це потрібно вивчати?».

Впровадження наскрізних змістових ліній на заняттях з математики передбачає актуалізацію набутих під час вивчення інших предметів знань, умінь і способів діяльності для розв’язування практичних завдань, розвиток умінь здійснювати інформаційний пошук, знаходити і перетворювати необхідну інформацію, використовувати додаткову літературу. Необхідність інтеграції змістових ліній не тягне за собою якихось радикальних змін у навчальному процесі, а передбачає лише зміщення акцентів на більш прикладні аспекти теми.

Держстандарт освіти розглядає чотири наскрізні лінії ключових компетентностей:

• «Екологічна безпека та сталий розвиток»;
• «Громадянська відповідальність»;
• «Здоров'я і безпека»;
• «Підприємливість і фінансова грамотність».

Для наскрізної лінії «Екологічна безпека та сталий розвиток» характерні ідеї про те, що екологію погіршують люди, тож і впливати, сприяючи формуванню екологічних цінностей, потрібно саме не громадян. Розв’язання задач екологічного змісту формує екологічну грамотність, відповідальність за довкілля, дбайливе ставлення до навколишнього середовища. Змістом таких задач може кількісний аналіз забруднень води, повітря, ґрунтів, статистичні дані з відкритих джерел про зміни популяцій тварин, про флору та фауну Червоної Книги України, порівняльний аналіз викидів різних видів транспорту, про переробку та сортування сміття, альтернативні джерела енергії тощо.

Наприклад. На рисунку 5 подано інфографіку із містами України із найбільш забрудненим повітрям. Проаналізуйте інформацію, визначте найбільш та найменш забруднені міста. У скільки разів відрізняється найбільша та найменша забрудненість. Скільки відсотків становить індекс забрудненості у Львові від індексу забрудненості в Дніпрі? Складіть таблицю відповідностей забруднень в містах у порядку зростання. Відповідно до таблиці побудуйте стовпчасту діаграму рівнів забрудненості у порядку зростання. Побудуйте кругову діаграму хімічного складу забруднень у місті Кам’янське.

 

рисунок 5. Міста України з найбільш забрудненим повітрям

Для наскрізної лінії «Громадянська відповідальність» характерні наступні складові:

• громадянська самоідентификація;
• свідоме і добровільне дотримання законів;
• сформована система національних цінностей;
• уміння передбачати наслідки своїх дій і вчинків;
• усвідомлення власної відповідальності за оточуючий світ;
• повага до державної символіки, історії, культури;
• вмотивованість до суспільно значимих дій і вчинків;
• вибір професії за здібностями;
• усвідомлена потреба в засвоєнні системи знань;
• толерантне ставлення до інших людей;
• здатність відстояти свої погляди;
• активна участь у громадській діяльності.

Відповідальний громадянин – це той, хто ідентифікує себе громадянином держави, у якій живе, навчається, працює, поважає громадянські демократичні цінності, виконує громадські обов’язки, будує власну траєкторію інтелектуального, фізичного, професійного розвитку, дбає про розвиток країни.

Сюжетами компетентнісно орієнтованих задач з формування громадянської відповідальності можуть бути площі та населення областей України, визначні історичні та культурні пам’ятки України, літак «Мрія», благодійна допомога, волонтерство, засмічення ґрунту та водойм, маршрут на Гугл картах, альтернативні джерела енергії, телефонна «гаряча лінія», допомога по безробіттю, місцеві вибори, спортивні досягнення тощо.

Наприклад. Розгляньте графіки кількості сиріт в Україні, всиновлених іноземцями та українцями потягом 6 років з 2014 до 2020 року (рис.6). Чи збігаються області визначення та області значень функцій на графіках? На яких проміжках графік кожної функції зростає та спадає?

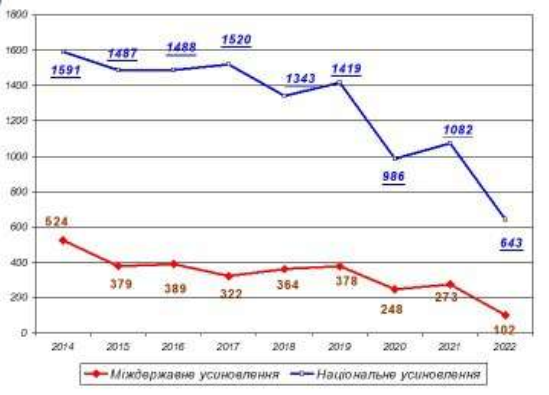
рисунок 6. Усиновлення дітей-сиріт та позбавлених батьківського піклування

«Здоров'язбережувальна компетентність» передбачає дбайливе відповідальне ставлення до свого власного фізичного, психічного, ментального, соціального і духовного здоров'я та здоров'я свого оточення. Ця компетентність передбачає:

• раціональне харчування, повноцінний сон, рухова активність, здоровий спосіб життя, дотримання санітарно-гігієнічних норм праці та відпочинку;
• безконфліктне спілкування, співпраця, відстоювання власної точки зору, співчуття, поведінка в стресових ситуаціях;
• відповіальність за прийняті рішення, самооцінка та самоконтроль, визначення і досягнення життєвих цілей, мотивація успіху та тренування волі, інтелектуальної мужності.

Нобхідність збереження здоров'я людини і запобігання його руйнації – важлива проблема сьогодення. Заклади освіти та сім'я – найефективніші інституції формування здорового способу життя і культури здоров'я дітей та миолоді. Здорова людина – це здорова нація. А здорова нація – це показник цивілізованості держави та головний чинник її безпеки.

Наприклад. Проаналізуйте схему евакуації студентів коледжу у разі виникнення пожежі (рис.7). Скільки існує варіантів виходу з приміщення, якшо не відкриті запасні виходи? Якщо відкриті запасні виходи? Скільки варіантів виходу існує в студентів, що знаходяться в кабінеті № 4 (пам'ятайте, що у разі пожежі краще вибирати найближчі до вас виходи)? Проаналізуйте аналогічну схему у вашому навчальному закладі. Скільки у вас є варіантів для того, щоб залишити будівлю у випадку надзвичайної ситуації?

 

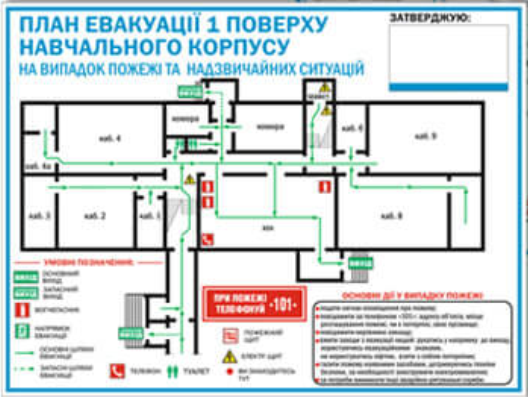
рисунок 7. План евакуації з навчального корпусу на випадок пожежі

Що навколо бачу, про те й складу задачу

Компетентнісно орієнтовані задачі є скрізь навколо нас! Для їх укладання можна використовувати будь які сюжети, навіть тексти із підручника за умови, що вони будуть містити зв’язані тексти, а не набір абстрактних речень.

Піца? Піца. Піца!

Про піцу можна скласти безліч задач, не боячись, шо задача може бути некоректною (рис.8). Умову складаєте самі, на свій розсуд, а питання до задачі можна поставити такі:

 

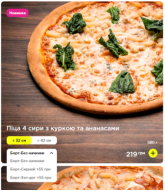
 рисунок 8. Про піцу можна скласти безліч задач!

• Якої форми може бути піца?
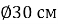
• Що означають цифри 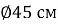в меню?
• Як поміряти діаметр піци?
• Як знайти довжину бортика піци?
• Як знайти площу піци?
• Яку геометричну форму має шматочок піци?
• Як обчислити площу шматка піци?
• Як дізнатися, на скільки шматків порізали піцу?
• Який кут між прямими (бічними) сторонами шматочка піци?
• Розрахувати калорійність піци за інформацією в меню.
• Якої форми буде метрова піца?
• Що вигідніше взяти одну 45-ти см піцу чи дві по 30 см?
• Якої форми і якого розміру має бути коробка для піци?
• Експериментальним шляхом знайти число пі.
• Експериментальним шляхом знайти залежність між центральним кутом, що обмежує шматок піци, і площею шматка піци.

 

Проєкт «Об'єм соку»

рисунок 9. Проєкт «Об'єм соку»

ОБ’ЄМ СОКУ

студентський економіко-математичний дослідницький проект

ПАСПОРТ ПРОЕКТУ

Актуальність проекту: споживачам сьогодні виробники та торгівельні мережі пропонують величезний асортимент товарів. Не маючи певних знань та не володіючи елементарними навичками споживчої поведінки,  дуже часто покупці купують зовсім не той товар, який їм необхідний, або переплачують за зайвий обєм, масу, тару й тому подібні непотрібні речі.

Цілі проекту та очікувані результати:

•    навчитися застосувати теоретичні знання про об’єми многогранників на практиці;
•    експериментальним шляхом визначити об’єми споживчих товарів - пакетів із соком;
•    дослідити відповідність заявленої інформації виробника про товар дійсності;
•    дослідити вплив закону спадної граничної корисності на цінову політику виробників та торгівельних мереж і  на споживчу поведінку покупців;
•    вдосконалити вміння презентувати себе та результати своєї роботи;
•    розвинути здатність студентів до самоосвіти та самовдосконалення, вміння підвищити свою свідомість та самооцінку;
•    сформувати почуття відповідальності за виконання своєї роботи та роботи команди і всього проекту в цілому;
•    розвинути здатність логічно обґрунтовувати власну позицію та приймати виважені рішення;

Завдання проекту:

•    виміряти лінійні розміри пакетів із соком, обчислити їх об’єми, порівняти із об’ємами, заявленими виробником;
•    навчитися виконувати переведення системних одиниць об’єму в несистемні, читати маркування об’ємів на упаковках різних товарів;
•    ознайомитися із економічною теорією граничної корисності, дією закону спадної граничної корисності;
•    визначити, як покупцеві краще здійснити вибір товару, обґрунтувати доцільність і раціональність цього вибору;
•    захистити проект на відкритому занятті з математики.

Учасники проекту: студенти другого курсу коледжу.

Тривалість проекту: 1 тиждень.

Навчальні предмети, інтегровані в проекті: математика, економіка, інформатика.

Обладнання: пакети із соком «Садочок» різних об’ємів, вимірювальні та обчислювальні прилади, мультимедійний комплекс.

Форма презентації: відкрите заняття з математики із звітуванням про результати роботи.

Запрошені на презентацію проекту: студенти, викладачі, адміністрація.

ОПИС ПРОЕКТУ

І. ВИЗНАЧЕННЯ НАПРЯМКІВ ДІЯЛЬНОСТІ. ЗАВДАННЯ ДЛЯ ГРУП.

Для створення проекту з групи студентів було сформовано три відділи:

1. Відділ вимірювань.
2. Відділ стандартизації.
3. Відділ маркетингу.

Завдання для відділу вимірювань:

•    придбати упаковки (тетра пак) соку «Садочок» об’ємами  0,2 л;  0,5 л;  1 л;  1,5 л  та 2 л.
•    виміряти лінійні розміри пакетів (довжину, ширину та висоту) в см.
•    обчислити об’єми пакетів у см³.
•    перевести см³ у дм³ (в літри).
•    порівняти обчислений об’єм з об’ємом, заявленим виробником.

Завдання для відділу стандартизації:

•    розробити алгоритм переведення кратних лінійних одиниць довжини вимірювання в квадратні одинці (площі) та кубічні одиниці (об’єму).
•    зробити висновки. Результати переведення подати у вигляді таблиці:

Завдання для відділу маркетологів:

•    порівняти вартість упаковок соку «Садочок» різного об’єму.
•    визначити найбільш раціональний вибір споживчої поведінки в балансі «об’єм – ціна».
•    перевірити дію закону спадної граничної корисності (першого закону Госсена).
•    надати рекомендації до «розумного» вибору соку для споживача.
•    результати досліджень подати у вигляді таблиць та діаграми вартості 6 л соку.

ІІ. РЕАЛІЗАЦІЯ МЕТИ ТА ЗАВДАНЬ ПРОЕКТУ.

«Співробітники» відділів протягом тижня:

•    працюють над виконанням запланованих завдань;
•    консультуються з фахівцями – викладачами математики та економіки коледжу;
•    створюють мультимедійні презентації для захисту проекту.

ІІІ. ПРЕЗЕНТАЦІЯ - ЗАХИСТ РЕЗУЛЬТАТІВ ПРОЕКТУ.

Учасники проекту захищають свої роботи, презентуючи результати на відкритому занятті з математики.

Результати досліджень відділу вимірювань

1. Придбати упаковки (тетра пак) соку «Садочок» об’ємами  0,2 л;  0,5 л;  1 л;  1,5 л  та 2 л.
2. Виміряти лінійні розміри пакетів (довжину, ширину та висоту) в см.
3. Обчислити об’єми пакетів у см³.
4. Перевести см³ у дм³ (в літри).
5. Порівняти обчислений об’єм з об’ємом, заявленим виробником.
6. Обчислити відносну похибку вимірювань 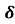за формулою

= 100% ,

 де - об’єм, заявлений виробником, – об’єм, обчислений за результатами вимірювань.

7. Результати вимірювань занести до таблиці:

№ досліду	лінійні розміри пакету, см			Об’єм пакету  V=abc, см3	Об’єм пакету в літрах (дм3)	об’єм, заявлений виробником, л	Відносна похибка вимірювань, %
	довжина a, см	ширина b, см	висота c, см
1	6,3	3,8	8,3	198,702	0,199	0,2	0,5
2	7,5	4,9	14,5	532,875	0,533	0,5	6,6
3	9,2	5,4	19,3	958,824	0,959	0,95	0,9
4	9	6,5	24,5	1433,25	1,433	1,45	0,9
5	11,3	7,2	23,9	1944,504	1,94	1,93	0,5

8. Висновки.

Обчислені об’єми упаковок соку за результатами дослідних вимірювань відповідають об’ємам, заявленим виробником. Похибка складає 0,5 – 0,9 %, що може буде пов’язане із товщиною матеріалу упаковки (тришаровий тетра пак) та похибкою вимірювальних приладів.

Звіт відділу маркетингу

1. Порівняти вартість упаковок соку «Садочок» різного об’єму.

Вартість упаковок соку «Садочок», заявлена продавцем торгівельної мережі:

об’єм	0,2 л	0,5 л	0,95 л	1,45 л	1, 93 л
вартість	6,71 грн	13,02 грн	19,66 грн	28,48 грн	36 грн

2. Визначити найбільш раціональний вибір споживчої поведінки в балансі «об’єм – ціна».
3. Перевірити дію закону спадної граничної корисності (першого закону Госсена).
4. Надати рекомендації до «розумного» вибору соку для споживача.
5. Результати досліджень подати у вигляді таблиць та діаграми вартості 6 л соку:

№ досліду	Порівняння упаковок	Порівняння об’ємів та ціни	Порівняння вартості	Висновки
1	0,2 л і 0,5 л	0,2 л х 2 = 0,4 л 6,71 грн х 2 =  13,42 грн	0,4 л = 13,42 грн 0,5 л = 13,02 грн	2 упаковки по 0,2 л мають менший на 20% об’єм і більшу на 3% вартість
2	0,2 л і 0,95 л	0,2 л х 5 = 1 л 6,71 грн х 5 = 33,55 грн	1 л = 33,55 грн 0,95 л = 19,66 грн	5 упаковок по 0,2 л мають більший на 5% об’єм і більшу на 41% вартість
3	0,2 л і 1,45 л	0,2 л х 7 = 1,4 л 6,71 грн х 7 = 46,97 грн	1,4 л = 46,97 грн 1,45 л = 28,48 л	7 упаковок по 0,2 л мають менший на 3% об’єм і більшу на 65% вартість
4	0,2 л і 1,93 л	0,2 л х 10 = 2 л 6,71 грн х 10 = 67,10 грн	2 л = 67,10 грн 1,93 л = 36 грн	10 упаковок по 0,2 л мають більший на 4% об’єм і більшу на 86% вартість
5	0,5 л і 0,95 л	0,5 л х 2 = 1 л 13,02 грн х 2 = 26,04 грн	1 л = 26,04 грн 0,95 л = 19,66 грн	2 упаковки по 0,5 л мають більший на 5% об’єм і більшу на 32% вартість
6	0,5 л і 1,45 л	0,5 л х 3 = 1,5 л 13,02 грн х 3 = 39,06 грн	1,5 л = 39,06 грн 1,45 л = 28,48 грн	3 упаковки по 0,5 л мають більший на 3% об’єм і більшу на 37% вартість
7	0,5 л і 1,93 л	0,5 л х 4 = 2 л 13,02 грн х 4 = 52,08 грн	2 л = 52,08 грн 1,93 л = 36 грн	4 упаковки по 0,5 л мають більший на 4% об’єм і більшу на 45% вартість
8	0,95 л і 1,45 л	0,95 л х 3 = 2, 85 л 19,66 грн х 3 = 58,98 грн 1,45 л х 2 = 2,9 л 28,48 грн х 2 = 56,96 грн	2,85 л = 58,98 грн 2,9 л = 56,96 грн	три літрових упаковки коштують на 4% дорожче за дві 1,5-літрових
9	0,95 л і 1,93 л	0,95 л х 2 = 1,9 л 19,66 грн х 2 = 39,32 грн	1,9 л = 39,32 грн 1,93 л = 36 грн	дві літрові упаковки дорожчі за одну 2-літрову на 9%
10	1,45 л і 1, 93 л	1,45 л х 4 = 5,8 л 28,48 грн х 4 = 113,92 грн 1,93 л х 3 = 5,79 л 36 грн х 3 = 108 грн	5,8 л = 113,92 грн 5,79 л = 108 грн	Чотири 1,5-літрові упаковки дорожчі за три 2-літрові на 5%

Вартість 6 л соку «Садочок» в різних упаковках:

об’єм	0,2 л (30 упаковок)	0,5 л (12 упаковок)	0,95 л (6 упаковок)	1,45 л (4 упаковки)	1, 93 л (3 упаковки)
вартість	201,30 грн	156,24 грн	117,96 грн	113,92 грн	108 грн

 

Висновки:

• чим більший об’єм соку, тим дешевша ціна упаковки;
• найдорожчою для покупців буде придбання декількох упаковок соку об'ємом 0,2 л. 1 л соку в такій упаковці коштуватиме на 40% дорожче ніж одна літрова упаковка, а 6 л – майже вдвічі дорожче;
• три літрових упаковки коштують майже стільки, скільки дві півторалітрових. Тому вигідніше купляти літровий пакет, щоб не переплачувати;
• відповідно до закону спадної граничної корисності користь кожної додаткової одиниці зменшується, тому корисність  третього літрового пакету соку буде менша, ніж другого півторалітрового. Ще один доказ, що при приблизно однаковій вартості товару, раціональний споживач вибере товар в меншій упаковці;
• виробнику вигідно випускати продукцію в більшій тарі – це економія виробничих ресурсів, зарплатні, податків. Проте, якщо спрагу потрібно вгамувати тут і зараз, то покупцеві необхідний маленький пакетик соку, він не буде мати справу з великими упаковками, які нададуть йому масу додаткових незручностей, і за яку він заплатить більше. Тому виробники на маленьких об’ємах завищують ціну, аби покрити видатки.

Результати досліджень відділу стандартизації

1. Розробити алгоритм переведення кратних лінійних одиниць довжини вимірювання в квадратні одинці (площі) та кубічні одиниці (об’єму).
2. Результати переведення подати у вигляді таблиці:

одиниці	метр	дециметр	сантиметр	міліметр	кілометр
множник	1	0,1 = 10 -1	0,01 = 10 -2	0,001 = 10 -3	1000 = 10 3
лінійні	1	10 -1	10 -2	10 -3	10 3
квадратні	12	(10 -1)2 = 10 -2	(10 -2)2 = 10 -4	(10 -3)2 = 10 -6	(10 3)2 = 10 6
кубічні	13	(10 -1)3 = 10 -3	(10 -2)3 = 10 -6	(10 -3)3 = 10 -9	(10 3)3 = 10 9

 

3. За поданим алгоритмом навести приклади переведення:

5 см = 5 * 10 ^-2 м = 5 * 0,01 = 0,05 м

5 см² = 5 * (10 ^-2) ² = 5 * 10 ^-4 = 5 * 0, 0001 = 0,0005 м²

5 см³ = 5 * (10 ^-2) ³ = 5 * 10 ^-6 = 5 * 0, 000001 = 0,000005 м²

 

71 дм = 7,1 м

71 дм² = 71 * 10 ^-2 = 0,71 дм²

71 дм³ = 71 * 10 ^-3 = 0,071 дм³

 

54 мм = 54 * 10 ^-3 = 0,054 м

54 мм² = 54 * 10 ^-6 = 0,00054 м²

54 мм³ = 54 * 10 ^-9 = 0,000000054 м

 

6,53 км = 6,53 * 10 ³ = 6530 м

6,53 км² = 6,53 * 10 ⁶ = 6530000 м²

6,53 км³ = 6,53 * 10 ⁹ = 6530000000 м³

4. Висновки:

• для переведення кратних лінійних одиниць в основні треба кратну одиницю помножити на відповідний множник;
• для переведення кратних квадратних одиниць (площі) в основні треба кратну одиницю помножити на відповідний множник, піднесений до квадрата;
• для переведення кратних кубічних одиниць (об'єму) в основні треба кратну одиницю помножити на відповідний множник, піднесений до куба.

рисунок 10. Проєкт «Об'єм соку» (публікауція на платформі ВСЕОСВІТА)

 

Діаграми та графіки

Задачі на діаграми та графіки можна використовувати під час ваивчення тем, пов'язаних із дослідженням функцій, математичної статистики, відсоткових розрахунків.

рисунок 11. Практична робота «Моя успішність за семестр»

Практична робота

Тема: «МОЯ УСПІШНІСТЬ ЗА СЕМЕСТР»

(«Елементи математичної статистики»)

Мета: Узагальнити та систематизувати знания з теми «Елементи математичної статистики», навчитися обробляти статистичні дані, знаходити вибіркові характеристики, центральні тенденції вибірки, візуалізувати аналітичну інформацію.

 

Хід роботи

 

1. Із залікової книжки виписати оцінки з усіх предметів за перший семестр - це буде статистична вибірка.

Оцінки: ______________________________________________________________

2. Впорядкувати дану вибірку:

__________________________________________________________________

3. Визначити об’єм та розмах вибірки:

Об’єм вибірки
Розмах вибірки

4. Скласти частотну таблицю:

елемент (оцінка)	12	11	10	9	8	7	6	5	4
частота

5. Побудувати гістограму виборки (стовпчасту діаграму). Можна побудувати від руки, можна за в графічному редакторі EXCEL. Навчальне відео за посиланням https://www.youtube.com/watch?v=vnnMHBdqRtI .

6. Знайти центральні тенденції вибірки (моду, медіану, середнє значення)

Середнє значення
мода
медіана

7. Побудувати в графічному редакторі EXCEL кругову діаграму виборки. Навчальне відео за посиланням https://www.youtube.com/watch?v=y_OXooIKCrw.

8.  Кругову діаграму розмістити на Padlet за посиланням https://uk.padlet.com/chinovata/padlet-yq52sc29137yu4y2
9. Зробити  висновок, в якому проаналізувати свою успішність: якій рівень навчальних досягнень (початковий, середній, достатній або високий), які оцінки переважають, які предмети краще даються, над яким треба ще попрацювати, що підтягнути, як покращити успішність в наступному семестрі.

Висновок

 

рисунок 12. Практична робота «Моя успішність за семестр» (публікація на платформі На Урок)

 

Маршрут за гугл картою

рисунок 12. Маршрут за гугл картою

Такі задачі ми вирішуємо щодня (рис.12). Хоча і сучасні гугл карти достатньо досконало і повно прокладають маршрути, проте і тут є місце, де можна студентам прикластися і попрацювати. Спробуємо скласти маршрут вихідного дня, де ми хочемо відвідати три об’єкти. Потрібно скласти маршрути для пішої прогулянки, для пересування на міському транспорті, для поїздки на замовленому автобусі. Запропонуйте прорахувати час подорожі, довжину маршруту, вартість в залежності від обраного способу пересування. (Всю додаткову інформацію щодо вартості проїзду, пробок тощо гугл карта надає).

 

Навігатор?!

рисунок 13. Навігатор

Цей гаджет є незамінним помічником водіїв та пішоходів, особливо коли пересуваємося в незнайомій місцевості (рис.13). Який матеріал може дати навігатор для математичної компетентнісної задачі?

По-перше, можна повторити всі види кутів:

• поверніть праворуч(ліворуч) – на 90 градусів, прямий кут;
• плавний поворот праворуч (ліворуч) – тупий кут;
• з’їзд праворуч (ліворуч), різкий поворот, тримайтеся ліворуч (праворуч) – гострий кут;
• виконайте розворот  - розгорнутий кут, 180 градусів.

По-друге, коли маршрут змінено, можна прорахувати зміну відстані, економію часу тощо. Найчастіше в таких задачах буде використовуватися теорема Піфагора – зрізати кут, піти навпростець, на математичній мові – по гіпотенузі!

 

Дорожні знаки

рисунок 14. Дорожні знаки

За допомогою знаків дорожнього руху (рис.14) можна вивчати такі теми з геометрії:

• многокутники, їх властивості;
• паралельні та перпендикулярні прямі;
• вектори та їх властивості;
• кути, ламана;
• коло і круг;
• вписані та описані многокутники.

В дорожніх знаках всі ці поняття зашифровані. Можна дати завдання придумати свій знак дорожнього руху, який буде складатися з певних геометричних фігур, пояснити актуальність такого вибору.

 

Ремонт в оселі

Задачі на многогранники, на обчислення їх площі поверхонь та об’ємів – це найпрактичніші задачі, які доводиться розв’язувати всім, хто починає робити ремонт.  Пофарбувати стелю або стіни, покрити підлогу, заповнити водонагрівач або басейн водою, залити фундамент будівлі, перекрити дах, скласти сіно в стозі тощо. Як правило, на практиці ці задачі потрібні для кошторису, проте їх не складеш, поки не розв’яжеш геометричну задачу, пов’язану із вимірами величин та обчислення їх параметрів за допомогою математичних формул. Лайфхак: модель кімнати можна скласти за допомогою магнітного конструктору (рис.15).

рисунок 15. Ремонт в оселі

 

Задачі за професійним спрямуванням

рисунок 16. Задачі за професійним спрямуванням

 

Як поєднати фізику і мистецтво?

Культурологія та фізика: гармонійний тандем.

 Творчість Леонардо да Вінчі

студентський інтегрований творчій проєкт

        Проєктна діядьність – насьогодні найефективніший метод формування навчальних компетенцій, критичного мислення та м’яких навичок. Творчій інтегрований проєкт з предметів фізика та культурологія поєднує вивчення художньої творчості Леонардо да Вінчі та його технічні винаходи. Підсумок проєкту - відтворена через 500 років (!) інженерна задумка майстра, зібраний міст Леонардо да Вінчі судентами власноруч!

ПАСПОРТ ПРОЄКТУ

Актуальність проєкту: довкола постаті Леонардо да Вінчі зацікавлення не вщухає сотні років, із геніями завжди так — відстань у часі не віддаляє: його картини, винаходи, думки досі актуальні і захопливі. Леонардо да Вінчі вивчив наукову базу мистецтва Ренесансу (перспективу, світло, пропорції, анатомію тощо) і використав її майже в  кожному аспекті дослідження природи. Він бачив мистецтво як граничну форму візуального знання, заснованого на розумінні принципів устрою навколишнього світу. У всіх своїх починаннях майстер шукав суть математичних правил (математику, статистику, динаміку), які регулюють все, що відбувається у Всесвіті. Адже вони наказують, яким чином ми маємо втілювати природу в мистецтві, науці та технології. Кожне технічне пристосування можна сприймати як нове тіло, чий зліпок взятий зі світу, але не імітований безпосередньо. Раніше ніхто не робив нічого схожого.

Цілі проекту та очікувані результати:

•    ознайомитися з видами простих механізмів: важіль, колесо, похила площина, гвинт, блок, клин, тощо;
•    вивчити їх принцип дії, застосування у побуті;
•    ознайомитися із творчістю Леонардо да Вінчі, його винаходами та інженерно-технічними ідеями;
•    за допомогою мобільного додатку із доповненою реальністю відтворити принцип роботи механізмів да Вінчі;
•    власноруч зібрати міст Леонардо да Вінчі;
•    вдосконалити вміння презентувати себе та результати своєї роботи;
•    розвинути здатність студентів до самоосвіти та самовдосконалення, вміння підвищити свою свідомість та самооцінку;
•    сформувати почуття відповідальності за виконання своєї роботи та роботи команди і всього проекту в цілому;
•    розвинути здатність логічно обґрунтовувати власну позицію та приймати виважені рішення;

Завдання проекту:

•    ознайомитися із принципом дії простих механізмів, обґрунтувати їх роботу з точку зору законів фізики;
•    вивчити принцип дії  винаходів Леонардо да Вінчі, за допомогою мобільного додатку Da Vinci Machines із доповненою реальністю відтворити роботу його пристроїв: самохідного танку, гвинтокрила, катапульти;
•    на занятті з культурології провести панельну дискусію з питань життя та творчості Леонардо да Вінчі, переглянувши художній фільм «Леонардо. Незвідані світи» (2019);
•    встановити причинно-наслідкові зв’язки між художньою та технічною творчістю Леонардо да Вінчі;
•    власноруч зібрати міст Леонардо да Вінчі, який за життя майстра так і не був збудований;
•    захистити проект на відкритому інтегрованому занятті з фізики та культурології.

Учасники проекту: студенти другого курсу коледжу.

Тривалість проекту: 1 тиждень.

Навчальні предмети, інтегровані в проекті: фізика, культурологія, мистецтво, всесвітня історія.

Обладнання: мобільний додаток з доповненою реальністю Da Vinci Machines, дерев’яні палички та дерев’яний брус для збирання мосту

Форма презентації: інтегроване відкрите заняття з фізики та культурології із звітуванням про результати роботи, презентація проекту на тематичних конференціях.

Запрошені на презентацію проекту: студенти, викладачі, адміністрація, учасники конференцій.

ОПИС ПРОЕКТУ

І. ВИЗНАЧЕННЯ НАПРЯМКІВ ДІЯЛЬНОСТІ. ЗАВДАННЯ ДЛЯ ГРУП.

Для створення проекту з групи студентів було сформовано три відділи:

4. Художній відділ.
5. Технічний відділ.
6. Організаційний відділ.

Завдання для художнього відділу:

•    вивчити життєвий та творчий шлях Леонардо да Вінчі.

•    за результати перегляду художнього фільму «Леонардо да Вінчі. Незвідані світи» (2019) скласти проблемні питання для обговорення на панельній дискусії;

•    скласти план проведення панельної дискусії;
•    створити тематичні питання для вікторини за результатами обговорення фільму;

Завдання для технічного відділу:

•    ознайомитися із мобільним додатком з доповненою реальністю Da Vinci Machines;
•    за допомогою додатку відтворити роботу винаходів Леонардо да Вінчі: самохідного танку, катапульти, гвинтокрила, з’ясувати їх принцип роботи;
•    вивчити оригінальні креслення технічних ідей Леонардо да Вінчі, скориставшись оцифрованим блокнотом майстра «The Codex Arundel», який виклала у вільний доступ Британська бібліотека;
•    власноруч зібрати міст Леонардо да Вінчі.

Завдання для організаційного відділу:

•    організувати проведення панельної дискусії за результатами перегляду художнього фільму «Леонардо да Вінчі. Незвідані світи».
•    ознайомитися з правилами проведення панельних дискусій, навчитися модерувати подібні заходи;
•    згенерувати план презентації проєкту, узгодивши його з технічним та художнім відділами;
•    забезпечити технічну підтримку презентації проєкту.

ІІ. РЕАЛІЗАЦІЯ МЕТИ ТА ЗАВДАНЬ ПРОЕКТУ.

«Співробітники» відділів протягом тижня:

•    працюють над виконанням запланованих завдань;
•    консультуються з фахівцями – викладачами фізики та культурології коледжу;
•    створюють мультимедійні презентації для захисту проекту, збирають міст да Вінчі.

ІІІ. ПРЕЗЕНТАЦІЯ - ЗАХИСТ РЕЗУЛЬТАТІВ ПРОЕКТУ.

Учасники проекту захищають свої роботи, презентуючи результати на відкритому інтегрованому занятті з фізики та культурології.

   

рисунок 17. Міст да Віінчі

рисунок 17. Посилання на відео збирання мосту да Вінчі

Підлітковий екстрім з точки зору математики: чи варто?

рисунок 18. Підлітковий екстрім

ПІДЛІТКОВИЙ ЕКСТРІМ З ТОЧКИ ЗОРУ МАТЕМАТИКИ: ЧИ ВАРТО?

(студентський дослідницький проект)

ПАСПОРТ ПРОЄКТУ

Актуальність проєкту: у підлітків та нейронна мережа, яка відповідає за обдуманість рішень, ще не сформувалася остаточно. Проте та нейронна мережа, яка відповідає за ризик і імпульсивність, вже функціонує щосили. Тому ще зовсім юні створіння вибирають екстрим! Причиною є також важкі переживання, які кожен підліток відчуває в перехідному віці, а бажання випробувати себе на міцність - це лише спосіб відволіктися від психо-емоційного напруження. Якщо дорослі віддають перевагу «полоскотати собі нерви», все ж підстраховуючись за допомогою гарного спорядження, то підлітки в цьому плані нерозумні - виконують небезпечні трюки без усякої страховки.

Цілі проекту та очікувані результати:

•    ознайомитися з видами екстремальних розваг підлітків;
•    відтворити математичні моделі поведінкових ситуацій в екстремальних умовах;
•    за математичними моделями – графіками функцій проаналізувати ризики екстремальних розваг;
•    довести небезпечність ризикової поведінки;
•    переконатися і підсумувати, що життя – це найбільша цінність, яка дана людині, а найголовнішим скарбом життя є здоров’я;
•    вдосконалити вміння презентувати себе та результати своєї роботи;
•    розвинути здатність студентів до самоосвіти та самовдосконалення, вміння підвищити свою свідомість та самооцінку;
•    сформувати почуття відповідальності за виконання своєї роботи та роботи команди і всього проекту в цілому;
•    розвинути здатність логічно обґрунтовувати власну позицію та приймати виважені рішення;

Завдання проекту:

•    вивчити небезпечні ситуації, в яких опиняються підлітки задля адреналіну чи за необізнаності наслідками: стрибок з висоти, перебігання перед автомобілем, що рухається, катання на даху електропотягу;
•    описати математично моделі цих ситуацій;
•    зробити графічну інтерпретацію залежності висоти стрибку з висоти, гальмівного шляху автомобіля, напруженості електричного поля на контактному дроті високовольтної лінії
•    проаналізувати графіки, зробити висновки;
•    захистити проект на відкритому занятті з математики.

Учасники проекту: студенти першого курсу коледжу.

Тривалість проекту: 1 тиждень.

Навчальні предмети, інтегровані в проекті: фізика, хімія, біологія, інформатика.

Обладнання: ноутбук, мобільні додатки, веб камера

Форма презентації: відкрите заняття з математики із звітуванням про результати роботи.

Запрошені на презентацію проекту: студенти, викладачі, адміністрація.

ОПИС ПРОЕКТУ

І. ВИЗНАЧЕННЯ НАПРЯМКІВ ДІЯЛЬНОСТІ. ЗАВДАННЯ ДЛЯ ГРУП.

Для створення проекту з групи студентів було сформовано три наукових товариства:

7. Гравітація.
8. Динаміка.
9. Електрика.

Завдання для наукового товариства «Гравітація»:

•    вивчити математично-фізичні аспекти стрибка з висоти;
•    описати стрибок як поводження тіла, що вільно падає;
•    створити математичну модель даної ситуації, побудувати графік залежності швидкості тіла від висоти, з якої воно падає;
•    довести небезпеку такої розваги.

Завдання для наукового товариства «Динаміка»:

•    вивчити математично-фізичні аспекти перебігання перед автомобілем, що рухається на швидкості.
•    описати гальмування автомобіля як поводження тіла, що рухається рівносповільнено;
•    створити математичну модель даної ситуації, побудувати графік залежності гальмівного шляху автомобіля від швидкості, з якою він рухається;
•    довести небезпеку такої поведінки.

Завдання для наукового товариства «Електрика»:

•    вивчити математично-фізичні аспекти прогулянок на даху електропотягу, що рухається.
•    описати принцип дії високовольтного контактного дроту як створене ним електричне поле;
•    створити математичну модель даної ситуації, побудувати графік залежності напруженості електричного поля від відстані до лінії електропередач;
•    довести небезпеку такої поведінки.

ІІ. РЕАЛІЗАЦІЯ МЕТИ ТА ЗАВДАНЬ ПРОЕКТУ.

Члени товариств протягом тижня:

•    працюють над виконанням запланованих завдань;
•    консультуються з фахівцями – викладачами фізики та теоретичної механіки коледжу;
•    готують доповіді для захисту проектів.

ІІІ. ПРЕЗЕНТАЦІЯ - ЗАХИСТ РЕЗУЛЬТАТІВ ПРОЕКТУ.

Учасники проекту захищають свої роботи, презентуючи результати на відкритому занятті з математики.

ДОВІДКОВІ МАТЕРІАЛИ

СТРИБОК З ВИСОТИ

        Дослідження та статистика свідчать, що при стрибкові з висоти під час зіткнення із землею на швидкості 30 км/год імовірність виживання становить 95%. За швидкості 50 км/год цей показник становить 20%. На більшій швидкості настає миттєва смерть або тяжкі тілесні ушкодження.

          В фізиці залежність швидкості v від висоти h, з якої падає тіло, виражається формулою:

,

де g = 10 м/с² – прискорення вільного падіння.

Розрахуємо, на якій висоті повинно знаходитися тіло, щоб воно рухалося із швидкістю 30 км/год = 8,3 м/с:

8,3 =

68,89 = 20 h

h = = 3,44 м

Стрибаючі з висоти 3,5 м (не вище другого поверху) є надія залишитися живим і відносно «цілим». Це гарантують ті 95 статистичних відсотків.

             Тепер обчислимо аналогічно висоту для швидкості 50 км/год = 14 м/с:

14 =

196 = 20 h

h = = 9,8 м

А якщо стрибати з висоти 10 м – практично нульова гарантія вижити!

              Побудуємо графік залежності швидкості від висоти. Математично це буде коренева функція , графіком якої є вітка параболи:

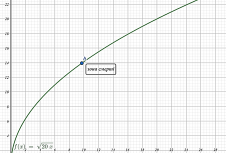
                  Точка А (14; 9,8) – точка неповернення! Далі – смерть!

 

ГАЛЬМІВНИЙ ШЛЯХ

                   Гальмівний шлях автомобіля залежить від багатьох чинників: від його швидкості, коефіцієнту тертя, коефіцієнту гальмування. У реальному житті для визначення гальмівного шляху використовується формула, виведена експериментальним шляхом:

, де

           d – гальмівний шлях

           k – коефіцієнт гальмування

v – швидкість автомобіля

µ - коефіцієнт зчеплення з дорогою.

         Коефіцієнт гальмування k = 1 для легковиків, для вантажівок k 1. Коефіцієнт зчеплення з дорогою µ залежить від погодних умов на дорозі:

            µ = 0,7 – суха дорога

            µ = 0,4 – мокра дорога

µ = 0,2 – засніжена дорога

µ = 0,1 – ожеледиця.

        Виведемо формулу залежності легковика на сухій дорозі від його швидкості.

=

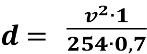 Напишемо її в математичному вигляді: .

На графіку – це парабола. Побудуємо її.

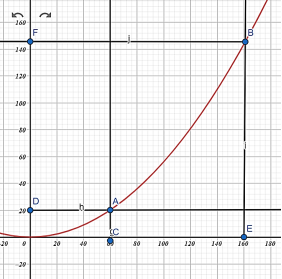
Аналізуючи графік, бачимо, що при швидкості 60 км/год (точка С) гальмівний шлях становить 20 м (точка D). А при швидкості 160 км/год (точка Е) – вже 145 м (точка F)!!!!

           Тепер проаналізуємо гальмівний шлях вантажівки в ожеледицю. Формула буде мати вигляд, наприклад,

.

Побудуємо цю параболу:

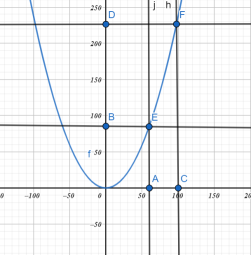
З графіка видно, що при швидкості 60 км/год у вантажівки гальмівний шлях вже складає, не 20 м, як у легковика, а цілих 90 м! А якщо ж розженеться до 100 км/год, тоді зупиниться аж через 230 м!

         В формулу гальмівного шляху не закладено масу автомобіля, знос шин та гальм, що може ще збільшити гальмівний шлях.

        Робіть висновки, як же ж треба безпечно переходити дорогу!

ЗАЦЕПІНГ

            ЩО ЦЕ: катання на поїздах, електричках, трамваях і метро зовні вагона.

            За суттю те ж саме, що й трейнсерфінг (train+surfing) – вільне пересування на поїздах та інших видах рейкового транспорту, тільки назва «наша». Вважається, що цей спосіб виник з часу появи залізниць, а у воєнні та післявоєнні роки навіть був обумовлений об’єктивною потребою: в переповнених потягах просто не вистачало місць. Втім, в Індії досі курсують «смертельні поїзди»: місцеві обсідають дахи чи гронами повисають зовні, через що неминуче гинуть  8-10 осіб на день.

              Деколи зацепери їздять «поза вагонами», аби не платити за квитки, але частіше задля гострих вражень. Відчайдушні підлітки хапаються за поручні і решітки, вилазять на східці і міжвагонні зчеплення, влаштовуються на буферах та інших «придатних» частинах.

             Професіонали (є й такі!) використовують спеціальне екіпірування: страхувальні ремені, карабіни, вакуумні присоски, захисні маски. Але нажаль, аматорів набагато більше: вони зриваються під час руху, зіштовхуються зі стовпами і тунельними конструкціями, гинуть від дотику до високовольтних шин і падають під колеса.

      Високовольтні лінії електропередач (ЛЕП), якими живляться електропотяги, достатньо потужні, вони мають велику напругу, а тому створюють навколо себе потужне електричне поле. По мірі віддалення від ЛЕП напруженість такого поля зменшується. Людське тіло є добрим провідником електрики, і тому, за законами фізики, при наближенні до ЛЕП може виникнути пробій шару повітряного діелектрика, і через ваш організм починає проходити електричний струм. В такому випадку людину вражає електричним струмом навіть без доторкання до струмоведучих елементів.

       Розрахуємо небезпечну відстань, на якій можна знаходитися біля ЛЕП.

       Напруженість електричного поля  Е  обчислюється за формулою

E = ,

де U – напруга,  d – відстань до контактного дроту.

         На залізниці напруга може досягати 27 000 В, або 27 кВ. Побудуємо графік залежності напруженості електричного поля від відстані до лінії електропередачи.

          Математична модель даної задачі має вигляд функції   у = . Графіком цієї функції є гіпербола.

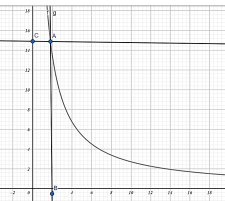
             Гранично допустимі рівні напруженості електричного поля в незаселеній місцевості складають 15 кВ/м. Аналізуючи графік, бачимо, що така напруженість поля буде на відстані 2 м. Тобто більше, ніж на 2 м наближатися до ЛЕП небезпечно. Ось чому мандруючи на дахові електропотягу, навіть не контактуючи з електричними дротами, можна бути ураженим електричним струмом, і все закінчиться трагедією.

             Дбайте про своє життя! Не піддавайте його ризику смерті!

 

Скільки років Діофанту?

рисунок 19. Скільки років Діофанту?

Український письменник Іван Якович Франко перекладав українською мовою віршовані задачі давньогрецьких математиків, а деколи і сам шукав способи їх розв’язання. Ось одна з таких задач (рис.19). ЇЇ автор філософ Метродор Хіосський пропонує порахувати, скільки років прожив грецький математик Діофант Олександрійський. Про життя   Діофанта відомо лише з цього допису. Рядки вірша були викарбувані на могильній плиті математика.

 

Задачі за Книгою Рекордів України

В Україні існує своя книга рекордів, аналогічна Книзі рекордів Гінеса. Хіба люди з цієї книги та їх досягнення не є приводом гордості за співвітчизників? Аби студенти дізналися про них, я запропонувала  ознайомитися  з цією книгою. А щоб студенти не були просто спостерігачами чужих досягнень, а почали шлях до своїх, я запропонувала скласти та розв’язати задачі, пов’язанні  з рекордами українців. Було влаштовано конкурс на кращі задачі, відзначено переможців. Найкращі роботи пропоную до вашої уваги.   

Математичні задачі за книгою рекордів України

1. Андрій Косташ з Києва за 1 годину віджався 1670 разів. Потім його темп зменшився: за 2 наступних години він зробив 2950 віджимань. На скільки відсотків зменшилась швидкість віджимань Андрія. Відповідь округлити до сотих. (Відповідь: .)
2.  Київські кухари в самому центрі столиці, на майдані  Незалежності, приготували найдовший шашлик на одному шампурі не тільки в Україні, а й у всьому світі. Його довжина склала 150,6 м, а на приготування пішло 180 кг м’яса. Скільки людей змогли покуштувати шашлик, та який прибуток від його продажу отримали кухари, якщо порція (100 г) коштувала 40 грн. Вважати, що м'ясо при обробці втрачає 27% своєї маси. (Відповідь: 1314 людей, 52560 грн.)
3. В Києві дівчата спекли гарбузовий пиріг-велетень вагою 240 кг. Скільки людей поласує пирогом, якщо вага однієї порції 120 г. (Відповідь: 2000 людей.)
4. Випускник Харківської загальноосвітньої школи І-ІІІ ступенів № 58 Денис Ткемеладзе за 11 років навчання не пропустив жодного уроку в школі по всіх предметах. Скільки часу проводив Денис в школі за місяць (20 навчальних днів), якщо за розкладом щодня 7 уроків по 45 хв. кожний. (Відповідь: 105 год.)
5.  Надія Колесникова потрапила до книги рекордів України як найвища людина в Україні. Коли вона стоїть на каблуках її зріст дорівнює 229 см. Зріст Володимира Зеленського складає 72,5 % від зросту Надії. Який зріст Володимира Зеленського? (Відповідь: 166 см.)
6. Засновник і президент Київського міського автомотоклубу Сергій Малик встановив рекорд України, розігнавши свій болід класу «Формула» на льодовому шоу столичного озера Сонячне до 112 км/год. Анатолій Єфімов, відомий мотогонщик, майстер міжнародного класу, на цій трасі встановив іще один абсолютний рекорд України. Він розігнав мотоцикл Suzuki RMZ 250 R до позначки 116 км/год. Хто з рекордсменів та на скільки хвилин проїде відстань у 1000 км швидше? (Відповідь: Єфімов, на 18,6 хв.)
7.  Задумали деяке число. Якщо його піднести до квадрату та поділити на 2, то отримаємо вагу найбільшого випеченого в Україні капелюха. А якщо це число піднести до квадрату та додати 16, то вийде вік найстарішої українки. Вік жінки (в роках) у 2,32 рази більший за масу (у кг) капелюха. Знайти невідоме число, вік найстарішої жінки в Україні та вагу капелюха. (Відповідь: 10, 50 кг, 116 років.)
8. Якщо деяке число поділити навпіл, взяти від остачі 35%, потім ще половину, та від цієї остачі взяти третю частину, потім отримане число помножити на 0,2, то вийде 9,45. Знайшовши це число, отримаємо унікальне досягнення мешканця Миколаєва Олега Рички зафіксоване на фестивалі «Монгольф’єре» під Києвом. Піднявшись на повітряній кулі, він стрибнув із закритими очима з висоти, що дорівнює задуманому числу. З якої висоти стрибнув Олег Ричка? (Відповідь: 1620 м).
9.  Розв’язати рівняння: 6000х^-1 + х²*10^-2 = 601. Корені даного рівняння становлять вагу найбільшого гарбузового   пирога, що спекли в Україні (більший корінь) та кількість людей, які випікали його (менший корінь). (Відповідь: 240 кг та 10 людей).
10.  Дизайнерка-ювелір з Донецька Тетяна Калюжна отримала сертифікат про рекорд України як авторка найдорожчої шахтарської каски. ЇЇ оціночна вартість становить 42240 доларів США. Скільки років потрібно працювати шахтареві, аби заробити на цю каску, якщо середня зарплатня шахтаря 5632 грн/місяць, курс долара становить 1:8?  (Відповідь: 5 років).

         Даний конкурс та подібні до нього заходи сприяють духовному збагаченню українського студента, розвивають інтелектуальні здібності та почуття справжнього, не «паперового» або «ура» патріотизму, допомагають підвищити власну самооцінку та мотивацію навчання (рис.20).

рисунок 20. Задачі за Книгою Рекордів України

 

Калорійність їжі

Калорійна їжа – біда сучасного суспільства, ворог здоров’я, проблема багатьох хвороб. Проте практично на всіх продуктах харчування, які ми купляємо в магазинах, в меню всіх страв, які ми замовляємо в закладах громадського харчування, завжди вказано енергетичну цінність і склад цих продуктів.  Аби привчити молодь до раціонального харчування, потрібно складати задачі на розрахунок калорій, енергетичної та поживної цінності їжі, розрахунок індексу маси тіла, тощо (рис.21).

рисунок 21. Розрахунок калорійності їжі

 

Тренування та калорійність

Одна з наскрізних ліній компетентностей  «Здоров’я та безпека» передбачає формування у молоді здорового способу життя. На допомогу тут приходять різноманітні фітнес-трекери, які цілодобово знімають показники фізичної активності людини (рис.21). За цими показниками можна скласти величезну кількість компетентнісно орієнтованих задач. Можна навіть влаштувати конкурс на час тренувань, кількість спалених калорій, довжину дистанції бігу, ходьби, плавання тощо! Запропонуйте студентам розрахувати швидкість руху під час тренувань, проаналізувати показники тренувань і скласти їх оптимальний графік: в який день тижня, в яку пору доби тренування є найефективнішим. В тандемі із розрахунком калорійності можна слідкувати  і порівнювати отримані з їжею та втрачені із тренуванням калорії. Можна обчислити, скільки потрібно пробігти, аби з’їсти зайву шоколадку. З моєї практики потрібно пробігти аж цілих 5 км! Можна навіть заснувати перехідну щомісячну нагороду, яка буде вручатися найбільшому спалювачу калорій!

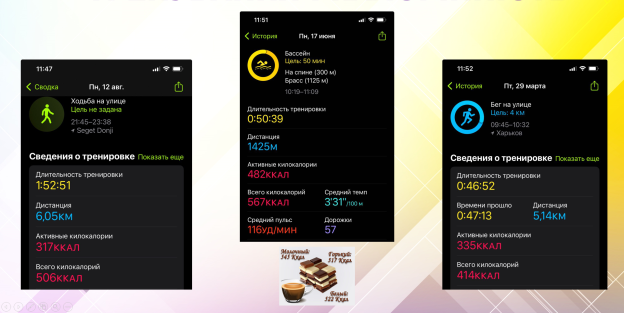
рисунок 22. Показники фітнес трекерів для компетентнісно орієнтованих задач

 

Електроенергія

Україна переживає дуже складне становище з енергозабезпеченням. Тарифи на електроенергію постійно зростають. Аби краще зрозуміти, чому так відбувається, і як виглядає Україна на тлі інших країн Європи, можна проаналізувати тарифи на електроенергію в Європейських країнах (рис.23).

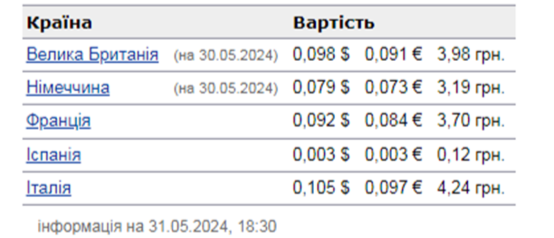
рисунок 23. Вартість електроенергії в різних валютах за 1 кВт*год

До інформації, поданої на рисунку 22, можна сформулювати такі запитання:

• найдорожчій і найдешевший тарифи;
• порівняти із тарифом в Україні;
• скільки відсотків від українського тарифу становить тариф в певній країні;
• обчислити місячну вартість в кожній країні при споживанні 500 кВт енергії за місяць;
• який відсоток становить ця плата від середньомісячної зарплаті в країні;
• різноманітні гістограми, кругові діаграми;
• центральні тенденції вибірки.

 

Стандартний вигляд числа

Числа, записані в стандартному вигляді, використовуються в багатьох галузях науки та виробництва, зустрічаються у повсякденному житті (рис.24). Часто доводиться переводити одиниці маси, довжини, об’єму в інші кратні одиниці. За допомогою стандартного вигляду можна записувати дуже великі і дуже малі величини. Без такого запису уявити їх неможливо. Неможливо оцінити розміри величезних та мініатюрних величин, які не вимірюються в звичайних умовах звичайними вимірювальними приладами. Вміння записувати числа в стандартному вигляді полегшує розв’язання задач з різних природничих дисциплін. Доцільно в математиці попрактикувати такі перетворення.

рисунок 24. Стандартний вигляд числа

 

Площа криволінійної трапеції

Здавалося б, що інтегральне числення – це суто теоретична математика, яку видумали абсолютно штучно, і уявити її в повсякденному житті неможливо. Насправді ще й яка практична! Не всі предмети  навколо нас мають форму чітких рівносторонніх або круглих геометричних фігур. Більшість з них - це криволінійні фігури. І найпростіша з них – криволінійна трапеція. А інші – це сума або різниця криволінійних трапецій (рис.25).

Як обчислили площу криволінійних материків? Як порахувати, скільки тканини потрібно купити на сукню фантастичного крою, а ціна  тканини – всі гроші світу? Який буде об’єм флакону вишуканої формі улюблених парфумів, щоб його можна було купити, якщо 1 мл цих парфумів також коштує всі гроші світу?

Ось тут на допомогу і прийде інтеграл. За його допомогою можна обчислити всі ці величини. Так, звичайно, нікому зараз на думку не спаде робити обчислення інтегралів вручну, коли комп’ютери зроблять це за лічені секунди.  А якщо раптом блекаут?..

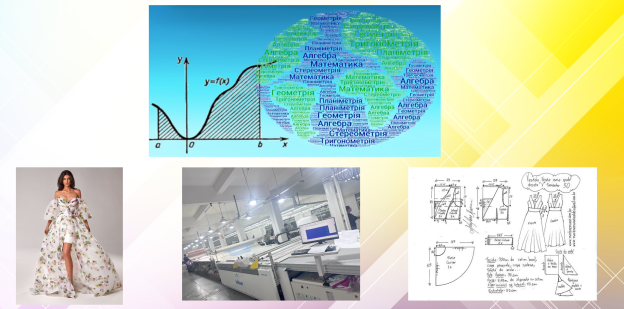
 рисунок 25. Площа криволінійної трапеції

 

Задачі від Юрія Захарійченка

Викладач математики Києво-Могилянської Академії Юрій Захарійченко проводить уроки математики «зі спецефектами». З будь якої життєвої ситуації він може скласти задачу: зоопарк, манікюр, хокей, вечірка, революція, поезія, політика, астрофізика, філософія (рис.26).

рисунок 26. Задачі від Юрія Захарійченка

Літня відпустка-подорож

Подорож у відпустці – це чудова нагода укласти власний міні (а може і мега?!) збірник компетентнісно-орієнтованих задач з математики. Умовами задачі може стати абсолютно все – починаючі від квитків на потяг і закінчуючи сувенірами на згадку:

• квитки на потяг (рис.27): відсоткова вартість різних зборів і комісій, що входять до вартості квитка, порівняння вартості проїзду в вагонах різного класу, вартість додаткових послуг (кава, постільна білизна, обід) у порівнянні з вартістю при купівлі в магазині, різниця вартості повного і пільгового квитків, вартість в залежності від дня тижня, коли відбудеться рейс, вартість різних потягів на одному і тому самому маршруті, економія;

рисунок 27. Квитки на потяг

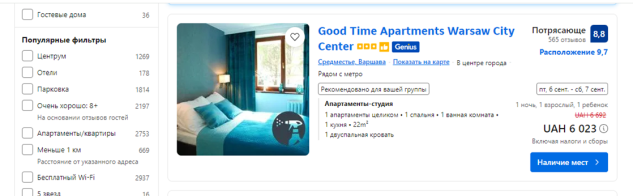
• бронювання готелю (рис.28): від яких параметрів і як у цифрах залежить вартість проживання в певному готелі, який відсоток знижок в гарячих пропозиціях, вартість додаткових послуг, як впливає на вартість зірковість готелю, як можна зекономити на типі номеру в одному і тому самому готелі, як впливає на вартість раннє бронювання;

рисунок 28. Бронювання готелю

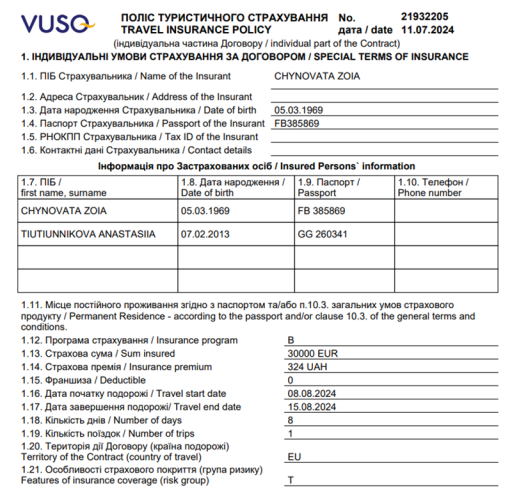
• страхування (рис.29): який відсоток від суми страхування пропонує турфірма, чи відрізняється ця платня у національний валюті та валюті країни для подорожі, у якій валюті вигідніше оформлювати страховий поліс;

рисунок 29. Поліс страхування

 

• трансфер: порівняти вартість трансферу від турфірми, таксі та міського транспорту;
• купівля у магазинах, супермаркетах (рис.30): курс валют, ціни в національній та іноземній валютах, різниця у розрахунках готівкою та карткою, чи є подвійна конвертація у безготівкових розрахунках; відсоток ПДВ;

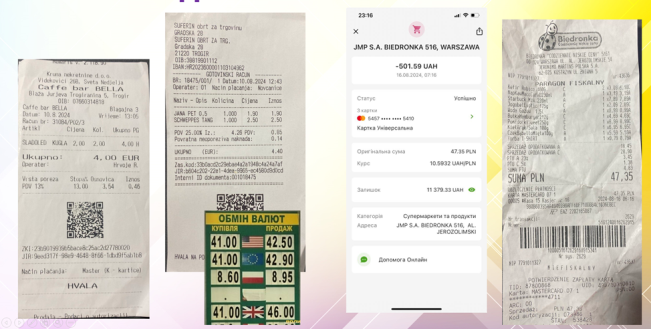
рисунок 30. Купівля в магазинах

• екскурсійний маршрут на гугл карті: оптимальний маршрут для знайомства із видатними пам’ятками – довжина маршруту, витрачений час, вартість проїзду;
• літак запізнився на 50 хв (рис.31): скільки часу тривав політ? О котрій годині був виліт? О котрій годині була посадка, якщо під час польоту запізнення скоротили на 20 хв? Яку частину години становить 50 хв? Скільки часу тривав політ із урахуванням запізнення? На скільки відсотків збільшився час польоту?

рисунок 31. Квиток на літак

 

ВИСНОВОК

Компетентнісно орієнтовані завдання є чудовим способом перевірки рівня сформованості предметних та загальних компетентностей. Але роллю контролю їхня функція не обмежується: вони неабияк мотивують на початку заняття. Крім того, такі завдання можуть стати захопливою вправою для групової роботи, а їхнє створення — чудовим навчальним проєктом, що сприятиме не лише вивченню нового матеріалу, а й закріпленню вже відомого.

Моделювання життєвих ситуацій на заняттях математики сприяє виявленню таких ознак предметної математичної компетентності учнів:

• цілісне сприйняття світу, розуміння ролі математики у пізнанні дійсності;
• розпізнавання проблем, які вирішуються із застосуванням математичних методів;
• здатність розв’язувати сюжетні задачі, логічно міркувати, виконувати дії за алгоритмом й складати алгоритм, обґрунтовувати свої дії;
• уміння користуватися математичною термінологією, знаковою і графічною інформацією;
• уміння орієнтуватися на площині та у просторі;
• здатність застосовувати обчислювальні навички й досвід вимірювання величин у практичних ситуаціях.

Важливу роль у формуванні компетентності студентів відіграє набуття ними у процесі моделювання життєвих і проблемних ситуацій досвіду задоволення пізнавальних інтересів, проявів емоційно-ціннісних ставлень, творчої активності, спілкування, соціальних орієнтація.

Виявлення інтересу та забезпечення успішного засвоєння навчального матеріалу суттєво впливає на підвищення рівня навчальних досягнень студентів, розвиток мислення, мовлення та кмітливості.